NLP基础 拼写纠错Spell Correction与文本表示Word Representation

NLP基础系列 （二）

---

一、拼写纠错Spell Correction

Find the words with smallest edit distance
编辑距离的定义是给定两个字符串str1和str2, 我们要计算通过最少多少代价cost可以把str1转换成str2.

举个例子：

输入: str1 = “geek”, str2 = “gesek” 输出: 1 插入 's’即可以把str1转换成str2

输入: str1 = “cat”, str2 = “cut” 输出: 1 用u去替换a即可以得到str2

输入: str1 = “sunday”, str2 = “saturday” 输出: 3

我们假定有三个不同的操作： 1. 插入新的字符 2. 替换字符 3. 删除一个字符。 每一个操作的代价为1.

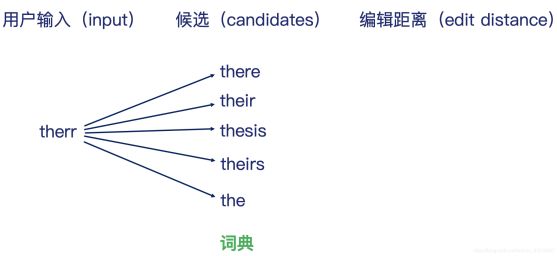
这里，我们要将用户的输入’therr‘ 纠正成正确的候选词需要多少edit distance：
there：cost 1，their：cost 1， thesis：cost 2，theirs：cost 2，the：cost 2
算出字典中所有的edit distance并取最小的结果，因此我们每次纠错都需要遍历整个词典，复杂度为O(n)

# 基于动态规划的解法
def edit_dist(str1, str2):
    
    # m，n分别字符串str1和str2的长度
    m, n = len(str1), len(str2)
    
    # 构建二位数组来存储子问题（sub-problem)的答案 
    dp = [[0 for x in range(n+1)] for x in range(m+1)] 
      
    # 利用动态规划算法，填充数组
    for i in range(m+1): 
        for j in range(n+1): 
  
            # 假设第一个字符串为空，则转换的代价为j (j次的插入)
            if i == 0: 
                dp[i][j] = j    
              
            # 同样的，假设第二个字符串为空，则转换的代价为i (i次的插入)
            elif j == 0:
                dp[i][j] = i
            
            # 如果最后一个字符相等，就不会产生代价
            elif str1[i-1] == str2[j-1]: 
                dp[i][j] = dp[i-1][j-1] 
  
            # 如果最后一个字符不一样，则考虑多种可能性，并且选择其中最小的值
            else: 
                dp[i][j] = 1 + min(dp[i][j-1],        # Insert 
                                   dp[i-1][j],        # Remove 
                                   dp[i-1][j-1])      # Replace 
  
    return dp[m][n] 

Better Way

def generate_edit_one(str):
    """
    给定一个字符串，生成编辑距离为1的字符串列表。
    """
    letters    = 'abcdefghijklmnopqrstuvwxyz'
    splits = [(str[:i], str[i:])for i in range(len(str)+1)]
    inserts = [L + c + R for L, R in splits for c in letters]
    deletes = [L + R[1:] for L, R in splits if R]
    replaces = [L + c + R[1:] for L, R in splits if R for c in letters]
    
    #return set(splits)
    return set(inserts + deletes + replaces)

print (len(generate_edit_one("apple")))

def generate_edit_two(str):
    """
    给定一个字符串，生成编辑距离不大于2的字符串
    """
    return [e2 for e1 in generate_edit_one(str) for e2 in generate_edit_one(e1)]

print (len(generate_edit_two("apple")))

How to Select? 如何过滤

其中P(s|c)是我们通过历史书籍获得的概率，例如
P(app|apple)即用户输入app但是最终用户想输入的单词为apple在历史数据中的记录
P©即通过语言模型获得的概率。

Words Filtering

Filtering Words
对于NLP的应⽤，我们通常先把停⽤词、出现频率很低的词汇过滤掉
这其实类似于特征筛选的过程
Removing Stop Words
在英⽂⾥，⽐如 “the”, “an”, “their”这些都可以作 为停⽤词来处理。但是，也需要考虑⾃⼰的应⽤场景
Low Frequency Words
出现频率特别低的词汇对分析作⽤不⼤，所以⼀般也 会去掉。把停⽤词、出现频率低的词过滤之后，即可 以得到⼀个我们的词典库。

Words Normalization

Stemming: one way to normalize
went, go, going 合并 = go
fly, flies,
deny, denied, denying
fast, faster, fastest
意思都类似，进行合并

https://tartarus.org/martin/PorterStemmer/java.txt

二、文本表示Word Representation

假设我们有一个词典： [我们，去，爬⼭，今天，你们，昨天，跑步]
用one-hot encoding每个单词的表示：
我们： [1, 0, 0, 0, 0, 0, 0 ]
爬⼭： [0, 0, 1, 0, 0, 0, 0 ]
跑步: [0, 0, 0, 0, 0, 0, 1 ]
昨天： [0, 0, 0, 0, 0, 1, 0 ]
那么，每个词的维度为7维，也就是整个词典的大小
我们用同样的方法来表示一个句子
Sentence Representation (boolean)
只要出现这个词就记为1，不管出现几次
词典： [我们，⼜，去，爬⼭，今天，你们，昨天，跑步]
每个句⼦的表示
我们 今天 去 爬⼭： [1, 0, 1, 1, 1, 0, 0, 0]
你们 昨天 跑步： [0, 0, 0, 0, 0, 1, 1, 1]
你们 ⼜ 去 爬⼭ ⼜ 去 跑步： [0, 1, 1, 1, 0, 1, 0, 1]
每个句子的维度为8维，也就是整个词典的大小
Sentence Representation (count)
把单词出现次数加入考虑
我们 今天 去 爬⼭： [1, 0, 1, 1, 1, 0, 0, 0]
你们 昨天 跑步： [0, 0, 0, 0, 0, 1, 1, 1]
你们 ⼜ 去 爬⼭ ⼜ 去 跑步： [0, 2, 2, 1, 0, 1, 0, 1]
计算Sentence Similarity
计算距离（欧式距离）： = | − |
计算相似度（余弦相似度）： = 点乘 / ( ｜｜ ∗｜ ｜ )

句⼦1：He is going from Beijing to Shanghai
句⼦2：He denied my request, but he actually lied.
句⼦3：Mike lost the phone, and phone was in the car
句⼦1： ( 0 , 0 , 1 , 0 , 0 , 0 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 1 , 0 )
句⼦2： ( 1 , 0 , 0 , 1 , 0 , 1 , 0 , 0 , 2 , 0 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 0 , 0 , 0 , 0)
其中denied没在字典中被记为0，而he出现2次记为2，但是在处理文本时，一些没有出现过的单词反而可能更重要。
并不是出现的越多就越重要！ 并不是出现的越少就越不重要！

from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
corpus = [
     'He is going from Beijing to Shanghai.',
     'He denied my request, but he actually lied.',
     'Mike lost the phone, and phone was in the car.',
]
X = vectorizer.fit_transform(corpus)
print (X.toarray())
print (vectorizer.get_feature_names())

[[0 0 1 0 0 0 1 1 1 0 1 0 0 0 0 0 0 1 0 1 0]
 [1 0 0 1 0 1 0 0 2 0 0 1 0 0 1 0 1 0 0 0 0]
 [0 1 0 0 1 0 0 0 0 1 0 0 1 1 0 2 0 0 2 0 1]]
['actually', 'and', 'beijing', 'but', 'car', 'denied', 'from', 'going', 'he', 'in', 'is', 'lied', 'lost', 'mike', 'my', 'phone', 'request', 'shanghai', 'the', 'to', 'was']

那么，我们需要考虑单词的重要性：

Tf-idf Representation

idf算法考虑了单词的重要性，往往出现越多次的单词往往没有那么重要。
词典： [我们，⼜，去，爬⼭，今天，你们，昨天，跑步] dim = 8
以下3个文本：
我们 今天 去 爬⼭
你们 昨天 跑步
你们 ⼜ 去 爬⼭ ⼜ 去 跑步

则 我们 今天 去 爬⼭： [1✖️log(1/3), 0, 1✖️log(2/3), 1✖️log(2/3), 1✖️log(1/3), 0, 0, 0]
代码实现：

from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(smooth_idf=False)
X = vectorizer.fit_transform(corpus)
print (X.toarray())

[[0.         0.         0.39379499 0.         0.         0.
  0.39379499 0.39379499 0.26372909 0.         0.39379499 0.
  0.         0.         0.         0.         0.         0.39379499
  0.         0.39379499 0.        ]
 [0.35819397 0.         0.         0.35819397 0.         0.35819397
  0.         0.         0.47977335 0.         0.         0.35819397
  0.         0.         0.35819397 0.         0.35819397 0.
  0.         0.         0.        ]
 [0.         0.26726124 0.         0.         0.26726124 0.
  0.         0.         0.         0.26726124 0.         0.
  0.26726124 0.26726124 0.         0.53452248 0.         0.
  0.53452248 0.         0.26726124]]

Measure Similarity Between Words

下⾯哪些单词之间语义相似度更⾼？
我们： [1, 0, 0, 0, 0, 0, 0]
爬⼭： [0, 0, 1, 0, 0, 0, 0]
运动: [0, 0, 0, 0, 0, 0, 1]
昨天： [0, 0, 0, 0, 0, 1, 0]
显然我们无法使用One-hot 表示法表达单词之间相似度，因为不管计算euclidean distance还是cosine similarity 他们结果都相同
还有一个问题，即每个单词的向量表示中只有一个位置上是1其他都为0
Another Issue: Sparsity
因此One-hot encoding 无法表示语义的相似度以及过度稀疏性。

From One-hot Representation to Distributed Representation

我们使用分布式表示方法来表示单词，也就是词向量（word Vec）

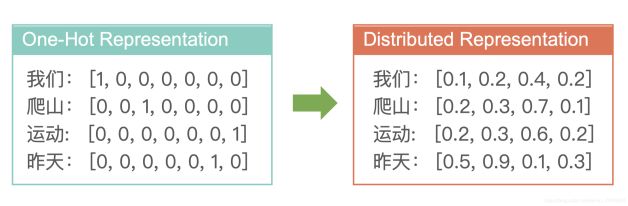
很显然，通过语言模型LM计算好的Distributed Representation可以有效的使用euclidean distance或者cosine similarity来计算单词之间的语义相似度
Comparing the Capacities
Q: 100 维的 One-Hot 表示法最多可以表达多少个不 同的单词？
只能表示100个单词
Q: 100 维的 分布式 表示法最多可以表达多少个不 同的单词？
假设服从二项分布binary distribution，那么100维可以表示2^100个单词

Word Embeddings

我们输入的是string，通过深度学习模型来生成Distributed Representation
常见的word embedding模型有：Skip- gram，Glone，CBow，RNN/LSTM 等等
通常来说，我们生成的词向量已经包含了每个单词代表的意义meaning
我们也可以通过降维来实现可视化：

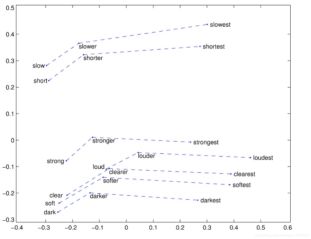
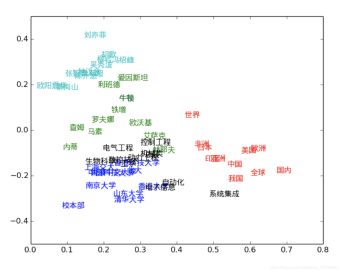
From Word Embedding to Sentence Embedding

• Average 法则，即把句子中所有词向量相加取平均
• LSTM/RNN来实现