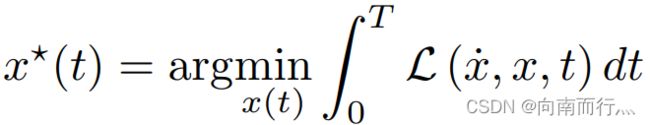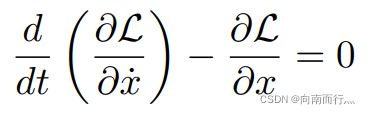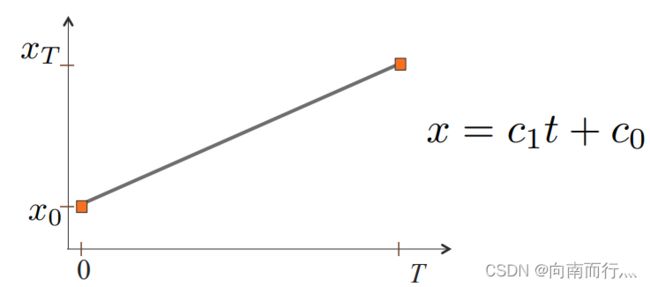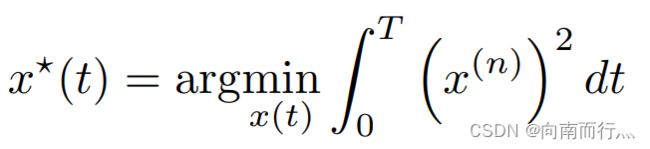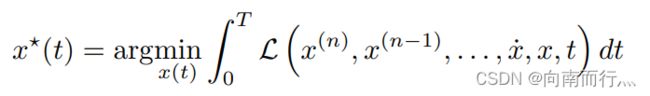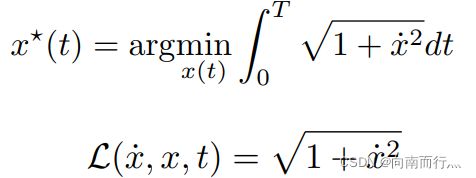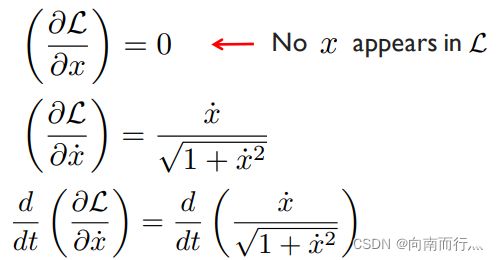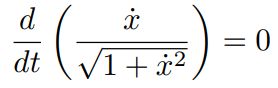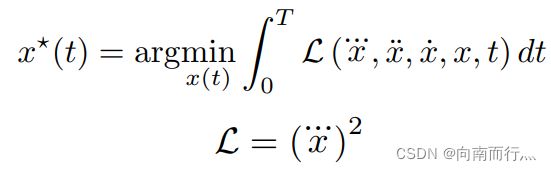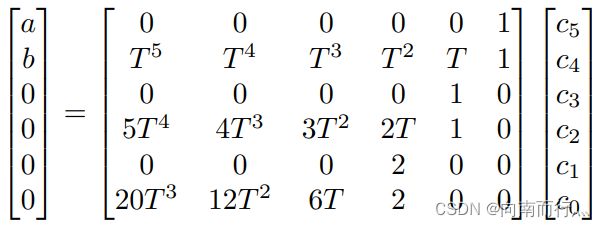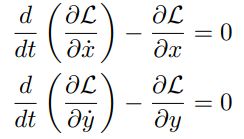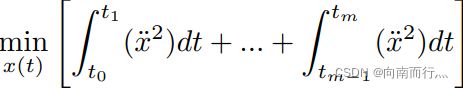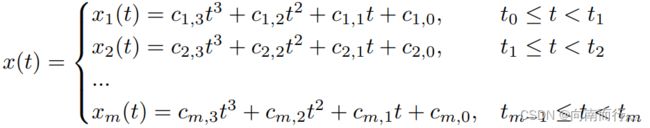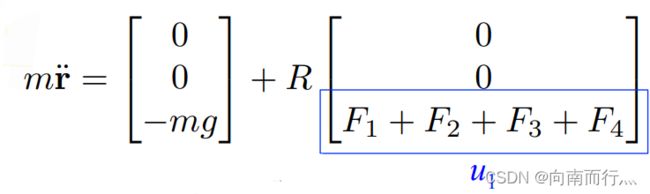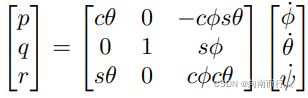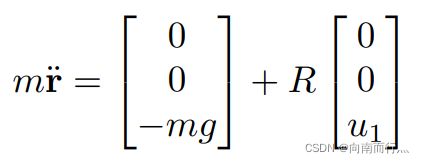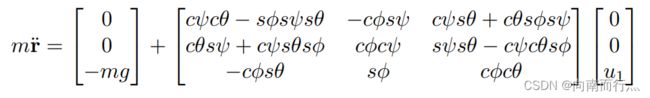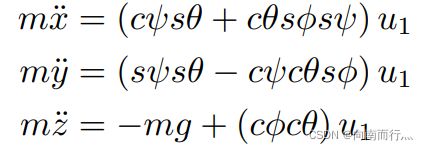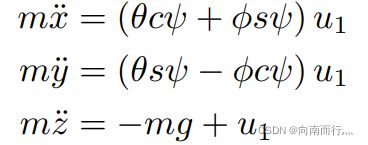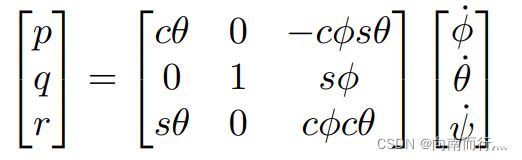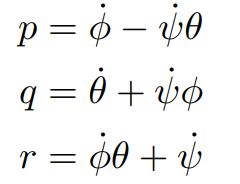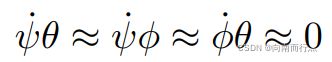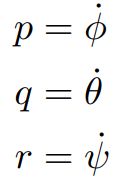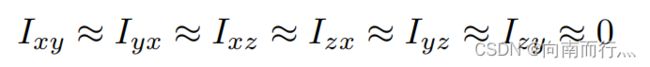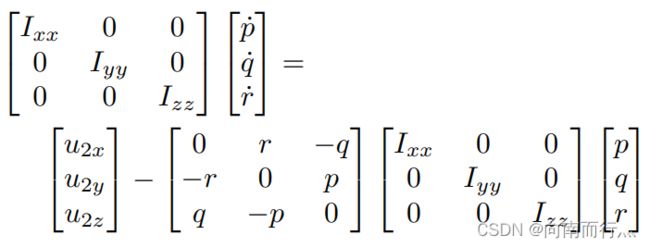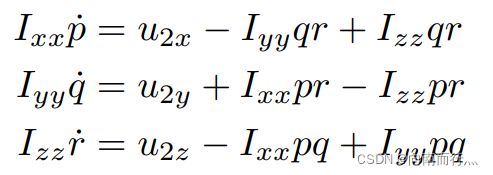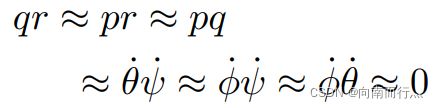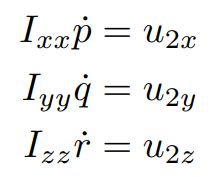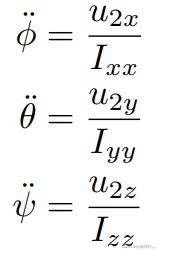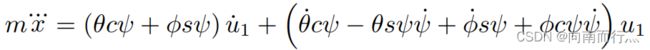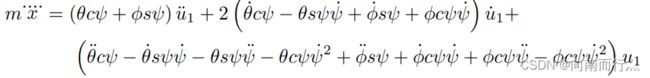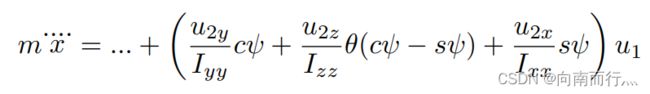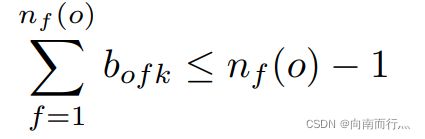Robotics: Aerial Robotics(空中机器人)笔记(六):无人机运动规划
在之前的学习中我们已经讨论了如何根据给定轨迹对四旋翼进行控制,在这一章里,我们将探索四旋翼无人机在三维空间中的运动规划,即给定一个三维的环境,我们希望能够在这个三维环境中指定具体的点,进而让四旋翼无人机在这个环境中规划出无障碍的轨迹路线。
上一章链接:
Robotics: Aerial Robotics(空中机器人)笔记(五):无人机在二维平面以及三维空间中的PD运动控制
时间、运动和轨迹(Time, Motion and Trajectories)
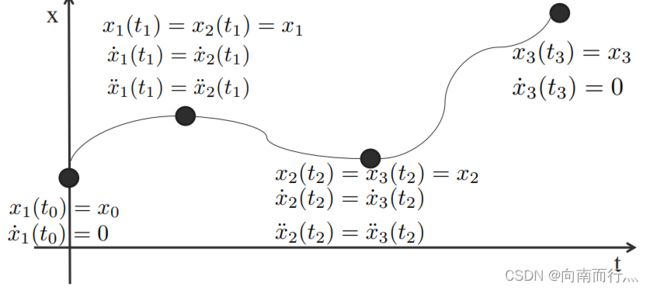
首先我们先考虑相对简单的子问题,其描述如下,假设目标是某刚体,该目标需要从起始位置移动到目标位置(我们也会关注其运动的方向),且在这个问题中, ,刚体可能需要经过一些中间位置:
由于四旋翼无人机是一个动力学系统,也就是其运动状态是没办法突变的(例如速度没办法从1 m/s突变到3 m/s,需要有一个加速度),所以四旋翼无人机的轨迹是需要光滑的,这一要求常常被转化为最小化输入的变化率,我们将在后续继续讨论这个问题。
我们会特别关注动力学系统的阶数,如果用运动学模型来考虑某机器人,也就是说我们可以任意指定速度的话,这就是一个一阶系统。如果是二阶动力学的机器人,这意味着可以任意指定加速度,对于三阶系统的话对应的是加速度的导数,称之为 jerk,四阶就是 jerk 的导数 snap,系统的阶数将决定输入的类别,如果是 n 阶系统,就是在指定位置 (惯性系坐标)的第 n 阶导数。
欧拉-拉格朗日方程(Euler-Lagrange Equation)
一般来说,从一阶到 n-1 阶导数都有相应的边界条件,为了解决这个问题我们将使用变分法(Calculus of variations)这一工具。如下式所示,![]() 称之为泛函数,泛函数是函数的函数,即它的输入是函数,输出是实数,而这个输出值取决于一个或多个函数(输入)在一整个路径上的积分,
称之为泛函数,泛函数是函数的函数,即它的输入是函数,输出是实数,而这个输出值取决于一个或多个函数(输入)在一整个路径上的积分,![]() 是一个被积的函数。变分法的目标是通过选择被积函数来最大化或最小化泛函数的值,这里我们是用来最小化
是一个被积的函数。变分法的目标是通过选择被积函数来最大化或最小化泛函数的值,这里我们是用来最小化 ![]() 的值,即使其取极小值:
的值,即使其取极小值:
当泛函数取极值时,被积函数应当满足欧拉-拉格朗日方程,欧拉-拉格朗日方程包括被积函数对 ![]() 和
和 ![]() 的偏微分项和以及对时间
的偏微分项和以及对时间 ![]() 的全微分项:
的全微分项:
其详细证明可以在以下链接找到,这里就不多做解释了:
【变分计算1】欧拉-拉格朗日方程
求解光滑轨迹(Smooth Trajectories)
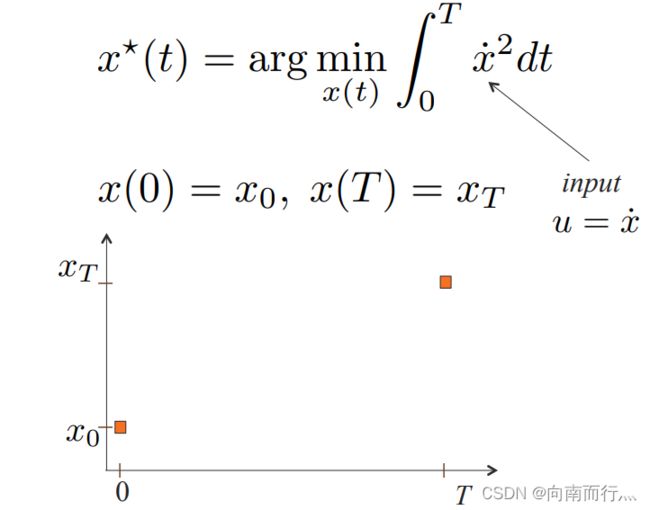
我们来考虑一个欧拉-拉格朗日方程的最简单的应用,考虑一个一阶的系统,即输入的是位置的一阶导数(速度),指定在时间 ![]() 的时候的位置是
的时候的位置是 ![]() ,时间
,时间 ![]() 的时候的位置是
的时候的位置是 ![]() ,目标是让速度的平方经过整个轨迹的积分最小。
,目标是让速度的平方经过整个轨迹的积分最小。
如果我们采用欧拉-拉格朗日方程,让函数 ![]() 为速度的平方,那么欧拉-拉格朗日方程中第一项对
为速度的平方,那么欧拉-拉格朗日方程中第一项对 ![]() 微分后就是
微分后就是 ![]() ,其再对时间微分就是
,其再对时间微分就是 ![]() ,而第二项为0,这是因为函数
,而第二项为0,这是因为函数 ![]() 中只有
中只有 ![]() 而没有
而没有 ![]() ,就有:
,就有:
我们对其积分,可知其速度是一个常数:
再对速度积分就能得到下式,此时我们再把之前说的边界条件代入进去,就能得到一条确切的直线了:
这种情况就是前面我们提到的一阶系统,相应的输入是速度,它适用于使用运动学模型的机器人。一般来说,系统可能具有更高阶的动态特征,例如,对于某 n 阶系统,你可能无法做到指定某个速度 因为系统具有惯性,对于 n 阶系统,输入是位置的 n 阶导数:
对于欧拉-拉格朗日方程来说,高阶的系统也会相应复杂一些,也包含相应的偏微分项和全微分项:
如果阶数为1,我们就能得到最小速度轨迹,同时也是最短轨迹长度。阶数为2时,得到的是最小加速度轨迹。由此可得,阶数为3是最小jerk轨迹,阶数为4是最小snap轨迹。
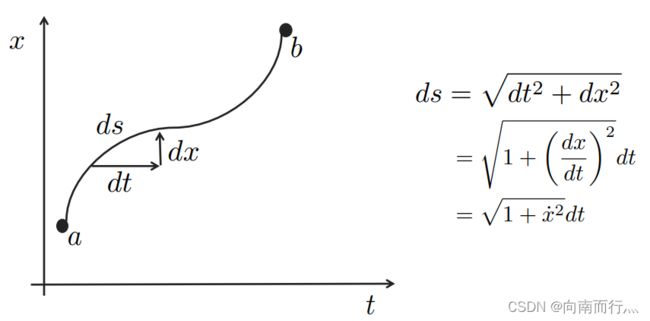
接下来我们来思考一下为什么阶数为1时得到的是最短轨迹长度,我们来看任意两点之间的轨迹,可以把轨迹微分成很多段,每一段长度为ds,那么就能得到ds的表达式:
轨迹的总长度就是:
我们的目标就是最小化轨迹的长度,那么我们就可以用欧拉-拉格朗日方程了:
所以就可以得到:
事实上我们并不需要把这个微分项求出来,我们对其积分可知,其是一个常数 ![]() ,那么我们就可以反解出
,那么我们就可以反解出 ![]() ,其事实上也是一个常数:
,其事实上也是一个常数:
那么我们再对其积分,就能得到我们最小速度轨迹对应的函数:
所以说如果阶数为1,我们就能得到最小速度轨迹,同时也是最短轨迹长度。
最小 Jerk 轨迹(Minimum Jerk Trajectory)
接下来我们慢慢扩展,首先我们考虑如何得到最小jerk轨迹,也就是:
运用欧拉-拉格朗日方程我们就可以得到:
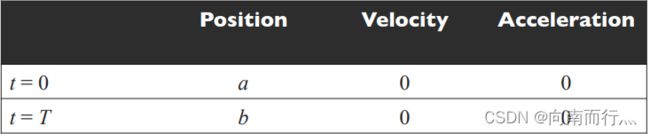
我们通过边界条件就可以得到,通过 ![]() 就能得到下式:
就能得到下式:
之后我们来看多个维度的情况,假设现在一阶系统的轨迹是二维的,那么我们就有:
这时就有两个欧拉-拉格朗日方程:
那么就能得到两个一阶微分方程,通过求解就能得到轨迹在两个维度的分量。
路点导航(Waypoint Navigation)
在机器人学中,仅仅指定起始和终点的位姿并不够,我们在中间的位姿往往也要考虑,假设我们已经得到了一组需要通过的点:
那么机器人的轨迹绝对不是简单地把两个点之间用直线连接起来,原因是机器人往往是动力学系统,具有惯性,不可能在位置点急转弯,所以轨迹需要平滑。我们考虑求二阶系统的最小加速度曲线。
三次样条(Cubic Spline)
我们知道,现在轨迹被分成了多段,那么轨迹就是这多段连接起来:
那么我们在每段应用欧拉-拉格朗日方程,就可以得到每一段的函数式,这个函数就称之为三次样条:
我们看到,每一段有4个常数需要知道,那么这个三次样条有m段,就有4m个常数要求解。
接下来我们就要通过边界条件来求这些,有m段轨迹,那么就有轨迹上有m+1个点,中间的点关于位置的方程每个有两个约束(![]() ),所以有
),所以有 ![]() 个约束,再加上我们定义初始和终点两个点的位置已知,就有2m个式子。接下来我们看每个点上的加速度约束和jerk约束,在每个点上要保持连续,所以总共就有
个约束,再加上我们定义初始和终点两个点的位置已知,就有2m个式子。接下来我们看每个点上的加速度约束和jerk约束,在每个点上要保持连续,所以总共就有 ![]() 个约束,最后我们定义在初始和终点两个点的加速度为0就有总共4m个约束了,就可以解出4m个常数。
个约束,最后我们定义在初始和终点两个点的加速度为0就有总共4m个约束了,就可以解出4m个常数。
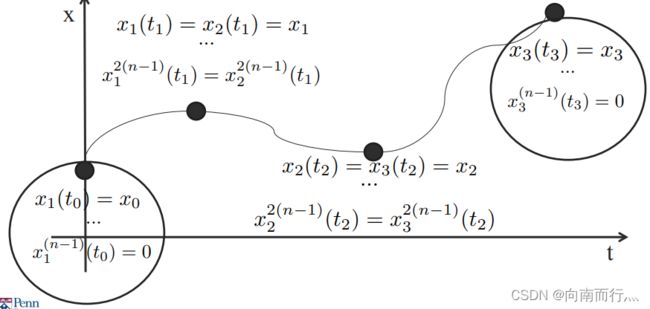
这个基本思想可以推广到n阶系统:
我们必须在起点和终点时指定适当的边界条件,同时还要指定中间边界条件, 这些中间边界条件定义了2(n-1)个导数的连续性。
四旋翼无人机的运动规划(Motion Planning for Quadrotors)
我们现在可以将我们之前学习的内容运用到四旋翼无人机上了,回想一下,四旋翼无人机的控制器包含两个回路,一个是外部的位置控制回路,其决定了 ![]() ,一个是内部的姿态控制回路,其决定了
,一个是内部的姿态控制回路,其决定了 ![]() :
:
再回顾下我们之前学习的几个方程,在第一个方程中我们可以看出位置的二阶导数由 ![]() 决定,它是一个标量,但能控制加速度在xyz上的分量,第二个方程将角速度pqr和三个姿态角联系了起来,第三个方程将
决定,它是一个标量,但能控制加速度在xyz上的分量,第二个方程将角速度pqr和三个姿态角联系了起来,第三个方程将 ![]() 与角速度的变化率联系了起来。因为旋转矩阵R是关于
与角速度的变化率联系了起来。因为旋转矩阵R是关于 ![]() 的函数,所以由最下面的两个方程可以看出,旋转矩阵的二阶导数由
的函数,所以由最下面的两个方程可以看出,旋转矩阵的二阶导数由 ![]() 决定。从第一个方程我们可以看到位置的二阶导数(加速度)与输入
决定。从第一个方程我们可以看到位置的二阶导数(加速度)与输入 ![]() 线性相关,通过考虑旋转矩阵R与
线性相关,通过考虑旋转矩阵R与 ![]() 的相关性,我们可以将其结合表明位置的四阶导数取决于
的相关性,我们可以将其结合表明位置的四阶导数取决于 ![]() 。
。
接下来我们将通过线性化模型来证明这一点,同时我们将会发现:
1. 角速度通过单位矩阵和三个姿态角相关。
2. 最下面方程中的非线性惯性依赖项则会消失。
线性化模型(Linearized Model)
我们假设四旋翼无人机处在临界悬停状态,那么此时就有:
线性化模型中我们可以作以下替换,因为 ![]() 和
和 ![]() 趋近于0的,由高等数学中极限的相关知识就可以得到:
趋近于0的,由高等数学中极限的相关知识就可以得到:
我们由第一个方程:
并将ZXY欧拉角对应的旋转矩阵代入进去就可以得到:
这里需要注意的是,如果我们在线性化模型的时候把偏航角 ![]() 也近似为0的话,那么此时的旋转矩阵R就是单位矩阵。
也近似为0的话,那么此时的旋转矩阵R就是单位矩阵。
通过线性替换得出下式,所以我们就可以得到位置的二阶导数(加速度)与输入 ![]() 成正比。
成正比。
接下来我们来看角速度分量 p 、q 、 r和欧拉角一阶导数之间的关系:
将其线性替换就可以得到:
又因为姿态角和其一阶导数都是接近0的项,所以我们可以把它们的相乘项都近似成0:
那么就有下式,也就证明了第一个结论,角速度通过单位矩阵和三个姿态角相关:
接下来我们来看最后一个方程,我们将惯性矩阵上的惯性项近似为0:
就有:
又因为之前我们推导过的pqr的值其实也是接近于0的项,所以其相乘也都近似成0:
我们就得到了如下式所示,也就是说原先方程中的非线性惯性依赖项已经消失了:
我们再把p、q和r用先前推导过的姿态角替换回去,就得到姿态角的二阶导与输入 ![]() 的关系:
的关系:
我们再回去看加速度与 ![]() 的方程,以x上的分量为例:
的方程,以x上的分量为例:
对其求两次导,得到位置的四阶导方程:
我们把姿态角的二阶导与输入 ![]() 相关的方程代入进去,省略掉前面不相关的项,我们专注看后面的:
相关的方程代入进去,省略掉前面不相关的项,我们专注看后面的:
那么我们就得到了位置的四阶导数与 ![]() 成正比这一结论。
成正比这一结论。
障碍物(Obstacles)
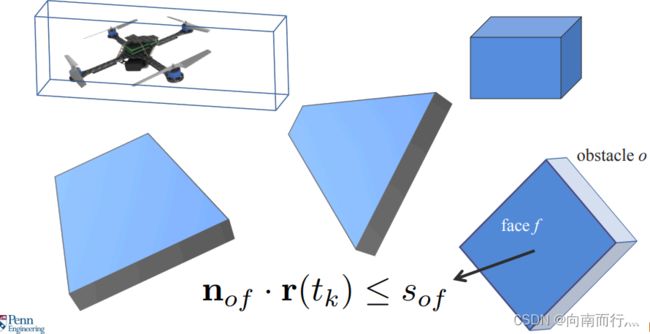
我们之前已经讨论过了无障碍物下如何生成轨迹,接下来我们要考虑障碍物的存在。我们把无人机装在虚拟矩形框中并假设这些矩形已知,每个障碍物都是凸的,通过多面体模型可以表征每个障碍物的范围。我们从表征无人机的矩形以及障碍物每个面来研究碰撞, 对于时间为 ![]() 时障碍物 o 上的面 f,我们要确保表征机器人的凸多面体的位置
时障碍物 o 上的面 f,我们要确保表征机器人的凸多面体的位置 ![]() 和面 f 不要相交,也就是要满足如下的表达式:
和面 f 不要相交,也就是要满足如下的表达式:
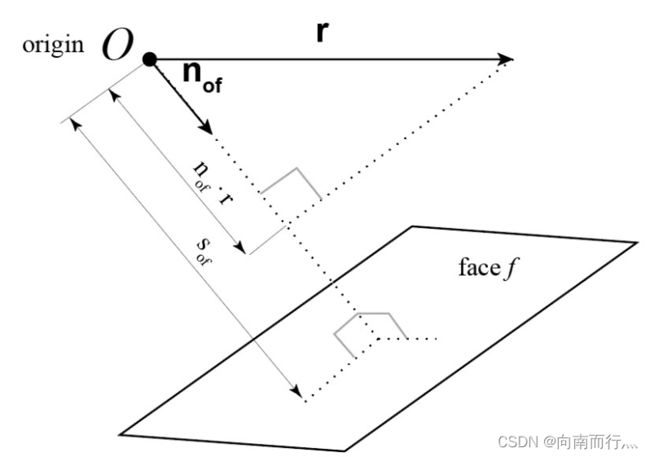
其中,![]() 表示的是面f的内向法向量,为什么这样的不等式就能保证无人机与障碍物的面不会碰撞,其示意图就如下所示,不等式约束了机器人可以到达的位置:
表示的是面f的内向法向量,为什么这样的不等式就能保证无人机与障碍物的面不会碰撞,其示意图就如下所示,不等式约束了机器人可以到达的位置:
我们可以在每个时刻,对于每个障碍物都可以写下类似的不等式,应当注意的是,这里相比于之前的不等式多了一个额外项,由一个非常大的正常数M和一个二元变量B组成:
这是因为如果机器人与障碍物发生碰撞时,障碍物所有的面的不等式才都不成立,也就是说,避免发生碰撞时都得满足所有的面的不等式。如果只是其中一些面不满足,不能认为机器人与障碍物发生了碰撞。也就是如果有障碍物有 ![]() 个面,那么我们就要保证至少有一个二元变量为0才不会发生碰撞,这是因为如果所有的
个面,那么我们就要保证至少有一个二元变量为0才不会发生碰撞,这是因为如果所有的 ![]() 都为1的话,意味着所有的面都得加上这个很大的项才能满足不等式,也就是发生了碰撞:
都为1的话,意味着所有的面都得加上这个很大的项才能满足不等式,也就是发生了碰撞:
下一章链接:
Robotics: Aerial Robotics(空中机器人)笔记(完):无人机的非线性控制