吴恩达机器学习ex3-neural network python版

机器学习练习 3 - 多类分类

对于此练习，我们将使用逻辑回归来识别手写数字（0到9）。 我们将扩展我们在练习2中写的逻辑回归的实现，并将其应用于一对一的分类。 让我们开始加载数据集。 它是在MATLAB的本机格式，所以要加载它在Python，我们需要使用一个SciPy工具。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
data = loadmat('ex3data1.mat')#mat文件是matlab的数据存储的标准格式
data

{‘header’: b’MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Oct 16 13:09:09 2011’,
‘version’: ‘1.0’,
‘globals’: [],
‘X’: array([[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.],
…,
[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.]]),
‘y’: array([[10],
[10],
[10],
…,
[ 9],
[ 9],
[ 9]], dtype=uint8)}

data['X'].shape, data['y'].shape

((5000, 400), (5000, 1))

好的，我们已经加载了我们的数据。图像在martix X中表示为400维向量（其中有5,000个）。 400维“特征”是原始20 x 20图像中每个像素的灰度强度。类标签在向量y中作为表示图像中数字的数字类。

第一个任务是将我们的逻辑回归实现修改为完全向量化（即没有“for”循环）。这是因为向量化代码除了简洁外，还能够利用线性代数优化，并且通常比迭代代码快得多。但是，如果从练习2中看到我们的代价函数已经完全向量化实现了，所以我们可以在这里重复使用相同的实现。

sigmoid 函数

g 代表一个常用的逻辑函数（logistic function）为S形函数（Sigmoid function），公式为：
()=1/1+−
合起来，我们得到逻辑回归模型的假设函数：
ℎ()=1/1+−

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

代价函数： ()=1∑=1[−()log(ℎ(()))−(1−())log(1−ℎ(()))]

def cost2(theta,X,y,learningRate):
    X=np.matrix(X)
    y=np.matrix(y)
    theta=np.matrix(theta)
    m=len(X)
    
    first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
    second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
    zhengze=learningRate*np.sum(np.power((theta[:,1:]),2))
    
    j=(1/m)*(np.sum(first)-np.sum(second))+zhengze/(2*m)
    
    return j
​
def cost(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对0 进行正则化，所以梯度下降算法将分两种情形：

{
0:=0−1∑=1[ℎ(())−()]()0 :=−1∑=1[ℎ(())−()]()+
}

以下是原始代码是使用for循环的梯度函数：

def gradient_with_loop2(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = theta.shape[1]
    grad = np.matrix(np.zeros(theta.shape[1]))
    
    for i in range(parameters):
        if (i == 0):
            grad[i] = np.sum((sigmoid(X * theta.T) - y)*X[:,i]) / len(X)
        else:
            grad[i] = (np.sum((sigmoid(X * theta.T) - y)*X[:,i]) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    
    return grad
​
​
def gradient_with_loop(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    
    return grad

向量化的梯度函数

​

def gradient2(theta, X, y, learningRate):#theta 第一列为1
    theta=np.matrix(theta)
    X=np.matrix(X)
    y=np.matrix(y)
    
    temp=np.matrix(np.zeros(theta.shape[1]))
    error = sigmoid(X * theta.T) - y
    temp=error.T*X/len(X)+learningRate/len(X)*theta#这里要注意没有求和了，因为在矩阵做乘法的过程中已经把行求得的积相加了，以后看见求和要注意一下
    temp[0,0]=np.sum(np.multiply((sigmoid(X*theta.T)-y),X[:,0]))/len(X)
​
    return temp
​
def gradient(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    error = sigmoid(X * theta.T) - y
    
    grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)
    
    # intercept gradient is not regularized
    grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)
    
    return np.array(grad).ravel()

现在我们已经定义了代价函数和梯度函数，现在是构建分类器的时候了。 对于这个任务，我们有10个可能的类，并且由于逻辑回归只能一次在2个类之间进行分类，我们需要多类分类的策略。 在本练习中，我们的任务是实现一对一全分类方法，其中具有k个不同类的标签就有k个分类器，每个分类器在“类别 i”和“不是 i”之间决定。 我们将把分类器训练包含在一个函数中，该函数计算10个分类器中的每个分类器的最终权重，并将权重返回为k X（n + 1）数组，其中n是参数数量。

from scipy.optimize import minimize
​
def one_vs_all(X, y, num_labels, learning_rate):#相当于把k个标签分开测试，每次循环计算一个标签的最优结果，保存起来
    rows = X.shape[0]#5000行数据
    params = X.shape[1]#400个特征
    
    # k X (n + 1) array for the parameters of each of the k classifiers
    all_theta = np.zeros((num_labels, params + 1))#权重返回为k *（n + 1）数组 相当于k个0/1判断器 长度为特征的长度401，初始特征为400，+1为后面要给X多增加的一列1，theta也要多一列
    
    # insert a column of ones at the beginning for the intercept term
    X = np.insert(X, 0, values=np.ones(rows), axis=1)#给X添加一列1
    
    # labels are 1-indexed instead of 0-indexed
    for i in range(1, num_labels + 1):
        theta = np.zeros(params + 1)
        y_i = np.array([1 if label == i else 0 for label in y])#逐一检查y中的行，如果行为当前想要的值，则赋1
        y_i = np.reshape(y_i, (rows, 1))#将y_i转换维度成（5000,1）
        
        # minimize the objective function
        fmin = minimize(fun=cost2, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=gradient2)
        all_theta[i-1,:] = fmin.x
    
    return all_theta

这里需要注意的几点：首先，我们为theta添加了一个额外的参数（与训练数据一列），以计算截距项（常数项）。 其次，我们将y从类标签转换为每个分类器的二进制值（要么是类i，要么不是类i）。 最后，我们使用SciPy的较新优化API来最小化每个分类器的代价函数。 如果指定的话，API将采用目标函数，初始参数集，优化方法和jacobian（渐变）函数。 然后将优化程序找到的参数分配给参数数组。

实现向量化代码的一个更具挑战性的部分是正确地写入所有的矩阵，保证维度正确。

#这里只是模拟一下要用到的数据的参数，下面真正用到函数的时候用的X，theta都是最原始的，所以在函数里也添加了列
rows = data['X'].shape[0]
params = data['X'].shape[1]
​
all_theta = np.zeros((10, params + 1))
​
X = np.insert(data['X'], 0, values=np.ones(rows), axis=1)#插入值为1的一列
​
theta = np.zeros(params + 1)
​
y_0 = np.array([1 if label == 0 else 0 for label in data['y']])
y_0 = np.reshape(y_0, (rows, 1))
​
X.shape, y_0.shape, theta.shape, all_theta.shape

​
((5000, 401), (5000, 1), (401,), (10, 401))

注意，theta是一维数组，因此当它被转换为计算梯度的代码中的矩阵时，它变为（1×401）矩阵。 我们还检查y中的类标签，以确保它们看起来像我们想象的一致。

np.unique(data['y'])#看下有几类标签

array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=uint8)

让我们确保我们的训练函数正确运行，并且得到合理的输出。

all_theta = one_vs_all(data['X'], data['y'], 10, 1)
all_theta

array([[-2.38319441e+00, 0.00000000e+00, 0.00000000e+00, …,
1.30442256e-03, -7.52260392e-10, 0.00000000e+00],
[-3.18457178e+00, 0.00000000e+00, 0.00000000e+00, …,
4.46157319e-03, -5.08676164e-04, 0.00000000e+00],
[-4.79802923e+00, 0.00000000e+00, 0.00000000e+00, …,
-2.86818378e-05, -2.47109741e-07, 0.00000000e+00],
…,
[-7.98688043e+00, 0.00000000e+00, 0.00000000e+00, …,
-8.96395481e-05, 7.23065705e-06, 0.00000000e+00],
[-4.57271816e+00, 0.00000000e+00, 0.00000000e+00, …,
-1.33059832e-03, 9.95893529e-05, 0.00000000e+00],
[-5.40510030e+00, 0.00000000e+00, 0.00000000e+00, …,
-1.16593193e-04, 7.88108976e-06, 0.00000000e+00]])

我们现在准备好最后一步 - 使用训练完毕的分类器预测每个图像的标签。 对于这一步，我们将计算每个类的类概率，对于每个训练样本（使用当然的向量化代码），并将输出类标签为具有最高概率的类。

def predict_all(X, all_theta):
    rows = X.shape[0]
    params = X.shape[1]
    num_labels = all_theta.shape[0]
    
    # same as before, insert ones to match the shape
    X = np.insert(X, 0, values=np.ones(rows), axis=1)
    
    # convert to matrices
    X = np.matrix(X)
    all_theta = np.matrix(all_theta)
    
    # compute the class probability for each class on each training instance
    h = sigmoid(X * all_theta.T)#计算出来所有预测值，每行（每个数据）找到预测值最大的列（最可能的分类编号）
    
    # create array of the index with the maximum probability
    h_argmax = np.argmax(h, axis=1)#np.argmax()找到列中数值最大的元素 返回元素索引
    
    # because our array was zero-indexed we need to add one for the true label prediction
    h_argmax = h_argmax + 1
    
    return h_argmax

现在我们可以使用predict_all函数为每个实例生成类预测，看看我们的分类器是如何工作的。

y_pred = predict_all(data['X'], all_theta)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, data['y'])]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print ('accuracy = {0}%'.format(accuracy * 100))

accuracy = 94.46%
在下一个练习中，我们将介绍如何从头开始实现前馈神经网络。

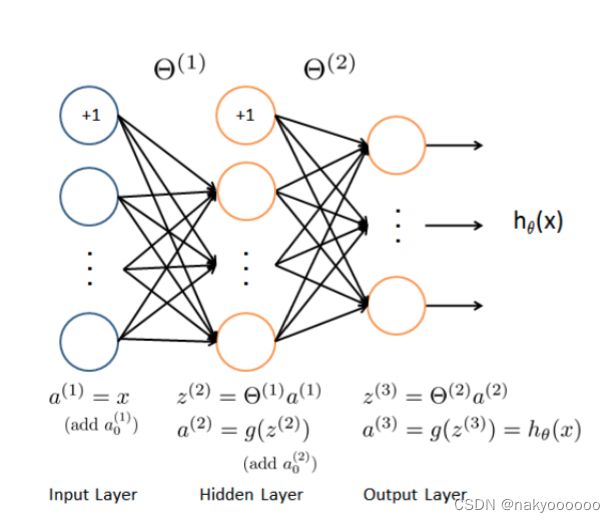
神经网络模型图示

#根据网络机器学习作业题添加
​
​
# 在前面一个部分，我们已经实现了多分类逻辑回归来识别手写数字。但是，逻辑回归并不能承载更复杂的假设，因为他就是个线性分类器。
# 这部分，你需要实现一个可以识别手写数字的神经网络。
# 神经网络可以表示一些非线性复杂的模型。权重已经预先训练好，你的目标是在现有权重基础上，实现前馈神经网络。
​
# 输入是图片的像素值，20*20像素的图片有400个输入层单元，不包括需要额外添加的加上常数项。
# 材料已经提供了训练好的神经网络的参数theta1、theta2，有25个隐层单元和10个输出单元（10个输出）
​
# 你需要实现前馈神经网络预测手写数字的功能。和之前的一对多分类一样，神经网络的预测会把theta(x)中值最大的，作为预测输出

weight = loadmat('ex3weights.mat')
# weight
theta1, theta2 = weight['Theta1'], weight['Theta2']
theta1.shape, theta2.shape#theta_i的维度为（i层的神经元个数，i-1层神经元个数），可以通过X的维度和 X*theta.T来换算

((25, 401), (10, 26))

# 插入常数项
X2 = np.matrix(np.insert(data['X'], 0, values=np.ones(X.shape[0]), axis=1))#输入还是上面的X 插入后的维度为（5000,401）
#X2 = np.matrix(np.insert(data['X'], 0, values=1, axis=1))
y2 = np.matrix(data['y'])
X2.shape, y2.shape

((5000, 401), (5000, 1))

a1 = X2
z2 = a1 * theta1.T
z2.shape

(5000, 25)

a2 = sigmoid(z2)
a2.shape

(5000, 25)

a2 = np.insert(a2, 0, values=np.ones(a2.shape[0]), axis=1)
#a2 = np.insert(a2, 0, values=1, axis=1)
z3 = a2 * theta2.T
z3.shape

(5000, 10)

a3 = sigmoid(z3)
a3#a3的维度，即输出的维度为(5000,10)，每个样本都有10个预测值（分别对应0-9），令预测值最大的那个当作最后的预测结果，即将预测值设为最大值的索引

matrix([[1.12661530e-04, 1.74127856e-03, 2.52696959e-03, …,
4.01468105e-04, 6.48072305e-03, 9.95734012e-01],
[4.79026796e-04, 2.41495958e-03, 3.44755685e-03, …,
2.39107046e-03, 1.97025086e-03, 9.95696931e-01],
[8.85702310e-05, 3.24266731e-03, 2.55419797e-02, …,
6.22892325e-02, 5.49803551e-03, 9.28008397e-01],
…,
[5.17641791e-02, 3.81715020e-03, 2.96297510e-02, …,
2.15667361e-03, 6.49826950e-01, 2.42384687e-05],
[8.30631310e-04, 6.22003774e-04, 3.14518512e-04, …,
1.19366192e-02, 9.71410499e-01, 2.06173648e-04],
[4.81465717e-05, 4.58821829e-04, 2.15146201e-05, …,
5.73434571e-03, 6.96288990e-01, 8.18576980e-02]])

y_pred2 = np.argmax(a3, axis=1) + 1
y_pred2.shape

(5000, 1)

from sklearn.metrics import classification_report
print(classification_report(y2, y_pred))

          precision    recall  f1-score   support

       1       0.95      0.99      0.97       500
       2       0.95      0.92      0.93       500
       3       0.95      0.91      0.93       500
       4       0.95      0.95      0.95       500
       5       0.92      0.92      0.92       500
       6       0.97      0.98      0.97       500
       7       0.95      0.95      0.95       500
       8       0.93      0.92      0.92       500
       9       0.92      0.92      0.92       500
      10       0.97      0.99      0.98       500
      
  accuracy                         0.94      5000
  macro avg    0.94      0.94      0.94      5000
  weighted avg 0.94      0.94      0.94      5000