深度学习入门——Mini-batch、Momentum与Adam算法
基于不同优化算法更新神经网络中的参数
学习记录自:deeplearning.ai-andrewNG-master
一、 优化算法概述
1.1 常用优化算法
在机器学习或深度学习中,一般采取梯度下降对参数进行优化更新,本文主要讨论Mini-Batch算法、Momentum算法、RMSprop以及Adam算法。
1.2 为什么要改进梯度下降
对于一个数据量适中的数据集而言,可以直接利用梯度下降或者随机梯度下降(Stochastic Gradient Descent)。此时在整个训练集进行梯度下降优化不会消耗太多的时间,效率也不会受太大影响。
但是在深度学习中,往往有巨大的数据样本,如果这种情况下,依然对整个样本数据集进行梯度下降,那么整个训练速度很非常慢。以上算法针对此问题进行了探索,提出更合理的梯度下降优化方法。
二、 优化算法原理与实现
2.1 Mini-Batch梯度下降
对非常庞大的数据样本进行整个数据集梯度下降往往耗时耗力,Mini-Batch梯度下降算法很好的解决了这个问题。主要思路在于对庞大的数据集进行样本划分,把原本特别大的数据样本随机划分为一个个的小样本集,其中每个小样本集中含有数量相同的样本个数。再分别对每个小样本集进行训练,实施梯度下降。样本划分的操作涉及Shuffle和Partition。
Shuffle:
如下所示,创建训练集(X,Y)的随机打乱版本。X和Y中的每一列代表一个训练示例。注意,随机打乱是在X和Y之间同步完成的。这样,在随机打乱之后,X的列就是对应于Y中标签的示例。打乱步骤可确保该示例将随机分为不同小批,如图1所示。
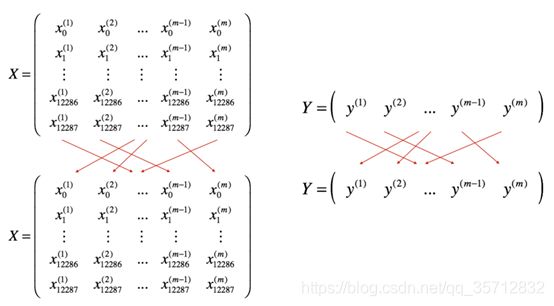
图 1 样本数据集shuffle操作
Partition:
将打乱后的(X,Y)划分为大小为mini_batch_size(此处为64)的小批样本。因为训练示例的数量并不总是可以被mini_batch_size整除,所以取最后剩下的数据样本作为一个小样本集。
下图是利用梯度下降和Mini-batch梯度下降的训练结果。

图 3 梯度下降与Mini-batch梯度下降损失函数对比图
Mini-batch梯度下降法因为样本划分的原因,每个样本集的梯度下降不一定会始终朝着损失函数最小化的方向迭代,所以噪声会更大,但整体趋势也是趋于损失函数最优化。
另外对于Mini-batch算法,如何选择mini-batch-size也是一个问题,根据相关实验与经验,一般的在样本集不超过2000个时,选择一般梯度下降即可。当样本集超过2000个时,经典的mini-batch-size为64、128、256、512等。
2.2 Momentum与RMSprop
从刚刚Mini-batch梯度下降法的损失函数迭代图来看,它的收敛速率并不是特别好,并且优化时存在数值振荡,为了减小优化时的震荡,提出了动量梯度下降法(Momentunm)。
动量梯度下降算法实际上是用了指数加权平均的原理,在讨论Momentum与RMSprop之前,先对指数加权平均进行说明。
指数加权平均
指数加权平均(Exponentially weighted averges),也叫指数加权移动平均,是一种常用的序列数据处理方式,下面给出了某地一年的温度的变化曲线。
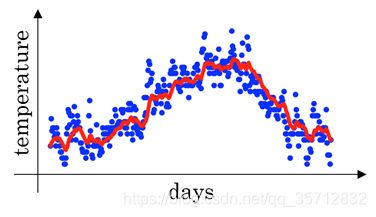
图 4 某地一年的温度变化曲线
其中红色的线条就是利用指数加权平均后拟合得到的温度预测曲线,从图中可以看出,该曲线较好的说明了该地的温度变化情况,以下是指数加权平均的计算公式:

利用指数加权的思想,我们在动量梯度下降中,也采取用这样的方法,把划分好的每个样本集计算得到的梯度拿来平均,以此来表示整个样本集的梯度。在平均的过程中,与优化方向不一致的梯度值会得到中和,达到了减小震荡的目的,如下图所示:
图 5 指数平均达到减小优化时的噪声与震荡
Momentum采用的是常规的指数加权平均,而RMSprop采用的是均方根平均,两种方法都可以消除梯度下降时的摆动,进而达到快速且稳定收敛到最值点附近的目的。
Momentum的实现过程如下:

图 6 Momentum算法实现过程
RMSprop算法的实现与Momentum稍微不同,是对计算到的梯度的平方进行平均,实现过程如下:
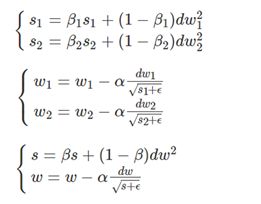
图 7 RMSprop算法实现过程
分母中的 eplison,是为了防止出现除零情况而增加的一个小量,另外alpha 和beta 都是超参数。
三、 算法在模型中的效果
3.1 Momentum算法效果
本文以一个简单的深层神经网络作为模型,对各种算法进行测试。损失函数迭代图和模型分类效果如下图所示:
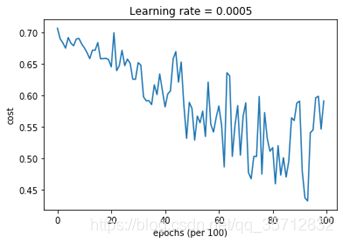
图 9 Momentum算法模型分类效果
3.2 Adam算法效果
Adam算法损失函数迭代图和模型分类效果如下图所示:
图 11 Adam算法模型分类效果
3.3 对比分析
从结果来看Adam明显胜过Mini-batch和Momentum。如果在简单的数据集上运行,那么这三种方法都将产生非常好的结果。但是,Adam收敛得更快。Adam的优势包括:相对较低的内存要求,即使很少调整超参数,通常也能很好地工作。
本文所用到的代码如下:
"""
优化算法的学习
Mini-Batch Momentum Adam
时间: 1/03/2020
"""
#首先导入 需要的包
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
#首先是最常用的 梯度下降
def update_parameters_with_gd(parameters, grads, learning_rate):
L = len(parameters) // 2 # number of layers in the neural networks
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*grads["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] -learning_rate*grads["db" + str(l+1)]
return parameters
#Mini-batch梯度下降
"""
涉及 样本划分 以mini-batch-size 划分 每一个小批次样本 都含有 size个数据 最后一组可能小于size
涉及操作 shuffle -> partition
"""
#从(X,Y)创建随机小批量列表
def random_mini_batches(X, Y, mini_batch_size = 64):
"""
从(X,Y)创建随机小批量列表
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
返回值:
mini_batches -- 小批量后的数据列表 (mini_batch_X, mini_batch_Y)
"""
m = X.shape[1] # 样本数据个数
mini_batches = []
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # 每一块数据的最小批量大小(取下整数)
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# 处理最后一块数据个数小于mini_batch_size的情况 (last mini-batch < mini_batch_size)
if m % mini_batch_size != 0:
#最后剩余的数据 分为一块
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
#Momentum梯度下降 (动量梯度下降法)
"""
利用了指数加权平均 的思想
利用dw 的平均来描述 vdw 在利用vdw 来进行参数更新
冲量beta越大,更新越平滑,因为我们对过去的梯度的考虑也更多。但是,如果太大,也可能使更新变得过于平滑。
beta的常用值范围是0.8到0.999。如果你不想调整它,则0.9通常是一个合理的默认值。
"""
#首先初始化 V[dw1,db1,dw2,db2,....] 注意 这里是 速度 不是梯度
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
返回值:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2 # 神经网络层数
v = {}
# 初始化 V
for l in range(L):
v["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
return v
#利用Momentum 进行梯度下降 参数更新
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
利用 momentum 进行参数更新
"""
L = len(parameters) // 2 # 神经网络层数
# 对每一个参数进行更新 (Mometnum梯度下降)
for l in range(L):
# 计算速度 vdw vdb (vdw = beta*vdw + (1-beta)*dw )
v["dW" + str(l + 1)] = beta*v["dW" + str(l + 1)]+(1-beta)*grads['dW' + str(l+1)]
v["db" + str(l + 1)] = beta*v["db" + str(l + 1)]+(1-beta)*grads['db' + str(l+1)]
# 利用vdw vdb 进行参数更新
parameters["W" + str(l + 1)] = parameters['W' + str(l+1)] - learning_rate*v["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters['b' + str(l+1)] - learning_rate*v["db" + str(l + 1)]
return parameters, v
Adam算法代码:
#Adam 优化算法
"""
Adam算法 会很复杂 它结合了 Mometnum梯度下降 和 RMSprop梯度下降
需要用指数加权平均 计算 vdw vdb 需要用梯度的平方指数加权平均 计算 sdw sdb
需要修正 vdw vdb sdw sdb -> ( vdw vdb sdw sdb )_corrected
需要利用 ( vdw vdb sdw sdb )_corrected 来更新参数 W b
需要利用 epsilon 来避免零除
"""
##初始化参数 V[dw1,db1,...] S[dw1,dw2,...]
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # 神经网络层数
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
v["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l+1)].shape)
v["db" + str(l + 1)] = np.zeros(parameters["b" + str(l+1)].shape)
s["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l+1)].shape)
s["db" + str(l + 1)] = np.zeros(parameters["b" + str(l+1)].shape)
return v, s
##利用 Vdw.. Sdw.. beta1(for V) beta2(for S) epsilon 进行参数更新
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.08,
beta1 = 0.9, beta2 = 0.9, epsilon = 1e-8):
"""
Adam梯度下降 进行参数更新
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # 神经网络层数
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for l in range(L):
#计算 mometnum中的 V (指数加权平均)
v["dW" + str(l + 1)] = beta1*v["dW" + str(l + 1)] +(1-beta1)*grads['dW' + str(l+1)]
v["db" + str(l + 1)] = beta1*v["db" + str(l + 1)] +(1-beta1)*grads['db' + str(l+1)]
#对V 进行修正
v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)]/(1-(beta1)**t)
v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)]/(1-(beta1)**t)
# 计算 RMSprop中的 S (平方指数加权平均)
s["dW" + str(l + 1)] =beta2*s["dW" + str(l + 1)] + (1-beta2)*(grads['dW' + str(l+1)]**2)
s["db" + str(l + 1)] = beta2*s["db" + str(l + 1)] + (1-beta2)*(grads['db' + str(l+1)]**2)
#对S 进行修正
s_corrected["dW" + str(l + 1)] =s["dW" + str(l + 1)]/(1-(beta2)**t)
s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)]/(1-(beta2)**t)
#利用 修正后的 S V 和学习率 epsilon 进行参数更新
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)]-learning_rate*(v_corrected["dW" + str(l + 1)]/np.sqrt( s_corrected["dW" + str(l + 1)]+epsilon))
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)]-learning_rate*(v_corrected["db" + str(l + 1)]/np.sqrt( s_corrected["db" + str(l + 1)]+epsilon))
return parameters, v, s
模型整合
#整合了各种 优化算法的 模型
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0005, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.9, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
# 先初始化神经网络 参数
parameters = initialize_parameters(layers_dims)
# 初始化优化算法
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# 优化迭代 (外层为迭代次数)
for i in range(num_epochs):
#先进行 数据批次划分 Mini_batch 的过程
minibatches = random_mini_batches(X, Y, mini_batch_size)
#对每一块数据 minibatch 进行 遍历
for minibatch in minibatches:
# 数据提取
(minibatch_X, minibatch_Y) = minibatch
# 正向传播
a3, caches = forward_propagation(minibatch_X, parameters)
# 损失计算
cost = compute_cost(a3, minibatch_Y)
# 反向传播
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# 参数更新
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
# 损失函数输出
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# 损失函数可视化
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters
好了 ,这次的优化算法分享就到这儿了!!