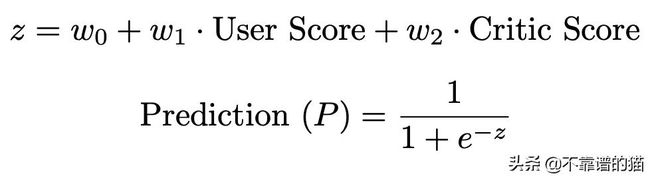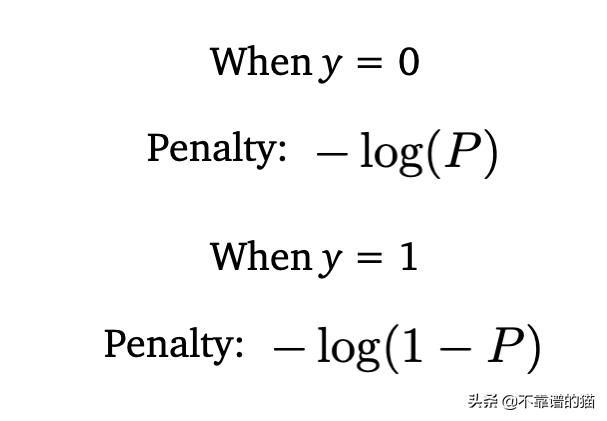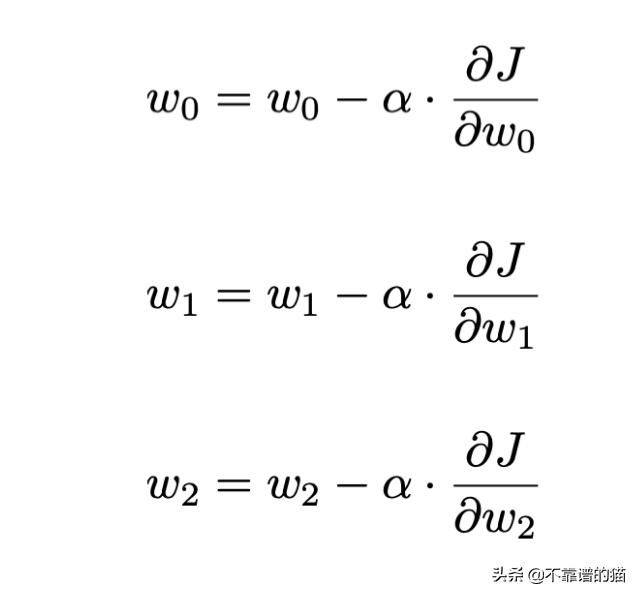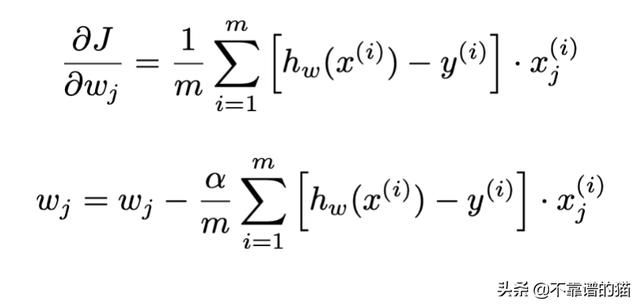分类任务如何用逻辑回归实现_如何使用逻辑回归从头开始创建分类器
在本文中,我将简要描述如何使用逻辑回归从零开始创建分类器。在实践中,您可能会使用诸如scikit-learn或tensorflow之类的包来完成这项工作,但是理解基本的方程和算法对于机器学习非常有帮助。
本文中的所有代码使用Python,所以让我们导入所有需要Python库:
# Import packages%matplotlib inlineimport matplotlib as mplimport matplotlib.pyplot as pltimport numpy as np# General plot parametersmpl.rcParams['font.size'] = 18mpl.rcParams['axes.linewidth'] = 2mpl.rcParams['axes.spines.top'] = Falsempl.rcParams['axes.spines.right'] = Falsempl.rcParams['axes.labelpad'] = 10mpl.rcParams['xtick.major.size'] = 10mpl.rcParams['xtick.major.width'] = 2mpl.rcParams['ytick.major.size'] = 10mpl.rcParams['ytick.major.width'] = 2离散预测
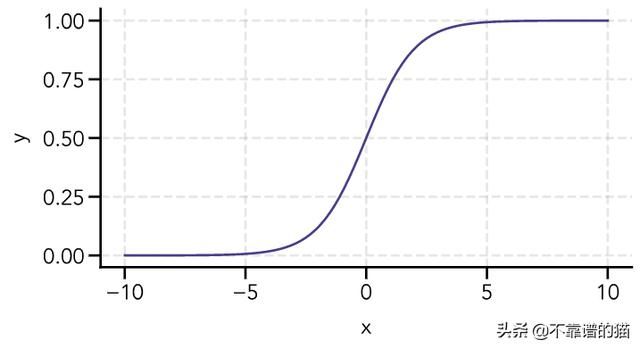
要理解预测算法,最好先选择一个数学函数,它的二进制输出是0或1。我们可以使用logistic或sigmoid函数,它的形式是:
我们可以用Python编写此函数并将其绘制如下:
def sigmoid(z): """Returns value of the sigmoid function.""" return 1/(1 + np.exp(-z))# Calculate sigmoidx = np.linspace(-10, 10, 100)y = sigmoid(x)# Create figurefig = plt.figure(figsize=(8, 4))ax = fig.add_subplot(111)# Plot sigmoidax.plot(x, y, linewidth=2, color='#483d8b')# Add gridax.grid(linestyle='--', linewidth=2, color='gray', alpha=0.2)# Edit y-ticksax.set_yticks([0, 0.25, 0.5, 0.75, 1.0])# Edit axis labelsax.set(xlabel='x', ylabel='y')plt.show()在x = 0附近,sigmoid函数的输出值迅速从0附近变为接近1。由于输出值在y = 0.5附近是对称的,我们可以将其作为决策阈值,其中y≥0.5输出1,y < 0.5输出0。
生成机器学习数据集
我们的场景如下所示:我们正在构建一个简单的电影推荐系统,该系统考虑到0到5之间的user score(所有用户)和0到5之间的critic score。然后,我们的模型应该根据输入数据生成一个决策边界,以预测当前用户是否会喜欢这部电影,并向他们推荐这部电影。
我们将为100部电影设置一组随机的user scores和critic scores:
# For reproducibility - will seed psuedorandom numbers at same pointnp.random.seed(74837)# Random user and critic scoresuser_score = 5*np.random.random(size=100)critic_score = 5*np.random.random(size=100)现在,让我们生成分类:在这种情况下,用户可能喜欢这部电影(1),也可能不喜欢(0)。为此,我们将使用以下决策边界函数。我们将此方程的右侧设置为0,因为它定义了logistic函数等于0.5的情况:
y = np.zeros(len(user_score))boundary = lambda x1, x2: 6 - x1 - 2*x2# Set y = 1 above decision boundaryfor i in range(len(y)): if boundary(user_score[i], critic_score[i]) <= 0: y[i] = 1 else: y[i] = 0注意,在实际数据集中,您不知道决策边界的函数形式是什么。在本教程中,我们定义了一个函数并添加了一些噪声。
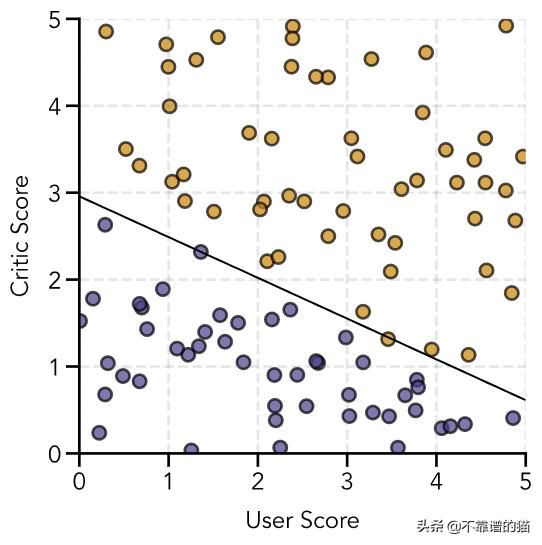
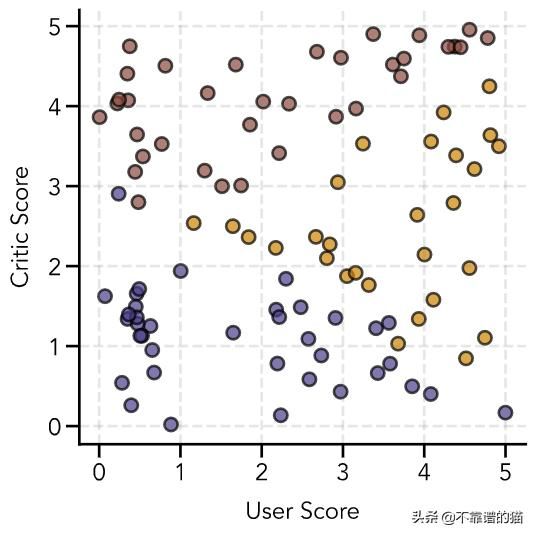
现在,我们可以绘制我们的初始数据,其中一个橙色圆圈表示用户喜欢的电影,一个蓝色圆圈表示用户不喜欢的电影:
# Create figurefig = plt.figure(figsize=(6, 6))ax = fig.add_subplot(111)# Colors for scatter pointscolors = ['#483d8b', '#cc8400']colors_data = [colors[int(i)] for i in y]# Plot sample dataax.scatter(user_score, critic_score, color=colors_data, s=100, edgecolor='black', linewidth=2, alpha=0.7)# Add gridax.grid(linestyle='--', linewidth=2, color='gray', alpha=0.2)# Add axis labelsax.set(xlabel='User Score', ylabel='Critic Score')plt.show()决策边界
为了确定我们的决策边界有多好,我们需要为错误预测定义一个惩罚,我们将通过创建一个成本函数来实现。我们的预测如下:
当P ≥0.5,我们输出1,当P <0.5,我们将输出0,其中W 0,W 1,W 2是需要优化的权重。
为了惩罚错误的分类,我们可以利用对数函数,因为log(1)= 0并且log(0)→-∞。我们可以使用它来创建两个惩罚(penalty)函数,如下所示:
我们可以将其可视化以更清楚地看到这些惩罚函数的效果:
利用输出(y)不是0就是1的事实,我们可以将这两个惩罚(penalty)函数结合在一个表达式中,这个表达式包含了这两种情况:
现在,当我们的输出是1,我们预测的结果接近于0(第一项)时,我们会遭受高惩罚。类似地,当我们的输出为0,我们预测的结果接近于1(第二项)时,也会发生相同的情况。
现在,我们可以采用惩罚函数并将其推广到m个训练实例中,第i个训练实例的标签由(i)表示。我们还将总成本除以m,以获得均值惩罚(就像线性回归中的均方误差一样)。该最终表达式也称为成本函数。我们将我们的两个特征(user score和critic score)称为x₁和x₂。
成本函数
为了找到最佳决策边界,我们必须最小化成本函数,这可以通过梯度下降算法来完成,该算法的本质是:(1)通过计算成本函数的梯度来找到最大减少的方向,(2)通过沿着这个梯度移动来更新权重值。为了更新权重,我们还提供了学习率(α),它确定了我们沿着该梯度移动了多少。选择学习率时需要权衡注意:学习率太小,我们的算法需要太长时间才能收敛;学习率太大,我们的算法实际上可能不会收敛到全局最优值。
最后一个难题是计算上面表达式中的偏导数。我们可以用微积分的链式法则把它分解为:
现在,我们可以把它们放在一起,得到以下梯度表达式和梯度下降更新规则:
初始化变量
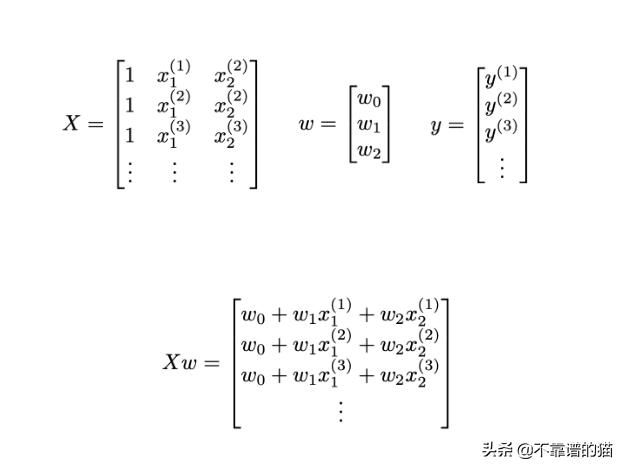
首先,我们将变量初始化如下:
我们现在可以重写前面的函数下,其中上标T表示矩阵的转置:
我们的变量可以初始化如下(我们将所有权重设置为0):
X = np.concatenate((np.ones(shape=(len(user_score), 1)), user_score.reshape(len(user_score), 1), critic_score.reshape(len(critic_score), 1)), axis=1)y = y.reshape(len(y), 1)w = np.zeros(shape=(3, 1))训练模型
以下函数计算成本和梯度值:
def cost_function(X, y, w): """ Returns cost function and gradient Parameters X: m x (n+1) matrix of features y: m x 1 vector of labels w: (n+1) x 1 vector of weights Returns cost: value of cost function grad: (n+1) x 1 vector of weight gradients """ m = len(y) h = sigmoid(np.dot(X, w)) cost = (1/m)*(-np.dot(y.T, np.log(h)) - np.dot((1 - y).T, np.log(1 - h))) grad = (1/m)*np.dot(X.T, h - y) return cost, grad在定义梯度下降函数时,我们必须添加一个称为num_iter的额外输入,它告诉算法在返回最终优化权重之前要进行的迭代次数。
def gradient_descent(X, y, w, alpha, num_iters): """ Uses gradient descent to minimize cost function. Parameters X: m x (n+1) matrix of features y: m x 1 vector of labels w: (n+1) x 1 vector of weights alpha (float): learning rate num_iters (int): number of iterations Returns J: 1 x num_iters vector of costs w_new: (n+1) x 1 vector of optimized weights w_hist: (n+1) x num_iters matrix of weights """ w_new = np.copy(w) w_hist = np.copy(w) m = len(y) J = np.zeros(num_iters) for i in range(num_iters): cost, grad = cost_function(X, y, w_new) w_new = w_new - alpha*grad w_hist = np.concatenate((w_hist, w_new), axis=1) J[i] = cost return J, w_new, w_hist现在,使用以下Python代码训练我们的机器学习模型!
J, w_train, w_hist = gradient_descent(X, y, w, 0.5, 2000)在实际情况中,为了交叉验证和测试模型,我们需要拆分训练数据,但是本教程主要用于演示,我们将使用所有的训练数据。
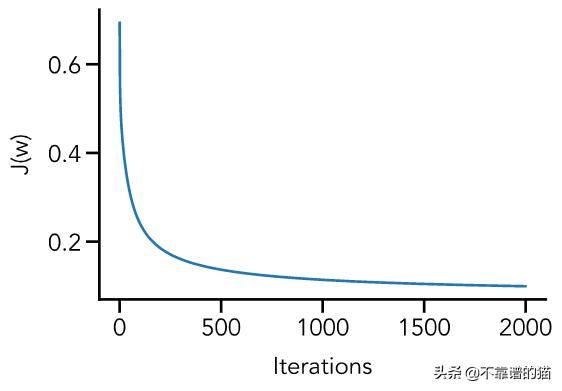
为了确保实际上每次迭代都在降低成本函数的值,可视化图像的Python代码如下:
# Create figurefig = plt.figure(figsize=(6, 4))ax = fig.add_subplot(111)# Plot costsax.plot(range(len(J)), J, linewidth=2)# Add axis labelsax.set(xlabel='Iterations', ylabel='J(w)')plt.show()现在是关键时刻,我们可以绘制决策边界。我们将其覆盖到原始图上的方法是定义一个点网格,然后使用经过训练的权重计算sigmoid函数的预测值。
# Create figurefig = plt.figure(figsize=(6, 6))ax = fig.add_subplot(111)# Colors for scatter pointscolors = ['#483d8b', '#cc8400']colors_data = [colors[int(i)] for i in y]# Plot decision boundaryx1_bound, x2_bound = np.meshgrid(np.linspace(0, 5, 50), np.linspace(0, 5, 50))prob = sigmoid(w_train[0] + x1_bound*w_train[1] + x2_bound*w_train[2])ax.contour(x1_bound, x2_bound, prob, levels=[0.5], colors='black')# Plot sample dataax.scatter(user_score, critic_score, color=colors_data, s=100, edgecolor='black', linewidth=2, alpha=0.7)# Add gridax.grid(linestyle='--', linewidth=2, color='gray', alpha=0.2)# Add axis labelsax.set(xlabel='User Score', ylabel='Critic Score')plt.show()我们现在可以编写一个函数,根据这个训练好的模型做出预测:
def predict(X, w): """ Predicts classifiers based on weights Parameters X: m x n matrix of features w: n x 1 vector of weights Returns predictions: m x 1 vector of predictions """ predictions = sigmoid(np.dot(X, w)) for i, val in enumerate(predictions): if val >= 0.5: predictions[i] = 1 else: predictions[i] = 0 return predictions现在,让我们对新实例进行预测:
X_new = np.asarray([[1, 3.4, 4.1], [1, 2.5, 1.7], [1, 4.8, 2.3]])print(predict(X_new, w_train))#[[1.] [0.] [1.]]多类分类
现在我们已经完成了制作二元分类器的所有工作,将其扩展到多类上是相当简单的。我们将使用一个名为one-vs-all的分类策略,其中我们为每个不同的类训练一个二元分类器,并选择sigmoid函数返回的最大值对应的类。
让我们构建模型:这次用户可以给电影评分0星,1星或2星。
首先,我们再次生成数据并应用两个决策边界:
np.random.seed(7839374)# Random user and critic scoresuser_score = 5*np.random.random(size=100)critic_score = 5*np.random.random(size=100)y = np.zeros(len(user_score))boundary_1 = lambda x1, x2: 6 - x1 - 2*x2boundary_2 = lambda x1, x2: 4 + x1 - 2*x2for i in range(len(y)): if (boundary_1(user_score[i], critic_score[i]) + 0.5*np.random.normal() <= 0): if (boundary_2(user_score[i], critic_score[i]) <= 0): y[i] = 2 else: y[i] = 1 else: y[i] = 0# Create figurefig = plt.figure(figsize=(6, 6))ax = fig.add_subplot(111)# Colors for scatter pointscolors = ['#483d8b', '#cc8400', '#8b483d']colors_data = [colors[int(i)] for i in y]# Plot sample dataax.scatter(user_score, critic_score, color=colors_data, s=100, edgecolor='black', linewidth=2, alpha=0.7)# Add gridax.grid(linestyle='--', linewidth=2, color='gray', alpha=0.2)# Add axis labelsax.set(xlabel='User Score', ylabel='Critic Score')plt.show()我们的数据集如下所示,其中蓝色圆圈代表0星,橙色圆圈代表1星,红色圆圈代表2星:
对于我们训练的每个二进制分类器,我们将需要重新标记数据,以便将我们感兴趣的类的输出设置为1,并将所有其他标签设置为0。例如,如果我们有3组A(0) ,B(1)和C(2)—我们必须制作三个二进制分类器:
对于我们训练的每个二元分类器,我们需要重新标记数据,以便我们感兴趣的类的输出被设置为1,其他标签被设置为0。我们必须创建3个二元分类器:
(1)A设为1,B和C设为0
(2)B设为1,A和C设为0
(3)C设为1,A和B设为0
下面的函数为每个分类器重新标记我们的数据:
def relabel_data(y, label): """ Relabels data for one-vs-all classifier Parameters y: m x 1 vector of labels label: which label to set to 1 (sets others to 0) Returns relabeled_data: m x 1 vector of relabeled data """ relabeled_data = np.zeros(len(y)) for i, val in enumerate(y): if val == label: relabeled_data[i] = 1 return relabeled_data.reshape(len(y), 1)现在,我们进行模型训练:
# Initialize variablesX = np.concatenate((np.ones(shape=(len(user_score), 1)), user_score.reshape(len(user_score), 1), critic_score.reshape(len(critic_score), 1)), axis=1)y = y.reshape(len(y), 1)w = np.zeros(shape=(3, 1))y_class1 = relabel_data(y, 0)_, w_class1, _ = gradient_descent(X, y_class1, w, 0.5, 2000)y_class2 = relabel_data(y, 1)_, w_class2, _ = gradient_descent(X, y_class2, w, 0.5, 2000)y_class3 = relabel_data(y, 2)_, w_class3, _ = gradient_descent(X, y_class3, w, 0.5, 2000)绘制决策边界这一次稍微复杂一些。我们必须为每个经过训练的分类器计算网格中每个点的预测值。然后我们选择每个点的最大预测值,并根据导致该最大值的分类器为其分配相应的类。我们选择绘制的轮廓线为0.5(在0和1之间)和1.5(在1和2之间):
# Create figurefig = plt.figure(figsize=(6, 6))ax = fig.add_subplot(111)# Colors for scatter pointscolors = ['#cc8400', '#483d8b', '#8b483d']colors_data = [colors[int(i)] for i in y]# Plot decision boundariesx1_bound, x2_bound = np.meshgrid(np.linspace(-0.05, 5.05, 500), np.linspace(-0.05, 5.05, 500))prob_0 = sigmoid(w_class1[0] + x1_bound*w_class1[1] + x2_bound*w_class1[2])prob_1 = sigmoid(w_class2[0] + x1_bound*w_class2[1] + x2_bound*w_class2[2])prob_2 = sigmoid(w_class3[0] + x1_bound*w_class3[1] + x2_bound*w_class3[2])prob_max = np.zeros(shape=x1_bound.shape)for i in range(prob_max.shape[0]): for j in range(prob_max.shape[1]): maximum = max(prob_0[i][j], prob_1[i][j], prob_2[i][j]) if maximum == prob_0[i][j]: prob_max[i][j] = 0 elif maximum == prob_1[i][j]: prob_max[i][j] = 1 else: prob_max[i][j] = 2ax.contour(x1_bound, x2_bound, prob_max, levels=[0.5, 1.5], colors='black', linewidths=2)# Plot sample dataax.scatter(user_score, critic_score, color=colors_data, s=100, edgecolor='black', linewidth=2, alpha=0.7)# Add gridax.grid(linestyle='--', linewidth=2, color='gray', alpha=0.2)# Add axis labelsax.set(xlim=(-0.05, 5.05), ylim=(-0.05, 5.05), xlabel='User Score', ylabel='Critic Score')plt.show()这是我们训练过的决策边界!
最后,我们做一个预测函数。为此,我们将使用一个小技巧——我们将对每个实例中的每个分类器进行预测;接下来,我们将把每组预测作为一个新列附加到预测矩阵中;接下来通过遍历每一行并选择具有最大值的列索引,然后获得分类器标签!
def predict_multi(X, w): """ Predicts classifiers based on weights Parameters X: m x n matrix of features w: array of n x 1 vectors of weights Returns predictions: m x 1 vector of predictions """ predictions = np.empty((X.shape[0], 0)) # Gather predictions for each classifier for i in range(len(w)): predictions = np.append(predictions, sigmoid(np.dot(X, w[i])), axis=1) return np.argmax(predictions, axis=1).reshape(X.shape[0], 1)X_new = np.array([[1, 1, 1], [1, 1, 4.2], [1, 4.5, 2.5]])print(predict_multi(X_new, [w_class1, w_class2, w_class3]))# [[0] [2] [1]]