深度学习中的数值微分

梯度决定信息前进的方向，不得不提到一个导数的概念，在某一个瞬间的变化量。

一个小例子

定义一个函数，运用数值微分进行简单求导

$$y=0.01\ast x^2+0.1\ast x$$

def numerical_diff(f,x):
    h = 1e-4
    return (f(x+h)-f(x-h)) / (2*h)

def func(x):
    return 0.01*x**2 + 0.1*x

画图看看这个函数图像

import numpy as np
import matplotlib.pyplot as plt
import warnings 
warnings.filterwarnings('ignore')

x = np.arange(0.0,20.0,0.1)
y = func(x)
plt.xlabel('X')
plt.ylabel('Y')
plt.plot(x,y)

[]

计算x=5和x=10的导数

numerical_diff(func,5)

0.1999999999990898

numerical_diff(func,10)

0.2999999999986347

谈谈偏导数

有这么一个函数

$$f(x_0,x_1)=x_0^2+x_1^2$$

def func_1(x):
    return x[0]**2 + x[1]**2

x[1:]

array([ 0.1,  0.2,  0.3,  0.4,  0.5,  0.6,  0.7,  0.8,  0.9,  1. ,  1.1,
        1.2,  1.3,  1.4,  1.5,  1.6,  1.7,  1.8,  1.9,  2. ,  2.1,  2.2,
        2.3,  2.4,  2.5,  2.6,  2.7,  2.8,  2.9,  3. ,  3.1,  3.2,  3.3,
        3.4,  3.5,  3.6,  3.7,  3.8,  3.9,  4. ,  4.1,  4.2,  4.3,  4.4,
        4.5,  4.6,  4.7,  4.8,  4.9,  5. ,  5.1,  5.2,  5.3,  5.4,  5.5,
        5.6,  5.7,  5.8,  5.9,  6. ,  6.1,  6.2,  6.3,  6.4,  6.5,  6.6,
        6.7,  6.8,  6.9,  7. ,  7.1,  7.2,  7.3,  7.4,  7.5,  7.6,  7.7,
        7.8,  7.9,  8. ,  8.1,  8.2,  8.3,  8.4,  8.5,  8.6,  8.7,  8.8,
        8.9,  9. ,  9.1,  9.2,  9.3,  9.4,  9.5,  9.6,  9.7,  9.8,  9.9,
       10. , 10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 11. ,
       11.1, 11.2, 11.3, 11.4, 11.5, 11.6, 11.7, 11.8, 11.9, 12. , 12.1,
       12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 13. , 13.1, 13.2,
       13.3, 13.4, 13.5, 13.6, 13.7, 13.8, 13.9, 14. , 14.1, 14.2, 14.3,
       14.4, 14.5, 14.6, 14.7, 14.8, 14.9, 15. , 15.1, 15.2, 15.3, 15.4,
       15.5, 15.6, 15.7, 15.8, 15.9, 16. , 16.1, 16.2, 16.3, 16.4, 16.5,
       16.6, 16.7, 16.8, 16.9, 17. , 17.1, 17.2, 17.3, 17.4, 17.5, 17.6,
       17.7, 17.8, 17.9, 18. , 18.1, 18.2, 18.3, 18.4, 18.5, 18.6, 18.7,
       18.8, 18.9, 19. , 19.1, 19.2, 19.3, 19.4, 19.5, 19.6, 19.7, 19.8,
       19.9])

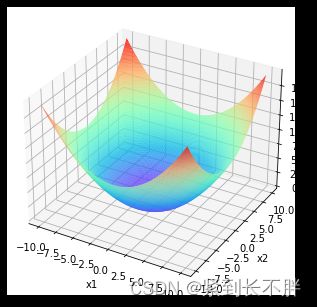
它大致的三维图像如此

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


fig = plt.figure()
ax = Axes3D(fig)
x = np.arange(-10.0,10.0,0.1).reshape(-1,2)
x1 = x[0:]
x2 = x[1:]
X1, X2 = np.meshgrid(x1,x2)
Z = X1**2 + X2**2
plt.xlabel('x1')
plt.ylabel('x2')
ax.plot_surface(X1, X2, Z, rstride=1, cstride=1, cmap='rainbow')
plt.show()

问题1：求$x_0=3,x_1=4$时，关于$x_0$的偏导数

def func_x0(x0):
    return x0*x0 + 4.0**2.0

numerical_diff(func_x0,3.0)

6.00000000000378

问题1：求$x_0=3,x_1=4$时，关于$x_1$的偏导数

def func_x1(x1):
    return 3.0**2 + x1*x1

numerical_diff(func_x1,4.0)

7.999999999999119

梯度

梯度是什么呢？从上面计算可以初略的总结：
由全部变量汇总成的向量叫梯度

即:

[6.00000000000378,7.999999999999119]

def numerical_gradient(f,x):
    h = 1e-4 
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        # f(x+h)的计算
        x[idx] = tmp_val + h
        fxh1 = f(x)
        
        # f(x-h)的计算
        x[idx] = tmp_val - h
        fxh2 = f(x)
        
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val 
    return grad

问题来了：求点(3，4)、(0，2)、(3，0)的梯度

numerical_gradient(func_1,np.array([3.0,4.0]))

array([6., 8.])

numerical_gradient(func_1,np.array([0.0,2.0]))

array([0., 4.])

numerical_gradient(func_1,np.array([3.0,0.0]))

array([6., 0.])

梯度法

求完梯度，以此为信息，并决定下一次的前进方法，从而实现组建减小函数值的过程就是梯度法

$$x_0=x_0-learningrate\ast 梯度$$

下面基于python实现梯度下降法

def gradient_descent(f,init_x,lr=0.01,step_num = 100):
    x = init_x
    
    for i in range(step_num):
        grad = numerical_gradient(f,x)
        x -= lr * grad
        
    return x
    

试一试求$$f(x_0+x_1)=x_0^2+x_1^2$$的最小值

init_x = np.array([-3.0,4.0])
gradient_descent(func_1,init_x=init_x,lr = 0.1,step_num=100)

array([-6.11110793e-10,  8.14814391e-10])

有时候学习率的不同，可能会影响我们的结果

当学习率过大时

gradient_descent(func_1,init_x=init_x,lr = 10,step_num=100)

array([ 2.34235971e+12, -3.96091057e+12])

当学习率过小时

gradient_descent(func_1,init_x=init_x,lr = 0.001,step_num=100)

array([ 2.34235971e+12, -3.96091057e+12])

一般而言，学习率需要通过人工设定，设定的同时需要工作者不断的尝试，以此来获得一个可靠的结果