回归分析——从一元线性回归到Lasso回归

一、一元线性回归

一元线性回归模型就是一个自变量和一个因变量，二者之间具有线性关系，通过计算参数，拟合数据。

回归方程：$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

参数${\theta }_0$为截距，参数${\theta }_1$为斜率，为求解这两个参数以拟合数据，需要制定一个拟合标准，也就是什么情况下叫做拟合得很好，什么情况下叫做拟合效果很差？这就引入了代价函数（也称损失函数），使得代价函数最小的拟合被认为是拟合效果最好的线性回归。

设真实值为$y$，预测值为$h_{\theta }(x)$，则真实值与预测值之间的误差平方和为$(y-h_{\theta }(x){)}^2$

（使用平方和是为了避免正负误差之间相互抵消）

代价函数：$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(y^i-h_{\theta }(x^i){)}^2$

（这里求得了所有x对应的误差平方和求和，除以$2m$是为了方便后面求导，不影响代价函数的相对大小）

求使得代价函数最小的参数（一元线性回归中是${\theta }_0,{\theta }_1$）就是线性回归的过程，求解方法主要有两种，梯度下降法和正规方程法。

先来看梯度下降法

1、梯度下降法

核心思想：要找到某函数的最值（最大值或最小值），最好的方法是沿着该函数的梯度去探寻。（梯度：一个函数的全部偏导数构成的向量，梯度向量的方向为函数值变化最快的方向）

求解步骤：

初始化参数（${\theta }_0,{\theta }_1$）

不断改变${\theta }_0,{\theta }_1$，直到$J({\theta }_0,{\theta }_1)$达到一个全局最小值（也可能陷入局部最小值）

如何改变？根据梯度下降的核心思想，改变的方式主要是往梯度的方向趋近，因为这个方向变化最快，更容易找到极值，一定迭代次数后代价函数数值落到极小值附近，对应的参数就是拟合需要的最佳参数。

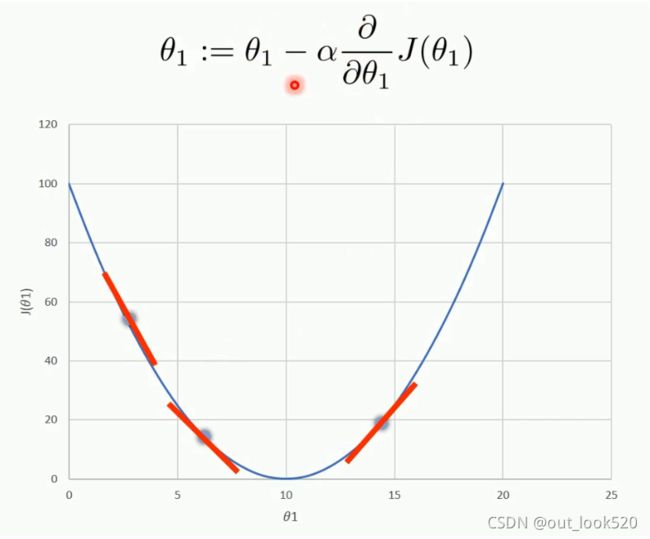
迭代式：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)forj=0andj=1$

其中，$\alpha$为学习率，决定了梯度变化的速度（也就是变化步长），$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$为代价函数的梯度，决定梯度变化方向。

更新方式：同步更新${\theta }_0和{\theta }_1$

$tem{p}_0:={\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)$

$tem{p}_1:={\theta }_1-\alpha \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)$

${\theta }_0:=tem{p}_0$

${\theta }_1:=tem{p}_1$

学习率的选择对于梯度下降法很重要，学习率太小会导致拟合速度过慢；学习率太大，会容易错过极值，在极值附近不断震荡。

对于迭代式的理解可以拿其中一个参数，进行理解，图中给出了参数${\theta }_1$也就是斜率的迭代过程，初始参数值为程序随机设置（或人为设置）的一个值，通过梯度求解（只有一个参数的话也就是求导数了）确定梯度方向，最左边的点的梯度即为一个较大的负值，方向为斜率的方向，进行迭代，${\theta }_1$减去一个较大的负值，也就是加上一个较大的正值，参数${\theta }_1$变大，斜率变大，迭代一次后也就重新确立了一个方程$J({\theta }_1)$，重复上述过程，直到达到一定的迭代次数，使得代价函数最小。从这幅图总结迭代的方式就是参数向着导数的方向不断变化，向导数为0的位置趋近，负了就增大，正了就减小。推广到梯度上也是如此，整体上朝着梯度的方向变化就可以找到最小值（局部或全局）。

梯度求解：

$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(y^i-h_{\theta }(x^i){)}^2$

$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$

当$j=0:\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}{)}_{}-y^{(i)})$

当$j=1:\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^i$

迭代更新${\theta }_0和{\theta }_1$寻找最小值：

${\theta }_0:={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$

${\theta }_1:={\theta }_1-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^{(i)}$

需要注意的点：线性回归的代价函数是凸函数，所以无论初始值怎么选取，都可以走到全局最小值处，不存在局部最优解的情况；而非凸函数有很多的局部最小值，使用梯度下降法可能陷入局部最小值处，不能得到很好的结果，初始值的选取就对这类函数的最优值求解有很大的影响了。

非凸函数：

2、正规方程法

该方法顾名思义也就是利用方程去求解参数，设$\omega$表示参数列向量（待求解的），$X$表示样本列向量（已知数据集），$Y$为因变量列向量（真实值），回归方程就是$h_{\theta }(X)={\omega }^{T}X$。

对于一元回归方程，$\omega =[{\omega }_0,{\omega }_1]，X=[X_0,X_1]$，其中${\omega }_0$为截距，${\omega }_1$为斜率，$X_0$为1，$X_1$为一个自变量，$h_{\theta }(X)={\omega }_0{X}_0+{\omega }_1{X}_1$。

平方误差：${\sum }_{i=1}^m(y_i-x_i^T\omega {)}^2$，（$y_i,x_i$为某一行数据的具体数据，也就是一条样本数据，$y_i$为对应真实值，$x_i$为特征值），用矩阵表示可以写成$(Y-X\omega {)}^T(Y-X\omega )$

求解使得平方误差最小的回归系数$\omega$，对目标函数进行对$\omega$的求导：

$\frac{\partial (y-X\omega {)}^T(y-X\omega )}{\partial \omega }=\frac{\partial (y^{T}y-y^{T}X\omega -{\omega }^T{X}^{T}y+{\omega }^T{X}^{T}Xw)}{\partial \omega }$

$=0-X^{T}y-X^{T}y+2X^{T}X\omega$

$=-2X^T(y-X\omega )$

令偏导为0，得到

$X^{T}y-X^{T}X\omega =0$

$\hat{\omega }=(X^{T}X{)}^{-1}{X}^{T}y$

$\hat{\omega }$ 即表示当前可以估计处的$\ \omega\ $的最优解，是一个最佳估计

得到的求解公式中包含$(X^{T}X{)}^{-1}$，需要对矩阵求逆，因此该方程只有在逆矩阵存在时适用，矩阵的逆可能不存在（如存在线性相关的特征也就是多重共线性或是特征数据太多使得样本数m<=特征数量n），所以需要调用numpy中的linalg.det() 函数计算行列式判断矩阵是否可逆。对于正规方程法求解系数，只需要在代码中进行矩阵计算即可得到最佳参数用以拟合数据。

3、梯度下降与正规方程的比较

用一个表格进行简单的比较：

梯度下降	正规方程
需要选择学习率$\alpha$	不需要
需要进行多次迭代	一次矩阵运算即可得出
只能得到最优解的近似值	可以得到全局最优解
当特征数量n很大时也能使用	n小于10000时适用，否则计算量太大（需要计算$(X^{T}X{)}^{-1}$，时间复杂度大约是$O(n^3)$）
适用于各种类型的模型	只适用于线性模型

可以看到正规方程的局限性是较大的，但在代码实现上较为简单，在数据量较小的线性拟合中可以使用。

4、代码实现一元线性回归

1）梯度下降

实现思路：迭代epochs次，每次迭代先根据公式

$j=0:\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}))$

$j=1:\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}))x^i$

求解梯度，再根据公式

${\theta }_0:={\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)$

${\theta }_1:={\theta }_1-\alpha \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)$​

更新参数${\theta }_0和{\theta }_1$，后续可根据拟合的效果不断调整学习率$\alpha$和迭代次数 epochs 。

代码实现：

# 学习率learning rate
lr = 0.1
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 3000

# 计算代价函数的值
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k*x_data[i] + b)) **2
    return totalError / float(len(x_data)) / 2

# 梯度下降法求解参数
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        # 初始化梯度
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和平均
        for j in range(len(x_data)):
            b_grad += (1/m)*((k*x_data[j] + b) - y_data[j])
            k_grad += (1/m)*x_data[j]*((k*x_data[j] + b) - y_data[j])
        # 更新参数b和k
        b = b - (lr*b_grad)
        k = k - (lr*k_grad)
    return b, k

2）正规方程

实现思路：先利用numpy.linalg.det()判断矩阵是否可逆，可逆则利用公式

$\hat{\omega }=(X^{T}X{)}^{-1}{X}^{T}y$

求解估计最佳参数

代码实现：

def stand_regression(x_arr, y_arr):
    """
    计算回归系数w
    :param x_arr: x数据集
    :param y_arr: y数据集
    :return:
        ws - 回归系数
    """
    x_mat = np.mat(x_arr)
    y_mat = np.mat(y_arr).T
    # w = (X.T * X)^-1 * X.T * Y
    xTx = x_mat.T * x_mat
    # 调用numpy中的linalg.det()计算行列式来判断是否可对xTx求逆
    if np.linalg.det(xTx) == 0.0:
        print("This matrix is singular, can't do inverse")
        return
    ws = xTx.I * (x_mat.T * y_mat)
    return ws

二、多元线性回归

一般数据中都不会只有一个特征，往往会有多个特征，这时回归方程可以设为：

$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$

向量表示为$h_{\theta }(x)={\theta }^{T}X$

代价函数：$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}{\sum }_{i=1}^m(y^i-h_{\theta }(x^i){)}^2$

迭代式：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1,...,{\theta }_n)$

$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})x_j^{(i)})$

跟一元线性回归也没啥区别，就是多了几维特征

三、多项式回归

有时数据之间呈现的关系可能并不是线性的，用线性回归拟合会欠拟合，对于非线性的拟合核心思想是新增高次项特征，我的理解是通过项的增加将低维特征转至高维，在更高维数据间的关系是线性的。

一次方程：$y=ax+b$

二次方程：$y=a{x}^2+bx+x$

在二次方程中，将$x^2$看作一个特征，这样二次方程就变成了$y=a{x}_1+b{x}_2+c,(x_1=x_2^2)$，可以利用多元线性回归进行参数求解，所以对于多项式回归问题，简单来说就是将多元回归通过高次项的特征构造转换为多元线性回归求解。

使用更高阶的多项式虽然可能比简单的线性回归效果要好，但也更容易过拟合，对于阶数的选择可以利用交叉验证进行选择。

四、岭回归

如果数据的特征比样本点还多（n>m）怎么办？利用正规方程求解的话，由于数据矩阵X不可能是满秩矩阵了（线性代数的知识），非满秩矩阵在求逆时会出现问题；而利用梯度下降法的话，由于特征数比样本点多，得到的模型容易过拟合（复杂模型对应简单数据易过拟合），这时，缩减参数也即减少特征数是一个不错的方法，岭回归、Lasso等回归算法即利用了这样的思想。

岭回归，一开始是为了解决矩阵X不满秩提出的方法，具体就是在矩阵$X^{T}X$上加一个$\lambda I$使得能够对$(X^{T}X+\lambda I)$求逆（矩阵$I$是一个 m×m的单位矩阵，对角线上元素全为1，$\lambda I$为满秩矩阵，加上非满秩矩阵$X^{T}X$得到的是一个满秩矩阵），$\lambda$是岭系数，一般是一个很小的值，只是添加一点扰动使其成为满秩矩阵。现在岭回归也用来在估计中引入一些偏差，平衡方差&偏差，从而得到更好的估计。

岭回归的回归系数计算式：

$\hat{\omega }=(X^{T}X+\lambda I{)}^{-1}{X}^{T}y$

对应梯度下降中的代价函数表达式为：

$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x_i)-y_i{)}^2+\lambda {\sum }_i^m{\theta }_i^2$

$\lambda {\sum }_i^m{\theta }_i^2$为$L_2$正则项

超参数$\lambda$选择标准：

• 误差平方和增大不太多

• 各回归系数的岭估计基本稳定

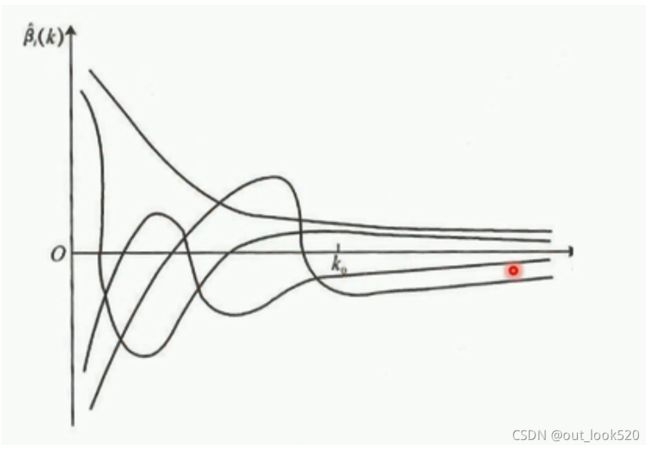
• 越小越好

下图中每条线表示不同的系数估计值随着超参数$\lambda$的变化的变化，随着$\lambda$的增大，各系数估计值逐渐趋于稳定，有些系数估计值甚至趋于了0，但不会等于0，因为加入的正则化只是一个偏差，用于平衡模型，所以整个正则项的值也不能很大。而误差平方和也是模型评价的关键，拟合程度越高，其值也就越小，所以控制误差平方和的值也很关键。

五、Lasso回归

岭回归限定了所有回归系数的平方和不能大于$\lambda$，使用普通的最小二乘法回归在当两个或更多的特征相关时（即存在多重共线性），可能会得出一个很大的正系数和一个很大的负系数，限制条件$\omega$的平方和小于等于$\lambda$的存在使得岭回归避免了这样的问题。另一个缩减方法Lasso回归也是通过对回归系数做了类似的限定：回归系数绝对值的和不大于$\lambda$。在这样的限定条件下，当$\lambda$足够大的时候，一些系数会因此被迫缩减到0，这个特性帮助我们更好的理解数据，但由于绝对值的存在也极大的增加了计算复杂度。

Lasso回归的代价函数：

$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x_i)-y_i{)}^2+\lambda {\sum }_i^m|{\theta }_i|$

$\lambda {\sum }_i^m|{\theta }_i|$为$L_1$正则项

Lasso擅长处理具有多重线性的数据，与岭回归一样是有偏估计

六、岭回归与Lasso回归的区别

岭回归与Lasso回归的出现都是为了解决线性回归出现的过拟合以及通过正规方程求解回归系数时出现的X^TX不可逆的情况，两种回归都对回归系数进行了限定（均是通过在损失函数中引入正则化项来达到目的的）

正则化：为防止过拟合的问题，在损失函数中增加一个每个特征的惩罚因子就是正则化。回归中的$\lambda$称为正则化参数，如果$\lambda$选取过大，会把所有参数$\omega$均最小化，造成欠拟合（误差平方和太大），如果选取过小，会导致过拟合（偏差太小），所以对于超参数$\lambda$的选取很重要。

岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数（平方）惩罚项，Lasso回归引入的是L1范数惩罚项（绝对值）。Lasso回归能够使得损失函数中的许多回归系数均变为0，降低模型的复杂度，而岭回归的所有回归系数都是存在的，只是减小不重要参数的系数。Lasso极大的增大了计算复杂度，但由于系数的减少一定程度上减小了计算量，增加了模型的可解释性。

• 对于岭回归，当$\lambda =0$时，损失函数与线性回归的损失函数一致，没有任何惩罚作用；当 $\lambda$趋近于无穷时，惩罚项也就是无穷大，而为了使代价函数最小，只能压缩系数$\theta$趋近于0（求导趋于0进行求解最值），但是$\lambda$不可能为无穷大，二项式（惩罚项）求偏导时总会保留变量本身，所以事实上也不可能真正地将某个特征压缩为0，尽管系数较小可以有效减小方差，但依然留着一大长串会使模型不便于解释，这是岭回归的缺点。

• 对于Lasso回归，Lasso回归的惩罚项为L1范式，一次项求导可以抹去变量本身，因此Lasso回归的系数可以为0，这样可以起到真正的特征筛选效果

• 无论是岭回归还是Lasso回归，本质都是通过调节$\lambda$来实现模型为误差&方差的平衡调整

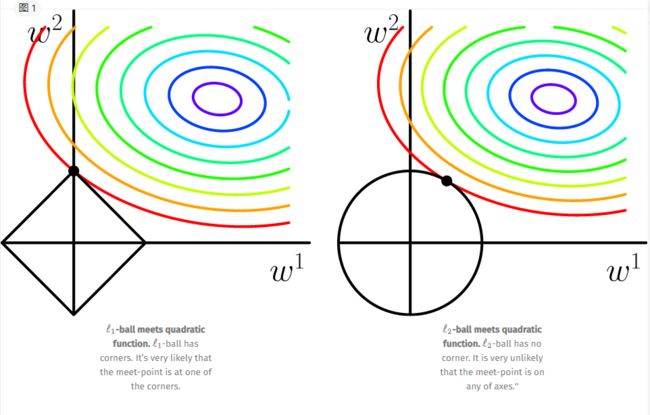
Lasso回归可产生稀疏性，即回归系数解中有多项为0，其产生稀疏性的原因是L1约束使得最优解处会有角的可能性很大，在角的位置会产生稀疏性，而L2约束为圆形域，最优解出现的地方出现在具有稀疏性的位置的概率就变得非常小了。