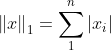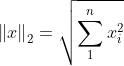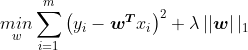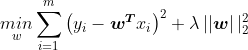一、线性模型----Lasso、Ridge回归及正则化的初步理解
一些基本概念
正则性：
正则性一般用来刻画函数的光滑程度，正则性越高，函数的光滑性越好。通常用Lipschitz指数k来表征函数的正则性。Lipschitz指数刻画了函数f与局部多项式的逼近程度，而函数与局部多项式的逼近程度又与函数的可微性相联系。
向量范数：
距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化的距离概念，它在定义上比距离多了一条数乘的运算法则。有时为了便于理解，我们可以把范数当作距离来理解。
L-P范数：与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下
![L_{p} = \sqrt[p]{\sum_{1}^{n}x_{i}^{p}},x=\left ( x_{1} ,x_{2} ,...,x_{n} \right )](http://img.e-com-net.com/image/info8/61322e60586343bc97e802f852e2a7de.gif)
L0范数：L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。
#代表计数。显然L0范数不连续，难以优化求解。
L1范数：向量中各元素绝对值的和。
L2范数：类似于欧式距离，向量中各元素的平方和再开方。
过拟合与欠拟合：
欠拟合：对样本的一般性质尚未学好，如绿色的就是树叶。
过拟合：把样本自身独有的特性当做了所有潜在样本都会有的共性，必须周围有锯齿才是树叶。
为什么要正则化
正则化是特征选择的一种，目的是为了避免过拟合，而过拟合是非常麻烦的问题。一方面我们希望训练的模型足够强大，使得训练样本上的经验误差小，也就是通常所用到的均方误差小。另一方面，我们又希望模型具有良好的泛化能力，即给定新样本时预测值能够接近其真实值。而过拟合带来的问题就是，在训练样本上的性能极佳，而到了真实的预测阶段效果反而不尽人意。因为训练集样本中的某些特征对于最后的预测并没有起到关键作用，相反可能因为这些特征上的异常取值影响模型性能。而正则化的目的就是使得这些特征的影响变小(L1正则)，甚至直接剔除这些属性的影响(L2正则)。
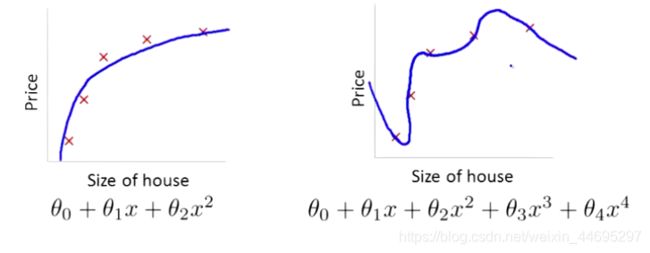
过多的特征，同时只有非常少的训练数据，n_features>>n_samples，会容易导致出现过度拟合的问题。比如上面的右图。这样模型会千方百计的去拟合训练数据，但是，这实际上是一条很扭曲的曲线，它不停上下波动。同时如果我们没有足够的数据集（训练集）去约束这个变量过多的模型，那么就会发生过拟合。这样会导致它无法泛化到新的数据样本中，以至于无法预测新样本值。
正则化就是通过添加惩罚函数，从而使得上图中
这两项的参数
变小，而减小其影响。实际上，这些参数的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，因此 就不易发生过拟合的问题。
L1正则化----Lasso
L2正则化----Ridge
L1+L2----ElasticNet
其中式子的前半部分我们称为经验风险(衡量真实值与预测值之间的误差)，后半部分称为结构风险(欲使模型尽可能简单)。 而系数
称为正则化参数，也是一个超参数。 λ 要做的就是控制在两个不同的目标中的平衡关系。越大，惩罚程度越高，所有的
都将趋近于0，这样最后的拟合曲线就会接近一条直线y=b，变成了欠拟合。ElasticNet的结构风险同时考虑了L1与L2正则，参数
起到了平衡这两项的作用。实际使用中一般使用交叉验证来确定这两个超参数。
L1与L2的比较
为什么不直接用L0呢？一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。所以大家使用的都是L1或L2正则。
1）L1正则更容易产生“稀疏解”。
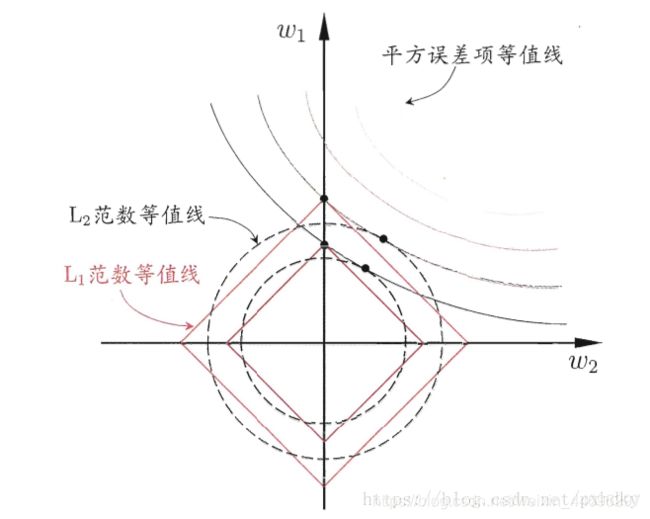
其中的非零分量所对应的特征就是我们认为重要并保留下来的特征，这就有了自动选择特征的能力。假设
仅有两个属性，只有两个参数
，绘制不带正则项的目标函数-平方误差项等值线，再绘制
，
范数等值线，如图正则化后优化目标的解要在平方误差项和正则化项之间折中，即出现在图中等值线相交处采用。范数时，交点常出现在坐标轴上，即
或
为0；而采用范数时，交点常出现在某个象限中，即，均非0。也就是说，范数比范数更易获得“稀疏”解。
2）L2正则更快速的减小。好像是因为一方面，L1是绝对值函数，而L2是二次函数；另一方面因为求解方法的原因。具体的内容我也不是很清楚，有待于后期对于数量较大的数据实际操作才能的出结论。
3）L2正则有助于处理 条件数(condition number)不好的情况下矩阵求逆很困难的问题。
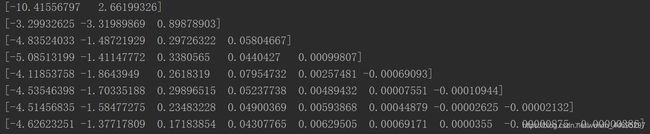
首先我们先理解一下什么是条件数。优化有两大难题，一是：局部最小值，二是：ill-condition病态问题。假设我们有个方程组AX=b，我们需要求解X。如果A或者b稍微的改变，会使得X的解发生很大的改变，那么这个方程组系统就是ill-condition的，反之就是well-condition的。我们具体举个例子吧：
上图我们可以看到，左边第三行我们稍微改变下系数矩阵A，可以看到结果的变化也很大。换句话来说，这个系统的解对系数矩阵A或者b太敏感了。A是我们的样本特征取值，b是样本真实值。A和b都是我们实验或者真实生活中记录的数据，在ill-condition状态下即使是发生一点小的偏差，对于参数的求解就会产生很大的误差，更不用说某些噪声的影响了。condition number就是拿来衡量ill-condition系统的可信度的。condition number衡量的是输入发生微小变化的时候，输出会发生多大的变化。也就是系统对微小变化的敏感度。condition number值小的就是well-conditioned的，大的就是ill-conditioned的。
如果方阵A是非奇异的，那么A的conditionnumber定义为：
如果一个矩阵的condition number在1附近，那么它就是well-conditioned的，如果远大于1，那么它就是ill-conditioned的，如果一个系统是ill-conditioned的，它的输出结果就不要太相信了。那L2正则如何有助于有助于处理 条件数(condition number)不好的情况呢？因为目标函数如果是二次的，对于线性回归来说，那实际上是有解析解的，求导并令导数等于零即可得到最优解为：（这里需要复习上一章线性模型多元线性回归的求解）
然而，如果当我们的样本X的数目比每个样本的维度还要小的时候，矩阵XTX将会不是满秩的，也就是
会变得不可逆，所以w*就没办法直接计算出来了。或者更确切地说，将会有无穷多个解（因为我们方程组的个数小于未知数的个数）。也就是说，我们的数据不足以确定一个解，如果我们从所有可行解里随机选一个的话，很可能并不是真正好的解，总而言之，我们过拟合了。
但如果加上L2规则项，就变成了下面这种情况，就可以直接求逆了：
具体的内容会在后面的求解过程中也会提及。
求解
Lasso：
由于L1范数用的是绝对值，导致LASSO的优化目标不是连续可导的，也就是说，最小二乘法，梯度下降法，牛顿法，拟牛顿法都不能用。L1正则化问题求解可采用近端梯度下降法（Proximal Gradient Descent，PGD）。
1）优化目标：
表示微分算子，若
可导，梯度
满足L-Lipschitz条件（利普希茨连续条件），即存在常数
，使得：
L-Lipschitz（利普希茨连续条件）定义：
对于函数
,
都存在
，即对于
。
2）泰勒展开：
梯度满足L-Lipschitz条件，则在
附近通过二阶泰勒展开式近似为：
const是与无关的常数，
表示内积。则容易看出上式的最小值取在：
3）简化优化问题：
这里若通过梯度下降法对（连续可导）进行最小化，则每一步下降迭代实际上等价于最小化二次函数
，推广到优化目标，可类似地得到每一步迭代公式：
即在每一步对进行梯度下降迭代的同时考虑L1范数最小化。可先令
，然后求解：
![{x_ {k + 1}} = \ mathop {\ arg \ min} \ limits_x \ left [{\ frac {L} {2} \ left \ | {x - z} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | x \ right \ |} _1}} \ right]](http://img.e-com-net.com/image/info8/143e62acc62444099b09400a3d3f85a3.gif)
令xi为x的第i个分量，将上式展开可以看到没有
（x≠j）的项，即x的各分量互不影响，所以优化目标有闭式解.这里对于上述优化问题求解需要用到Soft Thresholding软阈值函数，其解为：
对于本例，带入求解即得：
与
分别是
与
的第
个分量。因此，PGD能使LASSO和其他基于L1范数最小化的方法得以快速求解。
Ridge：
一种基于梯度下降，一种基于正规方程。
1）梯度下降：
2）正规方程：
也是前面部分L2正则有助于处理 条件数(condition number)不好的情况下矩阵求逆很困难的问题的补充。加入了L2正则化后，通过求导令导数为零：
我们得出了下面的结论。
所以。对于任意的实数
，
正定，从而可逆。保证回归公式一定有意义。
实例：
同时使用线性回归、Ridge、Lasso和ElasticNet，在1到8阶的拟合结果如下。可以看到线性回归在阶数越高的情况下，曲线振荡的程度也越强，越容易发生过拟合。而加入了正则化则可以很好的解决过拟合问题。
求解出的系数如下：
线性回归：
Ridge回归：
Lasso回归：
可以看到线性回归在7阶和8阶的时候系数急剧增加，曲线更加扭曲。Lasso求解出的参数已经及其接近于0了。
代码可在我个人GitHub上下载。https://github.com/Uncle-Yuanl/Machine-Learning
如果有任何问题以建议，欢迎留言交流。
参考博客：
正则化通俗化讲解。https://www.cnblogs.com/jianxinzhou/p/4083921.html
L1与L2特性。底下的评论也值得一看。https://blog.csdn.net/zouxy09/article/details/24971995
Lasso求解过程及Soft Thresholding软阈值函数证明。https://blog.csdn.net/BIT_666/article/details/80051737
Ridge求解过程：https://blog.csdn.net/u010725283/article/details/79212762