8. 基本分类模型
文章目录
- K近邻分类器(KNN)
-
- sklearn中的K近邻分类器
-
- 实例代码
- KNN的使用经验
- 决策树
-
- sklearn中的决策树
-
- 实例代码
- 决策树实例应用——购买行为预测
-
- 信息熵(entropy)
-
- 计算公式
- ID3算法
-
- 计算公式
- 训练样本
- 代码
- 决策树可视化
- 决策树的优缺点
- 实例代码
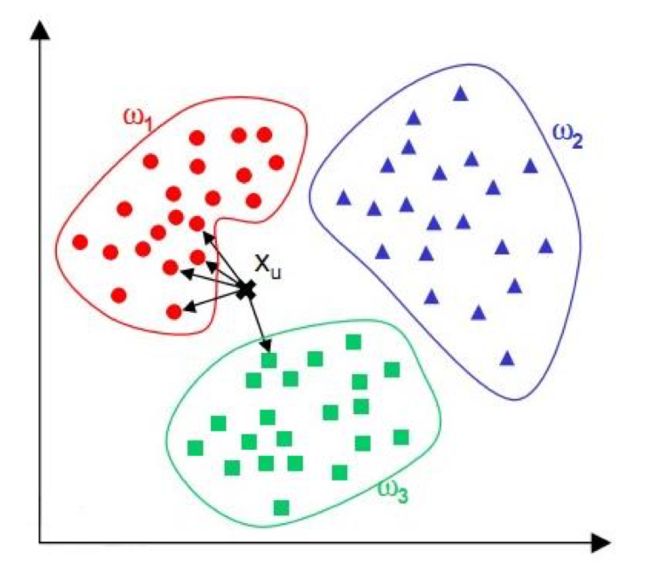
K近邻分类器(KNN)
通过计算待分类数据点,与已有数据集中的所有数据点的距离。取距离最小的前K个点,根据“少数服从多数“的原则,将这个数据点划分为出现次数最多的那个类别。
sklearn中的K近邻分类器
在sklearn库中,可以使用klearn.neighbors.KNeighborsClassifier创建一个K近邻分类器,主要参数有:
n_neighbors:用于指定分类器中K的大小(默认值为5)。weights:设置选中的K个点对分类结果影响的权重。默认值为平均权重“uniform”,可以选择“distance”代表越近的点权重越高,或者传入自己编写的以距离为参数的权重计算函数。algorithm:设置用于计算临近点的方法,因为当数据量很大的情况下计算当前点和所有点的距离再选出最近的k个点,这个计算量是很费时的,所以选项中有ball_tree、kd_tree和brute,分别代表不同的寻找邻居的优化算法。默认值为auto,表示根据训练数据自动选择。
实例代码
# 使用 import 语句导入 K 近邻分类器
from sklearn.neighbors import KNeighborsClassifier
# 创建一组数据 X 和它对应的标签 y
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
# 参数 n_neighbors 设置为 3,
# 即使用最近的3个邻居作为分类的依据,
# 其他参数保持默认值,并将创建好的实例赋给变量 neigh。
neigh = KNeighborsClassifier(n_neighbors=3)
# 调用 fit() 函数,
# 将训练数据 X 和 标签 y 送入分类器进行学习。
neigh.fit(X, y)
# 调用 predict() 函数,
# 对未知分类样本 [1.1] 分类,
# 可以直接并将需要分类的数据
# 构造为数组形式作为参数传入,
# 得到分类标签作为返回值。
print(neigh.predict([[1.1]]))
样例输出值是 0,表示K近邻分类器通过计算样本 [1.1] 与训练数据的距离, 取 0,1,2 这 3 个邻居作为依据,根据“投票法”最终将样本分为类别 0。
KNN的使用经验
在实际使用时,我们可以使用所有训练数据构成特征 X 和标签 y,使用 fit() 函数进行训练。在正式分类时,通过一次性构造测试集或者一个一个输入 样本的方式,得到样本对应的分类结果。有关 K 的取值:
- 如果较大,相当于使用较大邻域中的训练实例进行预测,可以减小估计误差,但是距离较远的样本也会对预测起作用,导致预测错误。
- 相反地,如果K较小,相当于使用较小的邻域进行预测,如果邻居恰好是噪声点,会导致过拟合。
- 一般情况下,K会倾向选取较小的值,并使用交叉验证法选取最优K值。
决策树
决策树是一种树形结构的分类器,通过顺序询问分类点的属性决定分类点最终的类别。通常根据特征的信息增益或其他指标,构建一颗决策树。在分类时,只需要按照决策树中的结点依次进行判断,即可得到样本所属类别。
决策树本质上是寻找一种对特征空间上的划分,旨在构建一个训练数据拟合的好,并且复杂度小的决策树。
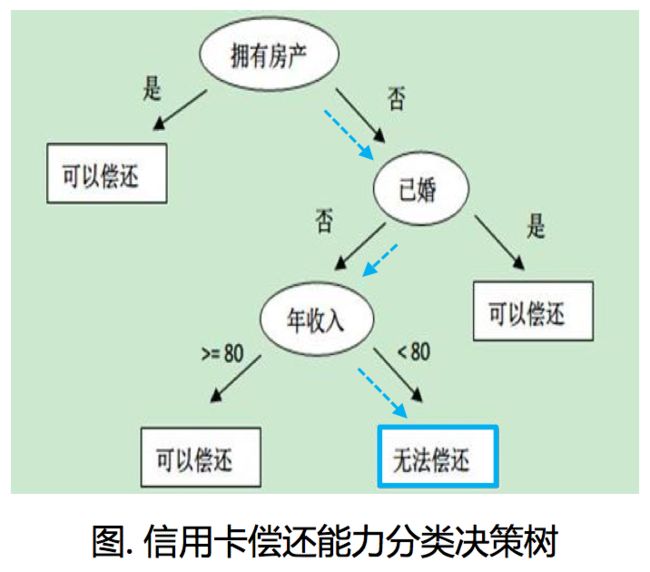
例如,根据右图这个构造好的分类决策树, 一个无房产,单身,年收入55K的人的会被归入无法偿还信用卡这个类别。
sklearn中的决策树
在sklearn库中,可以使用sklearn.tree.DecisionTreeClassifier创建一个决策树用于分类,其主要参数有:
criterion:用于选择属性的准则,可以传入“gini”代表基尼系数,或者“entropy”代表信息增益。max_features:表示在决策树结点进行分裂时,从多少个特征中选择最优特征。可以设定固定数目、百分比或其他标准。它的默认值是使用所有特征个数。
在实际使用中,需要根据数据情况,调整DecisionTreeClassifier类中传入的参数,比如选择合适的criterion,设置随机变量等。
实例代码
# 导入 sklearn 内嵌的鸢尾花数据集
from sklearn.datasets import load_iris
# 导入决策树分类器
from sklearn.tree import DecisionTreeClassifier
# 导入计算交叉验证值的函数 cross_val_score
from sklearn.model_selection import cross_val_score
# 使用默认参数,
# 创建一颗基于基尼系数的决策树,
# 并将该决策树分类器赋值给变量 clf
clf = DecisionTreeClassifier()
# 将鸢尾花数据赋值给变量 iris
iris = load_iris()
# 将决策树分类器做为待评估的模型,
# iris.data鸢尾花数据做为特征,
# iris.target鸢尾花分类标签做为目标结果,
# 通过设定cv为10,使用10折交叉验证。
# 得到最终的交叉验证得分。
print(cross_val_score(clf, iris.data, iris.target, cv=10))
使用方法类似
# 利用 fit() 函数训练模型
clf.fit(X, y)
# 使用 predict() 函数
clf.predict(x)
决策树实例应用——购买行为预测
信息熵(entropy)
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。直到1948年,香农提出了“信息熵”的概念,才解决了对信息的量化度量问题。
计算公式
H ( x ) = − ∑ x P ( x ) log 2 P ( x ) H(x)=-\sum_{x}P(x)\log_{2}P(x) H(x)=−x∑P(x)log2P(x)
变量的不确定性越大,熵也就越大。
ID3算法
通过信息获取量(Information Gain)来确定属性判断节点的位置。
计算公式
从节点A获得的信息等于没有节点A时的信息熵减去有A时的信息熵的差。
G a i n ( A ) = I n f o ( D ) − I n f o A ( D ) Gain(A)=Info(D)-{Info}_A(D) Gain(A)=Info(D)−InfoA(D)
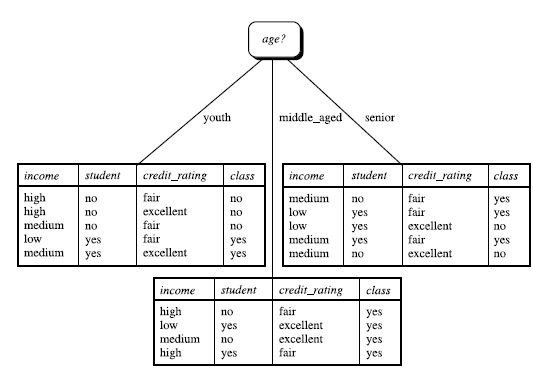
训练样本
AllElectronics.csv
RID,age,income,student,credit_rating,class_buys_computer
1,youth,high,no,fair,no
2,youth,high,no,excellent,no
3,middle_aged,high,no,fair,yes
4,senior,medium,no,fair,yes
5,senior,low,yes,fair,yes
6,senior,low,yes,excellent,no
7,middle_aged,low,yes,excellent,yes
8,youth,medium,no,fair,no
9,youth,low,yes,fair,yes
10,senior,medium,yes,fair,yes
11,youth,medium,yes,excellent,yes
12,middle_aged,medium,no,excellent,yes
13,middle_aged,high,yes,fair,yes
14,senior,medium,no,excellent,no
最后一列的信息熵
I n f o ( D ) = − 9 14 log 2 ( 9 14 ) − 5 14 log 2 5 14 = 0.940 b i t s Info(D)=-\frac{9}{14}\log_{2}(\frac{9}{14})-\frac{5}{14}\log_{2}{\frac{5}{14}}=0.940 bits Info(D)=−149log2(149)−145log2145=0.940bits
加上age后的信息熵
I n f o a g e ( D ) = − 5 14 × ( − 2 5 log 2 2 5 − 3 5 log 2 3 5 ) − 4 14 × ( − 4 4 log 2 4 4 − 0 4 log 2 0 4 ) − 5 14 × ( − 3 5 log 2 3 5 − 2 5 log 2 2 5 ) = 0.694 b i t s {Info}_{age}(D)=-\frac{5}{14}\times (-\frac{2}{5}\log_{2}\frac{2}{5}-\frac{3}{5}\log_{2}\frac{3}{5})-\frac{4}{14}\times (-\frac{4}{4}\log_{2}\frac{4}{4}-\frac{0}{4}\log_{2}\frac{0}{4})-\frac{5}{14}\times (-\frac{3}{5}\log_{2}\frac{3}{5}-\frac{2}{5}\log_{2}\frac{2}{5})=0.694 bits Infoage(D)=−145×(−52log252−53log253)−144×(−44log244−40log240)−145×(−53log253−52log252)=0.694bits
解释:5个年轻人中3个没买,2个买了。4个中年人全买了。5个老年人中3个买了2个没买。
G a i n ( a g e ) = I n f o ( D ) − I n f o a g e ( D ) = 0.246 b i t s Gain(age)=Info(D)-{Info}_{age}(D)=0.246 bits Gain(age)=Info(D)−Infoage(D)=0.246bits
即仅以年龄作为依据得到的信息增益为0.246bits。
类似地还可以算出
G a i n ( i n c o m e ) = 0.029 b i t s Gain(income)=0.029bits Gain(income)=0.029bits
G a i n ( s t u d e n t ) = 0.151 b i t s Gain(student)=0.151bits Gain(student)=0.151bits
G a i n ( c r e d i t _ r a t i n g ) = 0.048 b i t s Gain(credit\_rating)=0.048bits Gain(credit_rating)=0.048bits
所以选择age作为第一个节点。目前的决策树如下图所示:
重复以上的步骤,直到获得完整的决策树。
代码
import csv
from sklearn import tree
from sklearn import preprocessing
from sklearn.feature_extraction import DictVectorizer
'''读取文件'''
allElectronicsData = open('AllElectronics.csv')
reader = csv.reader(allElectronicsData)
headers = next(reader) # 第一行表头 ['RID', 'age', ...]
# print(headers)
'''对数据进行预处理'''
# feature_list 列表中的元素是一个字典,每个字典包含了一个样本的所有特征
# label_list 每一个样本的标签:是否买了电脑
feature_list = []
label_list = []
for row in reader: # 每一行
# 加入标签
label_list.append(row[len(row) - 1])
# 将一行的信息加入rowDict中
row_dict = {}
for i in range(1, len(row)-1):
row_dict[headers[i]] = row[i]
# 将row_dict加入featureList
feature_list.append(row_dict)
# print(feature_list)
# print(label_list)
'''将特征向量化'''
# featureList是一个装有字典的列表,这种形式的数据可以通过DictVectorizer()
# 完成向量化,转化后特征中只含有0和1,
vec = DictVectorizer()
# 新的特征
dummy_X = vec.fit_transform(feature_list).toarray()
# 新的特征对应的原来的特征
# print(vec.get_feature_names())
# print("dummy_X: \n" + str(dummy_X))
'''将标签向量化'''
lb = preprocessing.LabelBinarizer()
dummy_Y = lb.fit_transform(label_list)
print("dummy_Y: \n" + str(dummy_Y))
'''使用决策树进行分类'''
clf = tree.DecisionTreeClassifier(criterion='entropy') # criterion='entropy'使用ID3方法
clf = clf.fit(dummy_X, dummy_Y)
print("clf: " + str(clf))
'''模型可视化'''
# 安装了Graphviz后可以使用
# dot -T pdf <文件名> -o output.pdf
# 生成决策树
with open("allElectronicInformationGain.dot", 'w') as f:
f = tree.export_graphviz(clf, feature_names=vec.get_feature_names(), out_file=f)
'''预测'''
# 取出训练集的第一行
oneRowX = dummy_X[0, :]
# 把第一行的数据改动一下
newRowX = oneRowX
newRowX[0] = 1
newRowX[2] = 0
# 预测这个人是否买电脑
predictedY = clf.predict(newRowX)
print("predictedY: " + str(predictedY))
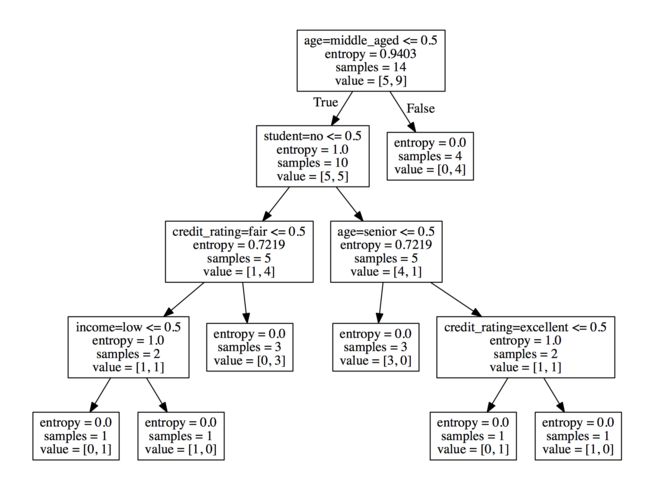
决策树可视化
决策树的优缺点
优点:直观,便于理解,小规模数据集有效。
缺点:处理连续变量不好;类别较多时,错误增加的比较快;可规模性一般。
#朴素贝叶斯
朴素贝叶斯分类器是一个以贝叶斯定理为基础 的多分类的分类器。
朴素贝叶斯是典型的生成学习方法,由训练数据学习联合概率分布,并求得后验概率分布。
朴素贝叶斯一般在小规模数据上的表现很好,适合进行多分类任务。
p ( A ∣ B ) = p ( B ∣ A ) ⋅ p ( A ) P ( B ) p(A|B)=\frac{p(B|A)\cdot p(A)}{P(B)} p(A∣B)=P(B)p(B∣A)⋅p(A)
##sklearn中的朴素贝叶斯
在sklearn库中,实现了三个朴素贝叶斯分类器.
| 分类器 | 描述 |
|---|---|
naive_bayes.GussianNB |
高斯朴素贝叶斯 |
naive_bayes.MultinomialNB |
针对多项式模型的朴素贝叶斯分类器 |
naive_bayes.BernoulliNB |
针对多元伯努利模型的朴素贝叶斯分类器 |
区别在于假设某一特征的所有属于某个类别的观测值符合特定分布,如,分 类问题的特征包括人的身高,身高符合高斯分布,这类问题适合高斯朴素贝叶斯。
在sklearn库中,可以使用sklearn.naive_bayes.GaussianNB创建一个高斯 朴素贝叶斯分类器,其参数有:
priors:给定各个类别的先验概率。如果为空,则按训练数据的实际情况进行统计。如果给定先验概率,则在训练过程中不能更改。
实例代码
# 导入 numpy 库
import numpy as np
# 导入朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
# 构造训练数据 X 和 y
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
# 使用默认参数创建一个高斯朴素贝叶斯分类器,
# 并将该分类器赋给变量 clf
clf = GaussianNB(priors=None)
# 类似的,使用 fit() 函数进行训练,
# 并使用 predict() 函数进行预测,
# 得到预测结果为 1。
# (测试时可以构造二维数组达到同时预测多个样本的目的)
clf.fit(X, Y)
print(clf.predict([[-0.8, -1]]))