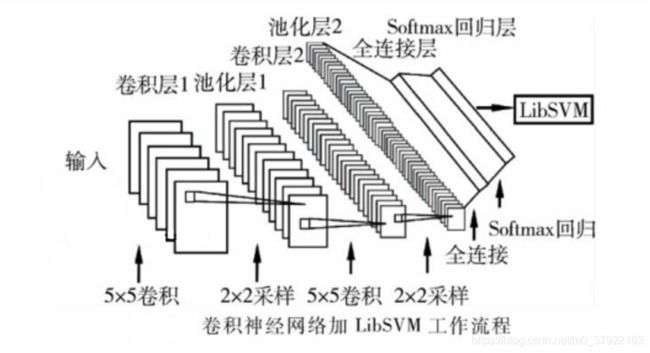
基于卷积神经网络（cnn)与支持向量机(svm)结合的猫狗识别

猫狗识别一直都是模式识别的入门级数据集，因为其数据易采集，贴近生活，数据特征与图像规模的关联并不是特别大，预处理时图像特征容易保存，很多初学者都是以此作为提升使用各种分类器熟练度的数据集。本次实验也是想通过使用这个数据集来测试卷积网络与支持向量机相结合的效果，数据集本生并没有特殊的意义。
卷积网络是神经网路家族一个长老级的存在，在视觉，图像等领域都有广泛的应用，其本身价值在于通过卷积计算可以有效地省去特征工程这个环节，再次基础上还衍生了很多新型的如VGG，Inception,ResNet等网络结构，在各大比赛，会议上出尽风头。本文利用的是最传统的LeNet5层结构，主要原因在于我的电脑跑不起更加深层的网络，同时除了ResNet,过深的网络结构往往会出现梯度爆炸或者梯度消失等问题，loss值往往会变成nan值。同时，这次实验的目的主要目的在于体现卷积网络和支持向量机结合的价值，因此使用简单易训练的LeNet是再合适不过了。
支持向量机（SVM) 是机器学习的老成员了，在神经网路风靡全球之前，一度都是学者的宠儿，在分类和回归问题上都有着大量的实践与应用，即便在神经网路风靡的今天，由于他的稳定性和易植入性依旧焕发着强劲的生命力。
本文试图将卷积神经网络的优势与支持向量机的稳定性相结合，利用训练好的卷积层与池化层提取图片的特征，放入支持向量机中进行训练，进行分类操作。其意义在于利用SVM来替换卷积网络中的全连接层，经实验验证，效果会提升2%-3%，这是一个很可观的提升，并且具备着广泛的意义，在各项其他环境下都能起到不错的效果。

CNN和SVM结合的意义

使用卷积作为特征提取以及SVM作为分类器的具体理由如下：
1.由于卷积和池化计算的性质，使得图像中的平移部分对于最后的特征向量是没有影响的。从这一角度说，提取到的特征更不容易过拟合。而且由于平移不变性，所以平移字符进行变造是无意义的，省去了再对样本进行变造的过程。
2.CNN抽取出的特征要比简单的投影、方向，重心都要更科学。不会让特征提取成为最后提高准确率的瓶颈、天花板。
3.可以利用不同的卷积、池化和最后输出的特征向量的大小控制整体模型的拟合能力。在过拟合时可以降低特征向量的维数，在欠拟合时可以提高卷积层的输出维数。相比于其他特征提取方法更加灵活。
4.非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射；
5.对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心；
6.支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。
识别效果如下：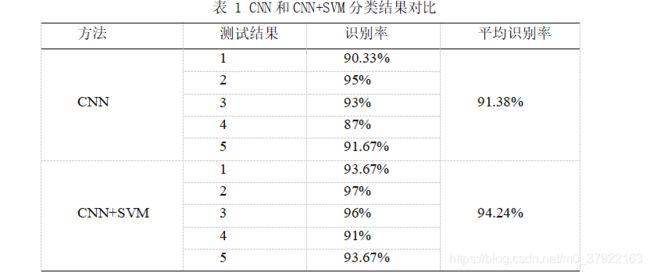

局部代码（cnn)：

sess = tf.InteractiveSession()
def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev = 0.05)  #截断的正态分布，标准差stddev
    return tf.Variable(initial)
# 偏置参数初始化
def bias_variable(shape):
    initial = tf.constant(0.1, shape = shape)
    return tf.Variable(initial) 
# 定义卷积层
def conv2d(x, W):
    # stride的四个参数：[batch, height, width, channels], [batch_size, image_rows, image_cols, number_of_colors]
    # height, width就是图像的高度和宽度，batch和channels在卷积层中通常设为1
    return tf.nn.conv2d(x, W, strides = [1, 1, 1, 1], padding = 'SAME') 
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize = [1, 2, 2, 1], strides = [1, 2, 2, 1], padding = 'SAME')

xs = tf.placeholder(tf.float32, [None, 6400])
ys = tf.placeholder(tf.float32, [None, 2])
keep_prob = tf.placeholder(tf.float32)

x_image = tf.reshape(xs, [-1, 80, 80, 1])#  -1, 28, 28, 1

#print(x_image.shape)

# 卷积层一

# patch为5*5，in_size为1，即图像的厚度，如果是彩色，则为3，32是out_size，输出的大小-》32个卷积和（滤波器）

W_conv1 = weight_variable([9, 9, 1, 32])
b_conv1 = bias_variable([32])
# ReLU操作，输出大小为28*28*32

h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# Pooling操作，输出大小为14*14*32
h_pool1 = max_pool_2x2(h_conv1)


# 卷积层二

# patch为5*5，in_size为32，即图像的厚度，64是out_size，输出的大小

W_conv2 = weight_variable([9, 9, 32, 64])
b_conv2 = bias_variable([64])
# ReLU操作，输出大小为14*14*64
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# Pooling操作，输出大小为7*7*64
h_pool2 = max_pool_2x2(h_conv2)

 

# 全连接层一
W_fc1 = weight_variable([20 * 20 * 64, 640])
b_fc1 = bias_variable([640])
# 输入数据变换
h_pool2_flat = tf.reshape(h_pool2, [-1, 20 * 20 * 64])  #整形成m*n,列n为7*7*64
# 进行全连接操作
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)  # tf.matmul
# 防止过拟合，dropout
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)


# 全连接层二
W_fc2 = weight_variable([640, 2])
b_fc2 = bias_variable([2])

prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
# 计算loss
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(tf.clip_by_value(prediction,1e-8,1.0))))
# 神经网络训练
train_step = tf.train.AdamOptimizer(0.0001).minimize(cross_entropy) #0.0001

# 定义Session
sess = tf.Session()

init = tf.global_variables_initializer()
# 执行初始化
sess.run(init)

局部代码（svm)

model = svm_train(train_label,x_temp,'-t 3 -c 1 -w1 1 ')
predict_label,accuracy,dec_values = svm_predict(test_label,x_temp2,model)

完整数据和代码：//download.csdn.net/download/m0_37922163/11965734