sklearn机器学习:决策树案例
系列文章目录
文章目录
- 系列文章目录
- 一、决策树原理
-
- 1.1 定义
- 1.2 优点
- 1.3 缺点
- 二、分类树
-
- 2.1 函数语法
- 2.2 案例
- 三、回归树案例
-
- 3.1 函数语法
- 3.2 案例
一、决策树原理
1.1 定义
决策树是一种用来 classification (分类)和 regression(回归) 的无参监督学习方法。其目的是创建一种模型从数据特征中学习简单的决策规则来预测一个目标变量的值
1.2 优点
- 便于理解和解释。树的结构可以可视化出来。
- 训练需要的数据少。其他机器学习模型通常需要数据规范化,比如构建虚拟变量和移除缺失值。
- 决策树的开销和决策树导入的训练集数目呈指数关系。
- 能够处理数值型数据和分类数据
- 能够处理多路输出的问题
- 使用白盒模型。如果某种给定的情况在该模型中是可以观察的,那么就可以轻易的通过布尔逻辑来解释这种情况。
- 可以通过数值统计测试来验证该模型。(解释模型的可靠性)
- 即使该模型假设的结果与真实模型所提供的数据有些违反,其表现依旧良好。
1.3 缺点
- 过拟合:决策树模型容易产生一个过于复杂的模型,泛化性能可能会很差。剪枝、设置叶节点所需的最小样本数或设置数的最大深度是避免出现该问题有效方法。
- 决策树可能是不稳定的,因为数据中的微小变化可能会导致完全不同的树生成。这个问题可以通过决策树的集成来得到缓解。
- 决策树学习算法是基于启发式算法,学习一棵最优决策树通常是一个NP难问题。例如在每个节点进行局部最优决策的贪心算法,这样的算法不能保证返回全局最优决策树。这个问题可以通过集成学习来训练多棵决策树来缓解,这多棵决策树一般通过对特征和样本有放回的随机采样来生成。
- 数据平衡:如果某些类在问题中占主导地位会使得创建的决策树有偏差。因此,我们建议在拟合前先对数据集进行平衡
二、分类树
2.1 函数语法
官方解释:决策分类树
sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0)
| 参数 | 含义 |
|---|---|
| criterion | 节点分裂效果的量化指标,默认gini(基尼系数);可选择:entropy(信息熵)和gini和log_loss |
| splitter | 用于在每个节点上选择拆分的策略。支持的策略是“best”选择最佳拆分,“random”选择最佳随机拆分。 |
| max_depth | 树的最大深度.;若为None,则节点一直分裂,直到无法继续分裂,或者叶子节点包含的样本数目小于min_samples_split |
| min_samples_split | 一个节点分枝所需要的最小样本数目: 如果是int,那么考虑min_samples_split作为最小值。如果是float,那么min_samples_split是一个分数,ceil(min_samples_split * n_samples)是每次拆分的最小样本数。 |
| min_samples_leaf | 一个节点分枝后,分裂的节点所包含的最小样本数目。如果是int,那么考虑min_samples_leaf作为最小值。如果是float,那么min_samples_leaf是一个分数,ceil(min_samples_leaf * n_samples)是每个节点的最小样本数。 |
| min_weight_fraction_leaf | 叶节点上所需的(所有输入样本的)权重总和的最小加权分数。当没有提供sample_weight时,样本具有相等的权值 |
| max_features | 限制分枝时考虑的特征个数 。如果是int,那么考虑每次拆分时的max_features特性。如果是float,那么max_features是一个分数,max(1, int(max_features * n_features_in_))特征在每次拆分时都被考虑。如果" auto “,那么max_features=sqrt(n_features)。如果” sqrt “,那么max_features=sqrt(n_features)。如果” log2 ",那么max_features=log2(n_features)。如果为None,则max_features=n_features。 |
| random_state | 如果准则的改进对于几个分割是相同的,并且必须随机选择一个分割,则情况就是如此。为了在拟合过程中获得确定性行为,random_state必须固定为一个整数。 |
| max_leaf_nodes | 最大的叶子节点数目 |
| min_impurity_decrease | 限制信息增益的大小,信息增益小于设定数值的分枝不会发生。 |
| class_weight | 可以采用“balanced”模式使用y的值自动调整权重,权重与输入数据中的类频率成反比,如n_samples / (n_classes * np.bincount(y)) |
- criterion:通常就使用基尼系数;数据维度很大,噪音很大时使用基尼系数;维度低,数据比较清晰的时候,信息熵和基尼系数没区别;当决策树的拟合程度不够的时候,使用信息熵;两个都试试,不好就换另外一个
- max_depth:实际使用时,建议从=3开始尝试,看看拟合的效果再决定是否增加设定深度
- min_samples_leaf:搭配max_depth使用,这个参数的数量设置得太小会引起过拟合,设置得太大就会阻止模型学习数据。一般来说,建议从=5开始使用。如果叶节点中含有的样本量变化很大,建议输入浮点数作为样本量的百分比来使用。
属性列表:
| 属性 | 含义 |
|---|---|
| classes_ | 类标签(单个输出问题),或类标签数组列表(多个输出问题)。 |
| feature_importances_ | 特征权重 |
| max_features_ | max_features的推断值。 |
| n_classes_ | 类的数量(针对单个输出问题),或包含每个输出的类的数量的列表(针对多个输出问题)。 |
| n_features_in_ | fit时看到的特征数目 |
| feature_names_in_ | fit时看到的特征名称 |
| n_outputs_ | fit时output的数目 |
| tree_ | 底层Tree对象 |
2.2 案例
数据集采用的是:sklearn.datasets中的wine数据集,在这里我把它导出为了csv进行后续训练。
from sklearn import tree
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
import pandas as pd
import graphviz
#读取数据
wine=pd.read_csv(r"D:\ml-learn\code\decision-tree\wine.csv")
#特征和标签
wine_features,wine_label=wine.iloc[:,:13],wine.iloc[:,13:14]
#划分数据集
Xtrain,Xtest,Ytrain,Ytest=train_test_split(wine_features,wine_label,test_size=0.3)
#构建模型
clf = tree.DecisionTreeClassifier(criterion="entropy",
splitter="best",
max_depth=5,
min_samples_split=0.15,
min_samples_leaf=0.05,
random_state=1,
class_weight="balanced")
#训练模型
clf = clf.fit(Xtrain, Ytrain)
#决策树属性
#决策树标签种类
classes=clf.classes_
#特征重要性权重
feature_importance=clf.feature_importances_
#最大特征数目
clf.max_features_
#标签的种类数目
clf.n_classes_
#输入特征数目
clf.n_features_in_
#输出标签数目
clf.n_outputs_
#决策树对象
clf.tree_
#决策树方法
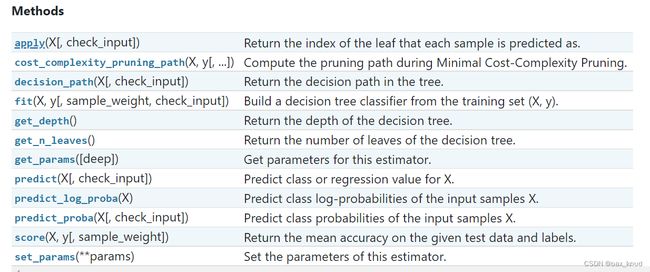
#apply:返回样本预测类别所在的叶子节点
clf.apply(Xtest)
#计算最小成本复杂度修剪过程中的修剪路径。
clf.cost_complexity_pruning_path(Xtest,Ytest)
#返回决策路径
clf.decision_path(Xtest)
#决策树深度
clf.get_depth()
#决策树叶子节点数目
clf.get_n_leaves()
#决策树训练参数
clf.get_params
#获取预测值
clf.predict(Xtest)
#获取预测值的log-probabilities :范围在-inf到0
clf.predict_log_proba(Xtest)
#预测每一类的可能性:范围在0-1
clf.predict_proba(Xtest)
#测试集得分:准确率
clf.score(Xtest,Ytest)
#绘制一个决策树,并保存pdf
dot_data = tree.export_graphviz(clf,
out_file=None,
feature_names=wine_features.columns,
class_names=["class1","class2","class3"],
filled=True, rounded=True,special_characters=True)
graph = graphviz.Source(dot_data)
graph.render(r"D:\ml-learn\code\decision-tree\wine")
三、回归树案例
3.1 函数语法
官方函数说明:DecisionTreeRegressor
sklearn.tree.DecisionTreeRegressor(*, criterion='squared_error', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, ccp_alpha=0.0)
回归树和分类树主要不同的参数在于criterion
criterion表示回归树衡量分枝质量的指标,支持的标准有三种:
- 输入"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失
- 输入“friedman_mse”使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
- 输入"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失
方法区别:回归树的接口score返回的是R平方,并不是MSE
3.2 案例
#回归树案例:
from sklearn.model_selection import cross_val_score
from sklearn import tree
from sklearn.model_selection import train_test_split
import graphviz
import pandas as pd
#读取数据
boston=pd.read_csv(r"D:\ml-learn\code\decision-tree\boston_house_prices.csv")
boston_features,boston_target=boston.iloc[:,:13],boston.iloc[:,13:]
#划分数据集
Xtrain,Xtest,Ytrain,Ytest=train_test_split(boston_features,boston_target,test_size=0.3)
#构建回归树
regressor=tree.DecisionTreeRegressor(random_state=1,max_depth=5)
#训练回归树
regressor=regressor.fit(Xtrain,Ytrain)
#交叉验证
cross_val_score(regressor,Xtest,Ytest, cv=10,scoring = "neg_mean_squared_error")
# 回归树属性
#特征重要性权重
regressor.feature_importances_
#最大特征数目
regressor.max_features_
#标签的种类数目
regressor.n_classes_
#输入特征数目
regressor.n_features_in_
#输出标签数目
regressor.n_outputs_
#回归树对象
regressor.tree_
#回归树方法
#apply:返回样本预测类别所在的叶子节点
regressor.apply(Xtest)
#计算最小成本复杂度修剪过程中的修剪路径。
regressor.cost_complexity_pruning_path(Xtest,Ytest)
#返回决策路径
regressor.decision_path(Xtest)
#决策树深度
regressor.get_depth()
#决策树叶子节点数目
regressor.get_n_leaves()
#决策树训练参数
regressor.get_params
#获取预测值
regressor.predict(Xtest)
#测试集得分:准确率
regressor.score(Xtest,Ytest)
#绘制一个决策树,并保存pdf
dot_data = tree.export_graphviz(regressor,
out_file=None,
feature_names=boston_features.columns,
filled=True, rounded=True,special_characters=True)
graph = graphviz.Source(dot_data)
graph.render(r"D:\ml-learn\code\decision-tree\boston")