软件工程经济学期末复习第五章

软件工程经济学期末复习总结

第5章 软件生产过程经济分析
软件生产过程：
规划、需求分析、概要设计、详细设计、编码、系统集成、测试、交付
本章研究主要内容：

生产过程的规模效应
投入要素与产出关联变动的规律
劳动生产率的提高

生产函数
是宏观经济学和微观经济学理论中的一个重要概念
是研究系统规模变化对产出的影响和最优化经济效果的基础
反映生产过程中投入要素与其可能生产的最大产量之间的依存关系 的数学表达式
Y=F(K,L,N,O,t)
Y为产出量，如宏观经济中的GDP、工业总产值，微观经济中的企业产量、销售收入等；
K为资本
L为劳动
N为土地
O为组织管理
t为时间或工期
简化为：Y=F(K,L,t)
C-D生产函数
西方学者在采用计量经济学的有关统计法的研究中提出了多种形式的生产函数，从不同的侧面反映了西方国家生产过程中的工程经济行为。
由美国数学家柯布和经济学家道格拉斯提出的C-D函数形式如下：
Y=ALαKβ

Y为产出量；
L为劳动力投入；
K为资本投入；
A为除劳动与资本要素外其他对产出Y的总影响。

分别对L和K求偏导，得：

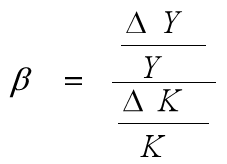
 称为劳动力对产出的弹性系数，表示在其他条件不变的情况下，劳动力增加百分之一会使产出变化的百分比；
 称为资本对产出的弹性系数，表示在其他条件不变的情况下，资本增加百分之一会使产出变化的百分比；
生产函数一般都满足如下特性:
资本与劳动力的边际产出均为正值，即有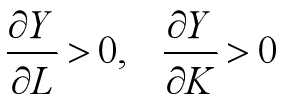
其经济含义为:劳动力（或资本）投入量不变的情况下，资本（或劳动力）的增加将导致产出量的增加。
边际产量递减，即有

其经济含义为:当其他生产要素固定不变时，随着某一要素投入量的增加，边际产量将逐渐减少。
生产函数具有非负性，且总产量是生产要素组合的结果，即总产出为正值，单一要素的投入不能获得产出。即有
Y=F(K,L,t)>0 Y=F(K,0,t)=0 Y=F(0,L,t)=0
规模经济（规模报酬）
是微观经济学研究的一个主要问题
表示当生产规模变化时，对产出的影响程度。
规模报酬一般有三种情况：
当全部生产要素按某种配合方式以相同比例增加时，

• 若 Y=F(λK,λL,t) > λF(K，L,t),
  则称该生产活动呈规模报酬递增或规模经济；
• 若 Y=F(λK,λL,t) < λF(K，L,t) ，
  则称该生产活动呈规模报酬递减或非规模经济；
• 若 Y=F(λK,λL,t) = λF(K，L,t) ，
  则称该生产活动呈规模报酬固定
  Y=F(K,L,t)= ALαKβ
  F(λK, λL, t)=A(λL)α(λK)β
  = λ α+ βAL α K β
  = λ α+ βY
  因此对C-D函数容易验证得以下结论：

若 α+ β>1，则称该生产活动呈规模报酬递增或规模经济；
若 α+ β<1，则称该生产活动呈规模报酬递减或非规模经济；
若 α+ β=1，则称该生产活动呈规模报酬固定

弹性系数求解
C-D生产函数是一种较为普遍的生产过程中的生产过程规律描述。
但对于不同的企业（部门和地区），由于其外部环境与内部条件的不同，故产出对劳动力或资本的变化反映程度不同，即 α与 β不同。
求解思路：
收集特定企业（部门和地区）的数据序列，将二元非线性函数转化为二元线性函数求解
弹性系数求解
注意到(5.2)式中实际上Y、K、L、A均为时间t的函数，不妨设为yt，kt，lt，a(t)，则有

yt=a(t)·ltα·ktβ
对上式两端分别求对数有
lnyt=lna(t)+α lnlt+β lnkt
令Yt=lnyt，A(t)=lna(t)，L(t)=lnlt，K(t)=lnkt，则有
Yt=A(t)+α·L(t)+β·K(t)

软件生产函数
美国软件工程专家( L.H. Putnum )

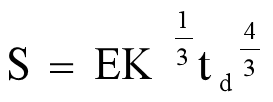
S为软件生产规模或源代码程序量（单位：NCSS ） ；
K为软件项目在生存期内投入的总工作量（单位：人年）
td为软件项目投入的人力峰值，通常为交付期或工期（单位：年）
软件生产函数的三个特性：
软件工作量或交付工期的边际生产量均为正
软件工作量的边际生产量递减；交付工期的边际生产量递增；
软件生产函数具有非负性
根据软件函数中弹性系数之和大于1，可知软件生产活动具有规模报酬递增效应。
软件生产率的定义：
==每个人月所交付的源代码程序量， 单位：NCSS/PM ==
软件生产效率的影响因素：
组织、管理因素
技术因素
提高生产效率的常用措施：
提高团队工作的业务规范、编程规范
采用较为先进的软件工具
部分功能采用商业软件包
改编现有的已熟悉软件的部分功能
采用软件构件技术、多版本技术、软件复用技术
建立科学、合理的激励、约束机制
对人员的选择采用如下五原则：顶级天才、任务匹配、职业发展、团队平衡、逐步淘汰原则
软件生产过程经济分析–分析什么？
软件生产系统内在经济要素关联及其动态发展规律。
经济要素：生产规模、开发难度、人力工作量（累计工作量、人力峰值）、费用、劳动生产率、环境因子、交付期等
例如：劳动生产率和生产规模、开发难度、环境因子之间的关联；开发难度和总工作量、交付期之间的关联；人力峰值的到达时间等。
如何分析？—— 建立系统动力学方程
软件生产系统动力学方程
英国软件工程学家诺顿提出了Noder-Rayleigh Model
建立模型基础：a、假设（基于客观统计数据上的一种经验）
b、统计分析

诺顿-瑞利模型 Noder-Rayleigh Model
模型假设如下：
开发项目中需要投入的总工作量K为有限；
C(t)在项目开始时为零，即C(0)=0,然后单调增长到K；
任何时刻开发项目组投入的人力数m(t)与尚待解决的问题（或尚需投入）的累计人力工作量成正比；
在项目生存周期中，项目开发人员由于不断学习，因而其开发效率可用关于时间t的学习函数p(t)来描述，是时间t的线性增函数，其m(t)与p(t)成正比。
----由假设得下列人力投入的系统动力学方程：
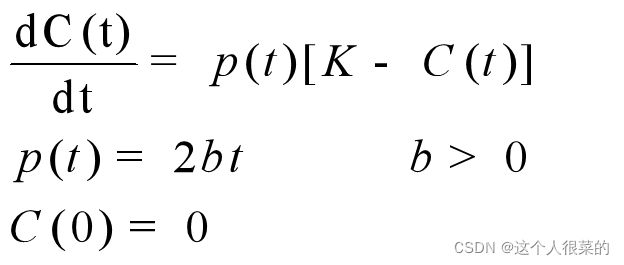求解微分方程得：
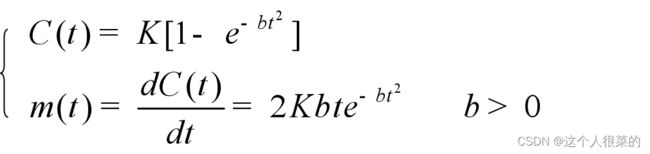因为函数m(t)具有概率论中瑞利分布函数的形式，故m(t)称为诺顿-瑞利曲线。
提出问题：
哪一时刻达到开发人员的峰值？
因此需要研究函数 m(t)

通过
，求得N-R曲线在
点时取得最大值。

显然，m(t0)即为软件生存周期中的开发人员的峰值。
由此可知，对于不同的b值（b>0）和K值，N-R曲线均为具有单峰值且自左向右由单调增到单调降的曲线。

Putnum 通过对英美大量软件项目的研究，得到了一些统计规律：
结论1：
软件项目的开发难度与生存周期内投入的总工作量K成正比，与交付期td2成反比。
D为软件工程开发难度系数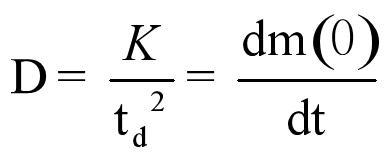
结论2：
对于具有统一项目开发特性的软件工程，尽管随着项目规模的增大，K和td均将增大，然而K/td3则基本稳定在某一常数周围，而不同开发属性的项目其常数不同。
8,软件是一个与其他系统有多个接口和交互功能的全新软件
D0= 15，软件是一个独立系统
27，软件是从其他已开发的软件基础上建立的系统
引入参数D0， D0为人力增长率

应用：
结论3：

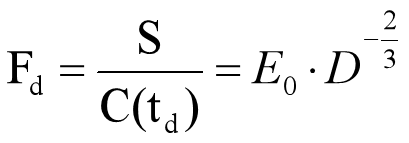
— Fd为软件项目的劳动生产率，E0为软件项目开发环境的技术状态。
公式的经济含义：
难度越大，劳动生产率越低下
在同样难度下，不同的开发环境、技术状态（如开发方法、开发工具、项目管理状态），亦将直接影响软件项目的劳动生产率。

环境因子
反映开发机构个性（开发风格和习惯）的工程经济参数
由开发环境、技术状态（如开发方法、开发工具和设备管理状况等）所决定。
确定环境因子的方法：

• 类比法
• 统计分析法
  不同规模软件工程经济分析表明：
  随着规模的加大，软件工程经济项目的人力资源组织及其管理有较大区别。
  随着规模的增大，开发机构的人力资源分成：
  项目开发任务组
  ----开发的基本任务：规划、分析、设计、编码及审查与测试
  项目支持任务组
  应用学科领域知识的支持
  计算机网络与通信设备的使用与维护支持
  工程计划网络的设计、跟踪与控制
  文本提供、质量保证与配置管理
  资源控制、任务跟踪协调与进程监控
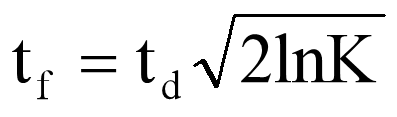  此公式表明了该软件项目理论生命周期tf与交付工期td、投入人力费用总量K之间的数量关系。
  小结：
  通过本章的学习：
  认识到项目开发过程中历史数据序列的重要性
  理解软件生产过程经济分析的过程：
• 确定所要研究的问题
• 建立数学模型（函数）
• 研究函数
• 用研究得出的结论来指导实际生产过程，即控制与管理