赫夫曼树及赫夫曼编码

上一篇 字典树
下一篇 B树及其实现

赫夫曼树

简介

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)

赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近

路径：
在一棵树中，从一个结点到另一个结点所经过的所有结点，被我们称为两个结点之间的路径
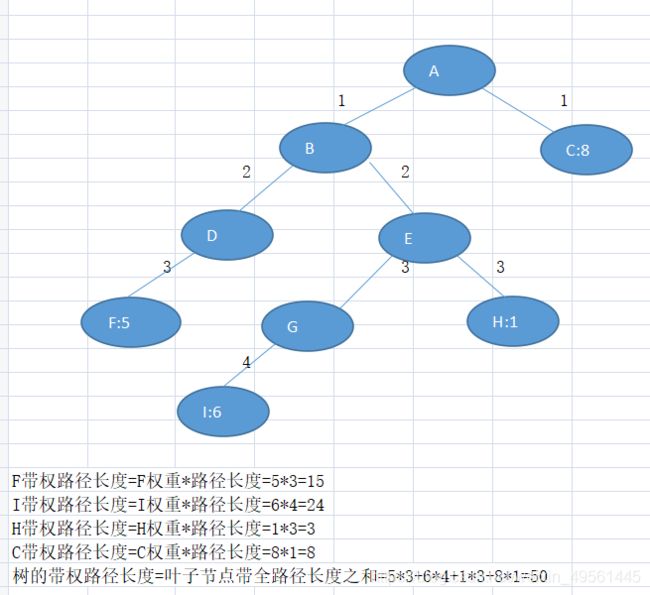
下图：根节点到F节点路径为：A ->B->D->F

路径长度

在一棵树中，从一个结点到另一个结点所经过的“边”的数量，被我们称为两个结点之间的路径长度;若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1;下图中
从根结点A到叶子结点F，共经过了3条边，因此路径长度是3

结点的带权路径长度

结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积

树的带权路径长度

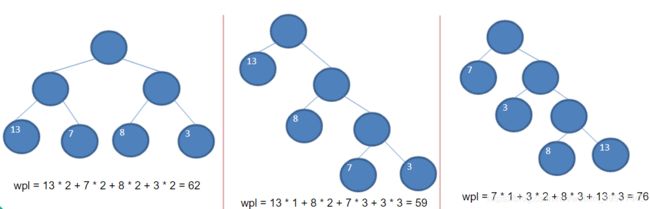
树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
上图树的带全路径长度则为50。

WPL最小的就是赫夫曼树

如：上图的第二个树WPL最小即为赫夫曼树

赫夫曼树创建

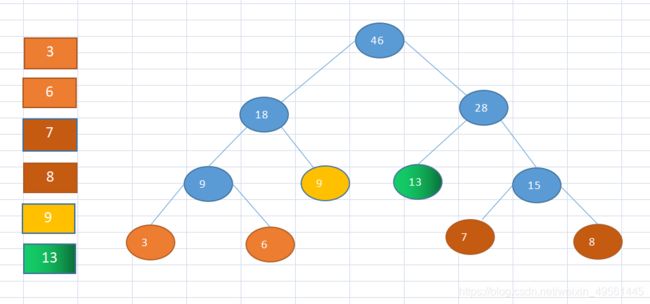
创建赫夫曼树的步骤：

• 1 从小到大进行排序, 将每一个数据，每个数据都是一个节点，每个节点可以看成是一颗最简单的二叉树

• 2 取出根节点权值最小的两颗二叉树

• 3 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和

• 4 再将这颗新的二叉树，将该根节点的权值大小与剩下的数据进行比较即再次排序，不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树

使用代码构建

public  static void createHuffmanTree(int[] arr){

        //需要比较大小，且需要重复比较大小优先使用优先级队列
        var  priorityQueue=new PriorityQueue<Node>(Comparator.comparingInt(e->e.value));
        for (int i : arr) {
            priorityQueue.add(new Node(i));
        }

        while (priorityQueue.size()>1){

            Node nodeLeft = priorityQueue.poll();
            Node nodeRight=priorityQueue.poll();
            if (nodeLeft!=null&&nodeRight != null){

                Node parentNode=new Node(nodeLeft.value+nodeRight.value);
                parentNode.left=nodeLeft;
                parentNode.right=nodeRight;
                priorityQueue.remove(nodeLeft);
                priorityQueue.remove(nodeRight);
                priorityQueue.add(parentNode);
            }
        }
        Node root = priorityQueue.poll();

        TreeOperation<Node> tree = new TreeOperation<>();
        tree.show(root);
    }

构建结果与上图所画完全一致

赫夫曼树的应用场景

apache负载均衡的按权重请求策略的底层算法、 生活中的路由器的路由算法、利用哈夫曼树实现汉字点阵字形的压缩存储

赫夫曼编码

基本介绍

赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式, 属于一种程序算法

赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间

赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，称之为最佳编码

背景

赫夫曼编码出现以前

通信领域中信息的处理方式

1 定长编码

比如 一段文字“BADCADFEED”，显然用二进制数字（0和1）表示是很自然的想法。

传输的数据就是“001000011010000011101100100011”，对方接收时同样按照3位一组解码。如果一篇文章很长，这样的二进制串也非常的可怕。而且事实上，每个字母或者汉子的出现频率是不同的。

2 变长编码

比如 “I want to get more money” 总共24个字符(包含空格)

各个字符对应的个数：
a:1 r:1 y:1 w:1 I:1 g:1 m:2 n:2 e:3 o:3 t:3 空格：5

对应二进制为：

按照各个字符出现的次数进行编码，原则是出现次数越多的，则编码越小，比如 空格出现了5次， 编码为0 ,其它依次类推.
0= , 1=e 10=o, 11=t, 100=m, 101=n, 110=a, 111=r, 1000=y, 1001=w, 1010=I ，1011=g

按以上规则则在传输"I want to get more money" 字符串时则对应编码为：
10100100111010111…

字符的编码都不能是其他字符编码的前缀，符合此要求的编码叫做前缀编码， 即不能匹配到重复的编码.很明显变长编码不是前缀编码,会造成匹配的多义性；所以就有了赫夫曼编码

编码

var string=“I want to get more money”; --以此字符串说明

1 统计各个字符出现的次数

a:1 r:1 y:1 w:1 I:1 g:1 m:2 n:2 e:3 o:3 t:3 空格：5

对应的byte： 97:1 114:1 121:1 119:1 73:1 103:1 109:2 110:2 101:3 111:3 116:3 32:5

private static HashMap<Byte, Integer> getByteCount(byte[] byteArray){

         var map=new HashMap<Byte, Integer>();
         for (var cb : byteArray) {

             //map.merge(cb, 1, (k, v)->(map.get(cb)+1));

            map.compute(cb, (k,v)->map.getOrDefault(cb, 0)+1);
        }
        
        return map;
    }

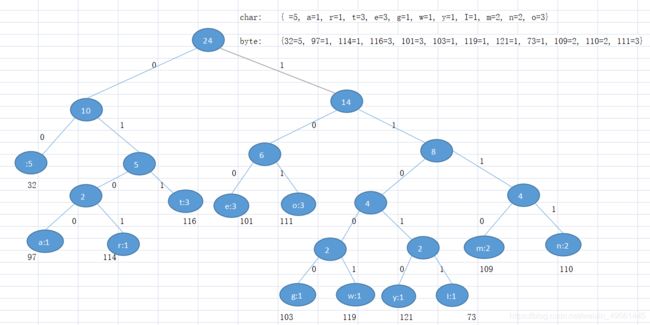
2 按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值

private static TreeNode<Byte>  createHuffmanTree(byte[] byteArray,List<TreeNode<Byte>> list){

        var map= getByteCount(byteArray);//统计的字符将作为赫夫曼树的叶子节点

        var  priorityQueue=new PriorityQueue<TreeNode<Byte>>(Comparator.comparingInt(e->e.value));

        map.forEach((k,v)-> {

            TreeNode<Byte> characterTreeNode = new TreeNode<>(k, v);

            priorityQueue.add(characterTreeNode);
            list.add(characterTreeNode);

        });

       while (priorityQueue.size() >1){

           var nodeLeft = priorityQueue.poll();
           var nodeRight = priorityQueue.poll();
           if (nodeLeft!=null&&nodeRight != null){

               var nodeParent=new TreeNode<Byte>(null,nodeLeft.value+nodeRight.value);
               nodeParent.left=nodeLeft;
               nodeParent.right=nodeRight;

               nodeLeft.parent=nodeParent;
               nodeRight.parent=nodeParent;
               priorityQueue.remove(nodeRight);
               priorityQueue.remove(nodeLeft);

               priorityQueue.add(nodeParent);
           }
       }

        return priorityQueue.poll();
    }

3 根据赫夫曼树，给各个字符规定编码，向左的路径为0，向右的路径为1 ，各个字符最终作为赫夫曼树的叶子节点

每个字符的路径：

：00 a:0100 r:0101 t:011 e:100 o:101 g:11000 w:11001 y:11010 I:11011 m:1110 n:1111

private static void getTreePathCodeStatus(List<TreeNode<Byte>> list) {


        var build=new StringBuilder();

        list.forEach(node -> {

            var currentNode=node;
            while (currentNode.parent!=null){//由于字符位于叶子节点则直接向上找父节点即可得出路径
                build.insert(0, currentNode.parent.left== currentNode ?'0':'1');
                currentNode = currentNode.parent;
            }

            if (node.key!=null){
                ENCODE_MAP.put(node.key, build.toString());
                build.delete(0, build.length());
            }
        });
 
    }

4 按照上面的赫夫曼编码， 对应字符串对应的编码(补码)为 (赫夫曼是无损压缩)

11011001100101001111011000111010011000100011001110101010110000111010111110011010
此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性

注意

• 此编码串是以补码的形式存在
• 这个赫夫曼树根据排序方法(有相同权值的时候)不同，也可能不太一样，这样对应的赫夫曼编码也不完全一样，但是树的带权路径长度(wpl)是一样的，都是最小的。
• 实际开发中均已byte字节进行编码压缩

public static  byte[] huffmanEnCode(byte[] byteArray,String name,String parentDirName,boolean isCreateFile){

            Objects.requireNonNull(byteArray);

            if (byteArray.length==0){
                System.out.println("The file is empty!");
                return null;
            }

            var list = new ArrayList<TreeNode<Byte>>();
            //生成赫夫曼树
            var root= createHuffmanTree(byteArray,list);


            //显示赫夫曼树
            if(byteArray.length<30){
                new TreeOperation<TreeNode<Byte>>().show(root);
            }

            //获取赫夫曼路径二进制字符串
           getTreePathCodeStatus(list);

         return encode(byteArray,name,parentDirName,isCreateFile);

    }

解码

赫夫曼解码是对编码的进行反编译过程，即还原过程

1 首先我们需要获取解码表，编码表一般会在编码的时候写入压缩文件中，所以我们需要读取文件获取编码表，更据编码表构建解码表

public  static  byte[] huffmanDecode(byte[] encodedArr,HashMap<Byte,String> encodedMap){


        StringBuilder encodedStr= new StringBuilder();

        //将字节数组转成二进制字符编码串
        for (var i = 0; i < encodedArr.length; i++) {

            encodedStr.append(decodeBytesToInt(encodedArr[i],i==encodedArr.length-1));
        }


        //获取解码表
        var decodedMap=new HashMap<String,Byte>();//解码表

        encodedMap.forEach((Key,Value)-> decodedMap.put(Value,Key));
        encodedMap.clear();

        return  decode(decodedMap, encodedStr);
    }

2 读取文件中的字节数组解析成编码串，即对应1101100…此种形式的赫夫曼树路径编码串

解析关键函数

 private static String decodeBytesToInt( byte bytes,boolean isLast) {

        var s=Integer.toBinaryString(Byte.toUnsignedInt(bytes));//toUnsignedInt转成无符号位整型，如果是负数二进制则为8位，如果是正数或者0，会存在高位丢失不满足8位的情况

        if (isLast&&s.length() <=lastLength){//最后一位如果是正数或者本身就是0则需要和压缩前时的最后一位长度比较。
            // 假如压缩前最后位为00111，现在转成二进制高位的0都被省略后是111。长度差2，这种需要补2个0，
            // 假如压缩前最后位为111，现在转成二进制后也是111。长度相等,这种无需补0
            //处理最后一个字节是正数或者是0，可能不足8位。因为其在压缩的时候长度就不够8位,但是在使用补码的时候原来前面的0会被忽略掉，所以要补齐
            return  "0".repeat(lastLength-s.length())+s;
        }
        //负数底层是32位，无符号处理后肯定长度为8,则不会拼接，如果是正数或者0经过toBinarySting处理高位会丢失导致不满足8位的情况则需要拼接
        return  "0".repeat(8-s.length())+s;

    }

3 从第二步骤的编码串从解码表里进行匹配解析

private  static byte[] decode(HashMap<String,Byte> decodedMap, StringBuilder encodedBuilder){

        int startIndex=0;

        var list= new ArrayList<Byte>();

        for (var i = 1; i < encodedBuilder.length()+1; i++) {
            String str;

            if (decodedMap.containsKey(str=encodedBuilder.substring(startIndex, i))){

                list.add(decodedMap.get(str));
                startIndex=i ;

            }
        }

        //解压后的字节数组
        var bytes =new byte[list.size()];
        for (var i = 0; i < bytes.length; i++) {
            bytes[i]=list.get(i);
        }

        list.clear();
        decodedMap.clear();

        System.out.println("解压成功");

        return  bytes;
    }

• 赫夫曼压缩注意事项：

• 1 如果文件本身就是经过压缩处理的，那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件 [举例压一个 .ppt]

• 2 赫夫曼编码是按字节来处理的，因此可以处理所有的文件(二进制文件、文本文件) [举例压一个.xml文件]

• 3 如果一个文件中的内容，重复的数据不多，压缩效果也不会很明显.

完整代码

使用赫夫曼树对文件进行压缩及解压