机器学习实战-PCA主成分分析、降维

降维技术

很多时候，原始数据是多维度的，在计算的时候会带来很大的资源开销。而且数据本身有很多的冗余，我们可以去除一些不必要的特征，使得数据简化，降低算法的计算开销。因此需要利用降维技术来实现。

PCA(Principal Component Analysis)主成分分析

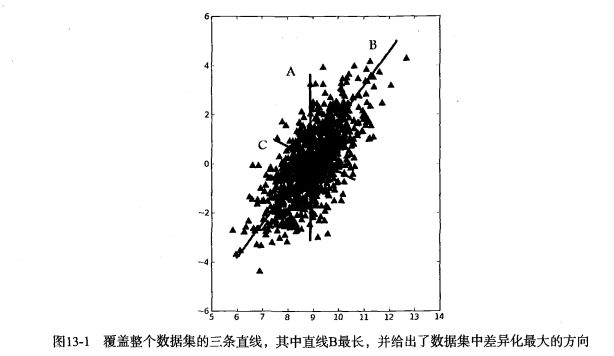
在PCA中，数据从原来的坐标系转化到新的坐标系中。当然这里新的坐标系也不是随便设定的，而是应该根据数据本身的特征来设计。通常第一个新坐标轴选择的是原始数据方差最大的方向，第二个坐标轴是与第一个坐标轴正交且具有最大方差的方向。这句话的意思就是，第二个选取的方向应该和第一个方向具有很弱的相关性。如果有很强的相关性的话，那么选其中一个就ok了。然后依此类推，选出后面的方向，其数目应该和原始数据的特征数目一致。
通常我们会发现，大部分的方差就集中在前面几个方向中，因此可以忽略后面的方向，达到降维的效果。
然后书上有这么一段话，介绍实现该过程的伪代码。

看不懂这里的协方差矩阵是啥，为什么是这样子的？
只好从初中数学的方差开始学习了。。。

基本统计学概念

统计学里有几个基本的概念，有均值，方差，标准差等等。比如有一个含有n个样本的集合： X={x1,...,xn}
那么，
均值： X¯¯¯=∑ni=1xin
标准差： s=∑ni=1(xi−X¯¯)2n−1−−−−−−−−−−√
方差： s2=∑ni=1(xi−X¯¯)2n−1
根据以前我们所知道的，方差呢是用来衡量数据的波动程度的，如果大部分数据都在均值附近，那么方差就会是很小的值。

协方差是什么

分析完了方差我们再看看啥是协方差。
方差描述的是其本身数据的情况，如果我们想知道，某2种数据之间的关系，该怎么描述呢，比如，男生帅气程度(or猥琐程度)，和受女孩子欢迎程度。假设这里有样本集合 f(x,y)=(xi,...,yi) ，x表示男生帅气指数，y表示相应的受女生欢迎指数，那么2者之间的关联程度可以这么定义：

cov(X,Y)=∑ni=1(Xi−X¯¯¯)(Yi−Y¯¯¯)n−1

那么从上面可知，如果结果为正值，那么说明2者是正相关，男生越帅，女生越喜欢。。(废话-.-)

协方差矩阵是什么

再看看协方差矩阵，上面提到的协方差是二维数据的情况，那么如果是多维，比如三维，x,y,z.那么两两之间的协方差就有6个，再加上自己与自己的协方差就有9个，可以画成矩阵的形式了。
C=⎛⎝⎜cov(x,x)cov(y,x)cov(z,x)cov(x,y)cov(y,y)cov(z,y)cov(y,z)cov(y,z)cov(z,z)⎞⎠⎟

PCA与协方差矩阵

讲完协方差矩阵，再回头看看PCA，PCA和这个矩阵又有啥关系呢。
PCA的理念就是将高维空间的数据映射到低维空间，降低维度之间的相关性，并且使自身维度的方差尽可能的大。那么哪种数据方式可以同时表达维度之间的相关性以及，维度本身的方差呢？就是上面提到的协方差矩阵。协方差矩阵对角线上是维度的方差，其他元素是两两维度之间的协方差(即相关性)。
PCA的目的之一：降低维度之间的相关性，也就说减小协方差矩阵非对角线上的值。如何减小呢？可以使协方差矩阵变成对角矩阵。对角化后的矩阵，其对角线上是协方差矩阵的特征值。这里又提到了特征值，看看它到底有啥潜在的含义。

特征值与特征向量

根据其定义Ax=cx,其中A是矩阵，c是特征值，x是特征向量；
Ax矩阵相乘的含义就是，矩阵A对向量x进行一系列的变换(旋转或者拉伸)，其效果等于一个常数c乘以向量x。
通常我们求特征值和特征向量是想知道，矩阵能使哪些向量(当然是特征向量)只发生拉伸，其拉伸程度如何(特征值的大小)。这个真正的意义在于，是为了让我们看清矩阵能在哪个方向(特征向量)产生最大的变化效果。

好比以下来自书本的图片：

回头再看刚才的协方差矩阵对角化之后，得到了协方差矩阵的特征值；那么我们就能明白协方差矩阵在特征值对应的特征向量的方向上有最大的变化效果。当然这里的特征值会有多个，我们只需要取最大的几个就可以了，特征值越大，表示其在特征向量上的变化越大。我们把这几个特征值对应的特征向量的方向作为新的维度，于是，降维的目的达到了。。。
现在，再看看最上面来自书本的截图，就明白为什么要求协方差矩阵，然后又是特征值。。。

code

from numpy import *

def loadDataSet(fileName,delim='\t'):
    fr=open(fileName)
    stringArr=[line.strip().split(delim) for line in fr.readlines()]
    datArr=[map(float,line) for line in stringArr]
    return mat(datArr)

def pca(dataMat,topNfeat=9999999):
    #原始数据归一化
    meanVals=mean(dataMat,axis=0)
    meanRemoved=dataMat-meanVals
    #求协方差矩阵，python真方便，一大坨计算，一个函数搞定
    covMat=cov(meanRemoved,rowvar=0)
    #求特征值，特征向量
    eigVals,eigVects=linalg.eig(mat(covMat))
    #特征值排序
    eigValInd=argsort(eigVals)
    eigValInd=eigValInd[:-(topNfeat+1):-1]
    redEigVects=eigVects[:,eigValInd]
    #原始数据映射到新的维度空间
    lowDataMat=meanRemoved*redEigVects
    reconMat=(lowDataMat*redEigVects.T)+meanVals
    return lowDataMat,reconMat

end

参考：
线性代数应该这样学
http://www.zhihu.com/question/20507061/answer/16610148
协方差矩阵与PCA.pdf