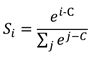神经网络15分钟入门——使用python从零开始写一个两层神经网络

本篇是该系列的第三篇，建议在阅读本篇文章之前先看前两篇文章。

神经网络15分钟入门！足够通俗易懂了吧

神经网络15分钟入门！——反向传播到底是怎么传播的？

在本文中将使用python实现之前描述的两层神经网络，并完成所提出的“象限分类”的问题。

需要注意的是，虽然标题叫做神经网络15分钟入门，但是到这篇文章，对于没接触过python的同学，15分钟怕是不太够。好在python本身不算太难，如果你有其他语言的基础，结合本文尽量详细的讲解，对于算法层面的理解应该还是可以做到的。如果还是不能理解，建议先入门python再来看本文，毕竟想做深度学习，对语言的掌握是基本要求。

另外，这篇文章的正确食用方法是将代码搞到自己的电脑上，然后单步调试逐行看参数的变化，如有不明白的地方再对照文章中的讲解来理解。单纯靠看文章是不太容易融会贯通的（可以脑内debug的同学可以忽略）。

一、运行环境

运行环境：Python 3.6.5+Anaconda3+VS Code

Anaconda是一个环境管理器，安装Anaconda，就相当于安装了python+各种工具包，这些工具包在我们进行神经网络的应用时十分必要。

VS Code是微软的免费代码编辑器，功能相当强大，插件相当丰富，界面非常美观。当然，你也可以用pycharm或者eclipse，看个人习惯。

运行环境的搭建就不详细介绍了，在网上能找到很多教程，如果有疑问可以留言，需要的话我会写一篇番外对环境搭建进行详细讲述。

二、编程实现

1.导入numpy包

import numpy as np  
#numpy是一个强大的数学工具包
#我们后边要用到的是numpy中的数组类型、矩阵运算等
#不明白没关系，用到的时候会再解释

2.前向传播函数

# 前向传播函数
# - x：包含输入数据的numpy数组，形状为（N，d_1，...，d_k）
# - w：形状为（D，M）的一系列权重
# - b：偏置，形状为（M，）
def affine_forward(x, w, b):   
    out = None                       # 初始化返回值为None
    N = x.shape[0]                   # 重置输入参数X的形状
    x_row = x.reshape(N, -1)         # (N,D)
    out = np.dot(x_row, w) + b       # (N,M)
    cache = (x, w, b)                # 缓存值，反向传播时使用
 return out,cache           

这一段程序是定义了了一个名为affine_forward的函数，其功能就是计算这个公式（仿射）：

如果不记得这个公式了就回去看一下第一篇文章

这个函数的输入参数就是公式中的矩阵X，W1和b1，对应到程序中就是x，w和b。

不过需要注意的是，程序中的输入参数x，其形状可以是（N，d_1，...，d_k），这是什么意思呢？在我们这个例子中，输入参数x是：

[2,1],  
[-1,1],  
[-1,-1],  
[1,-1]]

它是一个4行2列的二维数组，那么x的形状就是(4,2)，对应的参数N=4，d_1=2。这是我们用来做训练的坐标数据，分别对应了I、II、III、IV象限。

在某些应用场景中，x的维度可能更高。比如对于一个20*20像素的4张灰度图，x的形状将是(4,20,20)，对应的参数就是N=4，d_1=20，d_2=20。（这里边第一个参数用N表示，它代表的是同时用于计算前向传播的数据有几组，后边的参数d_1~d_k代表的是数据本身的形状。）

对于这种维度大于2的x来说，需要对其进行重新塑形，也就是将(4,20,20)的高维数组变化为(4,20*20)这样的二位数组。

为什么要这么做呢？是为了方便计算。这样变换之后高维的向量被“拍扁”成一维向量（长度为20*20的一维向量），对应的W和b也都是一维的，既统一了参数形式，又不会影响数据的正常使用。

这个“拍扁”的动作，是用上述代码中的这两行完成的：

N = x.shape[0]                 # 重置输入参数X的形状     
x_row = x.reshape(N,-1)        # (N,D)

x.shape[0]是获取数组x的第0维长度，也就是数据的组数，对于上述的4行2列的数组，其值为4；对于上述(4,20,20)的数组，其值也为4.

x.reshape(N,-1)是对x重新塑形，即保留第0维，其他维度排列成1维。对于形状为(4,2)的数组，其形状不变，对于形状为(4,20,20)的数组，形状变为（4,20*20）。以此类推。

在完成reshape后，就可以进行矩阵的线性运算了：

out = np.dot(x_row, w)+ b       # (N,M)

.dot就是numpy中的函数，可以实现x_row与w的矩阵相乘。x_row的形状为(N,D)，w的形状为(D,M)，得到的out的形状是(N,M)。

cache =(x, w, b)   # 缓存值，反向传播时使用

上面这句是将当前x，w和b的值缓存下来，留作反向传播时使用。

3.反向传播函数

# 反向传播函数
# - x：包含输入数据的numpy数组，形状为（N，d_1，...，d_k）
# - w：形状（D，M）的一系列权重
# - b：偏置，形状为（M，）
def affine_backward(dout, cache):   
    x, w, b = cache                              # 读取缓存
    dx, dw, db = None, None, None                # 返回值初始化
    dx = np.dot(dout, w.T)                       # (N,D)    
    dx = np.reshape(dx, x.shape)                 # (N,d1,...,d_k)   
    x_row = x.reshape(x.shape[0], -1)            # (N,D)    
    dw = np.dot(x_row.T, dout)                   # (D,M)    
    db = np.sum(dout, axis=0, keepdims=True)     # (1,M)    
 return dx, dw, db

这一段是实现计算仿射层的反向传播的函数。这篇文章的2.3节讲的就是这段代码的原理，如果不清楚可以先出门左转看一下。

函数中第一句就是读取缓存的x，w和b的值，为什么要这样做呢？仿射变换反向传播的最重要的3个目的，分别是：①更新参数w的值②计算流向下一个节点的数值③更新参数b的值。“更新”的时候需要“旧”值，也就是缓存值，具体操作如下：

①为了得到w的值，要将上一节点输入的值（dout）乘以x。

dw = np.dot(x_row.T, dout)         # (D,M) 

②为了得到流入下一个节点的值（x），要将上一节点的输入值（dout）乘以w。你可能发现了，①中为了得到w是乘以的x，②中为了得到x是乘以的w，也就是将系数交叉相乘了。

 dx = np.dot(dout, w.T)            # (N,D)    

③为了得到b，只需要将out直接传过来就可以，为了保持维度一致，这里将out求和。

db = np.sum(dout, axis=0, keepdims=True)    # (1,M) 

在仿射变换反向传播这里，各种矩阵的维度可能会让你感到困惑。这里的维度包含三个，分别是D、M和N。

看一下下图，其中包括两个仿射变换，我们以第一个举例，其变换公式为H=X*W1+b1。该仿射变换对应到程序中的D的值为2，M的值为50，N的值为4。怎么理解呢？X的维度就是N*D，而M的值就是W1的第二个维度，这里记住就好了，每个仿射变换都是这样的（其实不记住也没关系，这里没有什么物理含义，就是单纯的矩阵变换的维度而已。这几个维度在反向传播时可能难理解，这是数学公式推导来的，迷惑的时候找出这篇文章过来看一遍就明白了）。

注意看矩阵维度

4.参数初始化

X = np.array([[2,1],  
            [-1,1],  
            [-1,-1],  
            [1,-1]])      # 用于训练的坐标，对应的是I、II、III、IV象限
t = np.array([0,1,2,3])   # 标签，对应的是I、II、III、IV象限
np.random.seed(1)         # 有这行语句，你们生成的随机数就和我一样了

# 一些初始化参数  
input_dim = X.shape[1]     # 输入参数的维度，此处为2，即每个坐标用两个数表示
num_classes = t.shape[0]   # 输出参数的维度，此处为4，即最终分为四个象限
hidden_dim = 50            # 隐藏层维度，为可调参数
reg = 0.001                # 正则化强度，为可调参数
epsilon = 0.001            # 梯度下降的学习率，为可调参数
# 初始化W1，W2，b1，b2
W1 = np.random.randn(input_dim, hidden_dim)     # (2,50)
W2 = np.random.randn(hidden_dim, num_classes)   # (50,4)
b1 = np.zeros((1, hidden_dim))                  # (1,50)
b2 = np.zeros((1, num_classes))                 # (1,4)

这一段程序对一些必要的参数进行了初始化，程序较为简单，看注释即可，不再详细解释。

对于训练数据以及训练模型已经确定的网络来说，为了得到更好的训练效果需要调节的参数就是上述的隐藏层维度、正则化强度和梯度下降的学习率，以及下一节中的训练循环次数。

5.训练与迭代

for j in range(10000):   #这里设置了训练的循环次数为10000
 # ①前向传播
    H,fc_cache = affine_forward(X,W1,b1)                 # 第一层前向传播
    H = np.maximum(0, H)                                 # 激活
    relu_cache = H                                       # 缓存第一层激活后的结果
    Y,cachey = affine_forward(H,W2,b2)                   # 第二层前向传播        
 # ②Softmax层计算
    probs = np.exp(Y - np.max(Y, axis=1, keepdims=True))    
    probs /= np.sum(probs, axis=1, keepdims=True)        # Softmax算法实现
 # ③计算loss值
    N = Y.shape[0]                                       # 值为4
    print(probs[np.arange(N), t])                        # 打印各个数据的正确解标签对应的神经网络的输出
    loss = -np.sum(np.log(probs[np.arange(N), t])) / N   # 计算loss
    print(loss)                                          # 打印loss
 # ④反向传播
    dx = probs.copy()                                    # 以Softmax输出结果作为反向输出的起点
    dx[np.arange(N), t] -= 1                             # 
    dx /= N                                              # 到这里是反向传播到softmax前
    dh1, dW2, db2 = affine_backward(dx, cachey)          # 反向传播至第二层前
    dh1[relu_cache <= 0] = 0                             # 反向传播至激活层前
    dX, dW1, db1 = affine_backward(dh1, fc_cache)        # 反向传播至第一层前
# ⑤参数更新
    dW2 += reg * W2
    dW1 += reg * W1
    W2 += -epsilon * dW2
    b2 += -epsilon * db2
    W1 += -epsilon * dW1
    b1 += -epsilon * db1

这段程序是网络训练的核心，我将按照①前向传播②Softmax层③计算loss值④反向传播⑤参数更新这五个小结的顺序依次讲解：

①前向传播

 # ①前向传播
    H,fc_cache = affine_forward(X,W1,b1)                 # 第一层前向传播
    H = np.maximum(0, H)                                 # 激活
    relu_cache = H                                       # 缓存第一层激活后的结果
    Y,cachey = affine_forward(H,W2,b2)                   # 第二层前向传播   

第一句H,fc_cache = affine_forward(X,W1,b1) 调用了之前写的前向传播的函数，完成了第一层网络的矩阵线性代数运算。

第二句H = np.maximum(0, H)是从0和H中选择较大的值赋给H，也就是实现了ReLU激活层函数。

第四句Y,cachey = affine_forward(H,W2,b2)，完成了第二层网络的矩阵线性代数运算。

②Softmax层计算

 # ②Softmax层计算
    probs = np.exp(Y - np.max(Y, axis=1, keepdims=True))    
    probs /= np.sum(probs, axis=1, keepdims=True)        # Softmax算法实现

这两行是为了实现Softmax层的计算，在之前我们说过，Softmax的计算公式是：

不过在实际应用中会存在一个问题，比如i的值等于1000时，e^1000在计算机中会变成无穷大的inf，后续计算将无法完成，所以程序中会对计算公式做一些修改，实际使用的公式为：

在指数上减去常数C不影响最终结果（证明略），而这个常数C通常取i中的最大值。

第一句probs = np.exp(Y - np.max(Y, axis=1, keepdims=True)) 就是求输出各个行的指数值，举个例子，Y的值如果是：

[[-4,17,20,-4],
[10,-2,5,3],
[-5,3,4,10],
[-5,5,5,2]]

np.max(Y, axis=1, keepdims=True)计算得到的是[[20],[10],[10],[5]]，后边括号里的参数axis代表以竖轴为基准 ，在同行中取值； keepdims=True代表保持矩阵的二维特性。

所以np.exp(Y - np.max(Y, axis=1, keepdims=True)) 代表：Y矩阵中每个值减掉改行最大值后再取对数。

第二句probs /= np.sum(probs, axis=1, keepdims=True) 以行为单位求出各个数值对应的比例。也就是最终实现了Softmax层的输出。

③计算loss值

 # ③计算loss值
    N = Y.shape[0]                                       # 值为4
    print(probs[np.arange(N), t])                        # 打印各个数据的正确解标签对应的神经网络的输出
    loss = -np.sum(np.log(probs[np.arange(N), t])) / N   # 计算loss

复习一下：交叉熵损失的求法是求对数的负数。

第一句N = Y.shape[0]取了最终输出的维度，这个例子中为4，即四个象限。

第二句打印各个数据的正确解标签对应的神经网络的输出。

其中probs[np.arange(N), t]讲解一下：

N为4时，np.arange(N)会生成一个Numpy数组[0,1,2,3]。t中标签是以[0,1,2,3]的形式储存的，所以probs[np.arange(N), t]能抽出各个数据的正确解标签对应的神经网络输出，在这个例子中，probs[np.arange(N), t]会成成numpy数组[probs[0,0], probs[1,1], probs[2,2], probs[3,3]]。

第三句loss = -np.sum(np.log(probs[np.arange(N), t])) / N中先求了N维数据中的交叉熵损失，然后对这N个交叉熵损失求平均值，作为最终loss值。

④反向传播

 # ④反向传播
    dx = probs.copy()                                    # 以Softmax输出结果作为反向输出的起点
    dx[np.arange(N), t] -= 1                             # 
    dx /= N                                              # 到这里是反向传播到softmax前
    dh1, dW2, db2 = affine_backward(dx, cachey)          # 反向传播至第二层前
    dh1[relu_cache <= 0] = 0                             # 反向传播至激活层前
    dX, dW1, db1 = affine_backward(dh1, fc_cache)        # 反向传播至第一层前

反向传播计算是从Softmax层的输出开始的。你是不是想问为什么不是从loss值开始算？

回看上一篇文章的2.5节，你会发现Softmax-with-Loss层的反向传播结果计算，本身就是与loss无关的。而只与Softmax层输出结果和教师标签有关。换句话说，即使是从loss开始计算反向传播，经过一系列化简之后，这个loss值也会被化简掉，化简后的结果只包括Softmax层的输出和教师标签。

第一句代码很简单，就是将Softmax的输出值赋给dx， 这里dx代表反向传播的主线值。dx[np.arange(N), t]-=1这句代码

第二句代码是实现上一篇文章中y-t的操作（y就是Softmax层的输出）。dx[np.arange(N), t]-=1这句代码中，dx是一个4*4的数组，而t是一个内容为[0,1,2,3]的数组（见其初始化），N的值为4。np.arrange(N)会生成一个从0到3的数组[0,1,2,3]，因为t中的标签是以[0,1,2,3]的形式存储的，所以dx[np.arange(N), t]能抽出各个数据的正确解标签对应的神经网络的输出。在这个例子中dx[np.arange(N), t]会成成NumPy数组[dx[0,0],dx[1,1],dx[2,2],dx[3,3]。

第四、六句试一次仿射变幻的反向传播，上边说过了，不在具体解释了。

第五句是ReLU激活层的反向传播，至于为什么这样写，也去看上一篇文章吧~

⑤参数更新

# ⑤参数更新
    dW2 += reg * W2
    dW1 += reg * W1
    W2 += -epsilon * dW2
    b2 += -epsilon * db2
    W1 += -epsilon * dW1
    b1 += -epsilon * db1

前两行是引入正则化惩罚项更新dW，后四行是引入学习率更新W和b。这部分理解起来比较简单，如果有疑问可以参考上篇文章的第3节。

6.验证

test = np.array([[2,2],[-2,2],[-2,-2],[2,-2]])
H,fc_cache = affine_forward(test,W1,b1)               #仿射
H = np.maximum(0, H)                                  #激活
relu_cache = H
Y,cachey = affine_forward(H,W2,b2)  #仿射
 # Softmax
probs = np.exp(Y - np.max(Y, axis=1, keepdims=True))    
probs /= np.sum(probs, axis=1, keepdims=True)  # Softmax
print(probs)
for k in range(4):
    print(test[k,:],"所在的象限为",np.argmax(probs[k,:])+1)

给出了一组数据test，对已经训练好的网络进行验证。

其实验证的方法和训练时的正向传播的过程基本一致，即第一层网络线性计算→激活→第二层网络线性计算→Softmax→得到分类结果。

这部分代码在之前也大多讲过，不再详述。

三、运行结果

在运行10000次迭代后，loss值以肉眼可见的速度下降。

最终loss值为：0.0040015

最终输出结果为：

可见分类正确。

四、总结

本例是一个很简单的神经网络的例子，我们只用了一组数据用来训练，其训练结果应该是比较勉强的。之所以最终效果还行，只是我们选择验证的例子比较合适。要想得到比较完美的模型，需要有大量的、分散的训练数据，比如第一象限不仅要有[1,1]这种数据，还要有[1000,1]，[1,1000]这种，这里就不再详述了。

“神经网络15分钟入门”系列到这里就结束啦。如果这三篇文章里的内容能够融会贯通，相信对你后边学习深度学习会有一些帮助。在神经网络学习过程中能遇到的难点和坑我尽量都点出来了，如果还有什么疑问请留言给我吧，也许会出一篇番外集中回答。

如果要获取本文的完整代码，可以关注我的公众号“看海的城堡”，微信号为“khscience”，回复“神经网络”就能拿到啦，公众号里可能还会有更多有趣的东西分享。

欢迎持续关注我的专栏与信号处理有关的那些东东

参考：

《深度学习入门：基于Python的理论与实现》