字符串——KMP算法

概述

百度百科：

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) 。

思路讲解

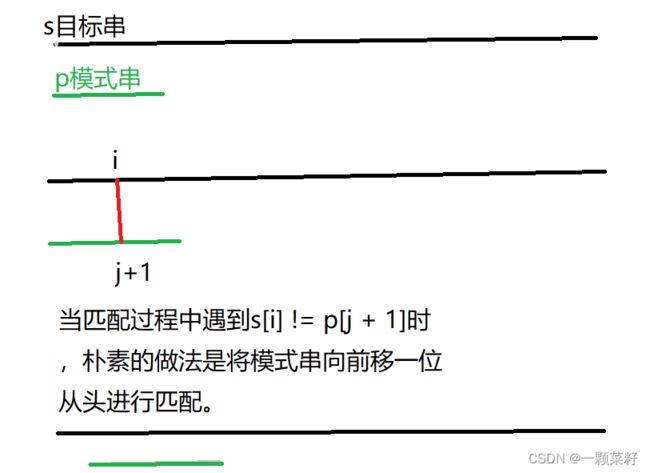
朴素解法

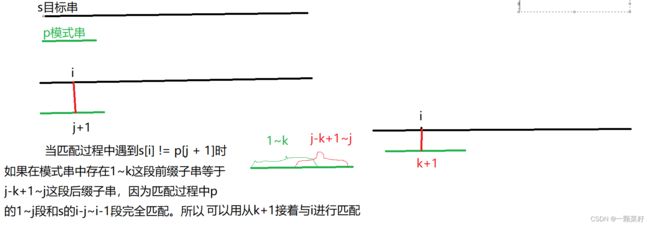
kmp优化

next数组

next[i] = j代表以i为终点的后缀与以1为起点的前缀相等的最长距离

构建方法：
1、初始化next[1]为0，因为长度为1的字符串没有前后缀
2、向前推进匹配，如果遇到不匹配的情况，就依据kmp的优化方式j = next[j]找到可以回退的近距离。继续匹配。

例题

给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤105
1≤M≤106
输入样例：
3
aba
5
ababa
输出样例：
0 2

N = 100010
M = 1000010

p = [0] * N
s = [0] * M
ne = [0] * N

n = int(input())
p[1 : n + 1] = list(input())
m = int(input())
s[1 : m + 1] = list(input())

##创建next数组
j = 0
for i in range(2, n + 1) :
	while j and p[i] != p[j + 1] : j = ne[j] # 其中条件中j是为了防止第一个不等的时候的死循环
	if p[i] == p[j + 1] : j += 1
	ne[i] = j

## 匹配
j = 0
for i in range(1 , m + 1) :
	while j and s[i] != p[j + 1] : j = ne[j]
	if s[i] == p[j + 1] : j += 1
	if j == n :
		print(i - n, end = " ")#因为返回的是索引所以不需要加1
		j = ne[j] ##当找到一个匹配状态后需要继续匹配

总结

kmp在匹配和创建next数组都是用的双指针，我们知道双指针可以来维护一段区间，而本题维护的是两端1~j, i - j + 1 ~ i的两段子串相等的区间，如果遇到不等的则通过之前保存的相等子串的信息来更新当前的区间。有点抽象了~~~