遗传算法求解TSP问题

摘要：

        采用遗传算法进行25个城市的TSP问题求解，通过遗传算法求解得出的最短路径值为29085.91，最优路径为24→15→25→20→19→6→8→17→3→13→7→5→11→1→2→14→4→9→12→21→10→16→22→18→23→24（数字为城市序号）。同时根据不同参数下的实验结果，得出结论，随着种群数量的增长及迭代次数的越来越多，遗传算法寻优的结果越来越好。当然，由于遗传算法本身具有一定的随机性，能否快速收敛得看具体参数设定。

1.1 遗传算法原理

        遗传算法是一种基于自然选择和群体遗传机理的搜索算法，它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象。

        在利用遗传算法求解问题时，问题的每一个可能解都被编码成一个“染色体”，即个体，若干个个体构成了群体(所有可能解)。在遗传算法开始时，总是随机的产生一些个体(即初始解)，根据预定的目标函数对每一个个体进行评估给出一个适应度值。基于此适应度值，选择一些个体用来产生下一代，选择操作体现了“适者生存"的原理，“好”的个体被用来产生下一代，“坏”的个体则被淘汰，然后选择出来的个体经过交叉和变异算子进行再组合生成新的一代，这一代的个体由于继承了上一代的一些优良性状，因而在性能上要优于上一代，这样逐步朝着最优解的方向进化。

        因此，遗传算法可以看成是一个由可行解组成的群体初步进化的过程。

1.2 实验步骤

        步骤一：设置 TSP 问题中25个城市的坐标值，限制每个城市只能拜访一次，并且回到出发的城市。本实验中25个城市坐标如下：

[1549,3408;  1561,2641;  3904,3453;  2216,1177;  1563,4906;

 3554,827;   2578,4370;  3358,2054;  143,4789;   610,774;

 1557,4064;  771,1823;   4753,4192;  2037,1897;  4692,1887;

 839,415;    4314,2696;  428,3626;   2725,543;   2349,263;

 770,2550;   1627,1361;  2139,3908;  1977,2775;  4345,11];

        步骤二：设置种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1；

        步骤三：初始化种群，计算每个个体的适应度值（即路径长短），执行交叉、变异、选择操作，生成新的种群；

        步骤四：判断终止条件（如果满足，则迭代结束。输出最终最短路径值以及绘制最优路径图；否则继续迭代优化，并实时更新最短路径值以及最优路径图）。

源代码如下：

%% 采用遗传算法进行TSP问题求解
%% 清理参数及原始变量
clear al1;
close all;
clc;
%% 设置25个城市坐标
C=[1549,3408;1561,2641;3904,3453;2216,1177;1563,4906;
   3554,827;2578,4370;3358,2054;143,4789;610,774;
   1557,4064;771,1823;4753,4192;2037,1897;4692,1887;
   839,415;4314,2696;428,3626;2725,543;2349,263;
   770,2550;1627,1361;2139,3908;1977,2775;4345,11];
 
 %% 设置参数
 P=100;           % 种群容量
 N=size(C,1);     % 城市个数
 maxIter=1000;    % 最大迭代次数
 Pm=0.1;          % 变异概率
%% 开始寻优
 % 初始种群
 Chro=[];
 for i=1:P
     temp=randperm(N);
     Chro=[Chro;temp];
 end
 % 计算种群中每个染色的适应度
 fit=fitness(Chro,C);
 for iter=1:maxIter
    % 交叉
    for i=1:P/2
        chro1=Chro(i,:);                           % 交叉配对中的第1个染色体
        chro2=Chro(i+P/2,:);                       % 交叉配对中的第2个染色体
        pos=randi(N-2)+1;                          % 随机选取交叉位置
        new_chro1=[chro1(1:pos) chro2(pos+1:end)]; % 新的染色体
        new_chro2=[chro2(1:pos) chro1(pos+1:end)]; % 新的染色体
        chro1_handled=handle(new_chro1);
        chro2_handled=handle(new_chro2);
        Chro(i,:)=chro1_handled;
        Chro(i+P/2,:)=chro2_handled;
    end
    % 变异
    for i=1:P
        if rand()0
                chro(i)=0;
            end
        end
        idx=find(chro==0);            % 找到删掉的基因所在的位置
        for i=1:length(idx)           % 逐个替换位未使用的基因
            chro(idx(i))=unused(i);
        end
    end
    chro_handled=chro;                % 返回值为处理后的染色体
 end
 %% 计算适应度，即路径的长度
 function fit=fitness(Chro,C)
    for i=1:size(Chro,1)
        possible_sol=Chro(i,:);                       % 拿到1个染色体
        possible_sol=[possible_sol possible_sol(1)];  % 将第一个城市坐标补充到末尾
        dist=0;                                       % 用于计算总距离
        for j=1:length(possible_sol)-1                    
            city1=possible_sol(j);                    % 第j个城市的编号
            city2=possible_sol(j+1);                  % 第j+1个城市的编号
            city1_C=C(city1,:);                       % 第j个城市的坐标
            city2_C=C(city2,:);                       % 第j+1个城市的坐标
            dist=dist+norm(city1_C-city2_C);          % 第j个城市和第j+1个城市的距离
        end
        fit(i)=dist;
    end
 end

1.3 实验结果

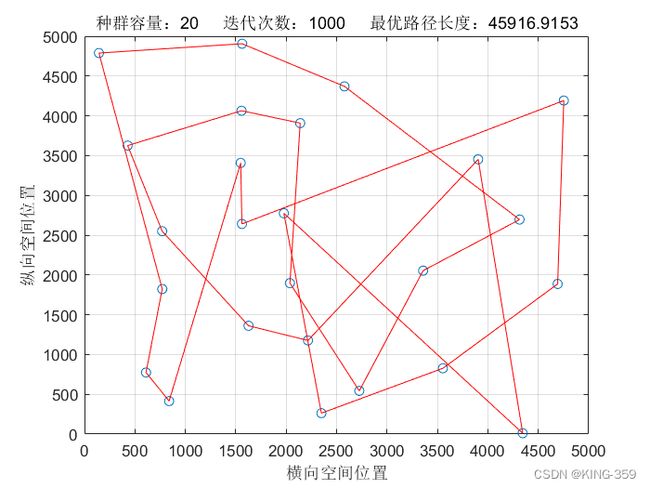
        种群数量 P=20，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.1

        种群数量 P=40，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.2

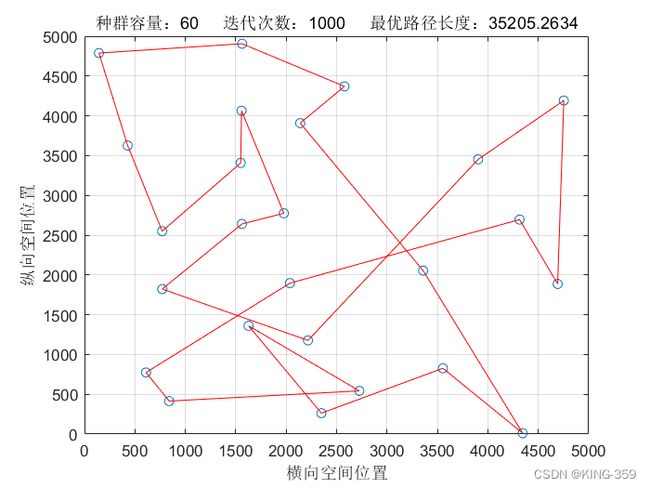
        种群数量 P=60，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.3

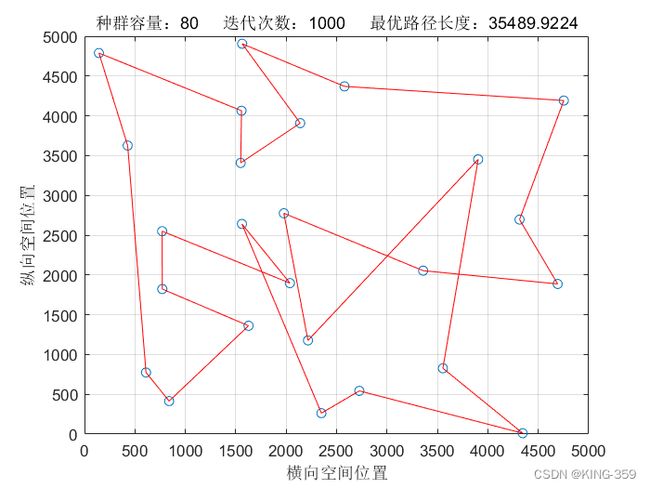
        种群数量 P=80，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.4

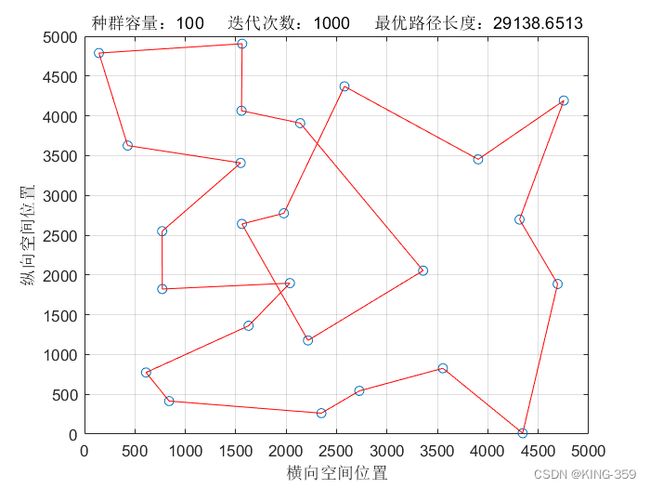
        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.5

        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=200，变异概率 Pm=0.1时，实验结果如下图所示：

图1.6

        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=400，变异概率 Pm=0.1时，实验结果如下图所示：

图1.7

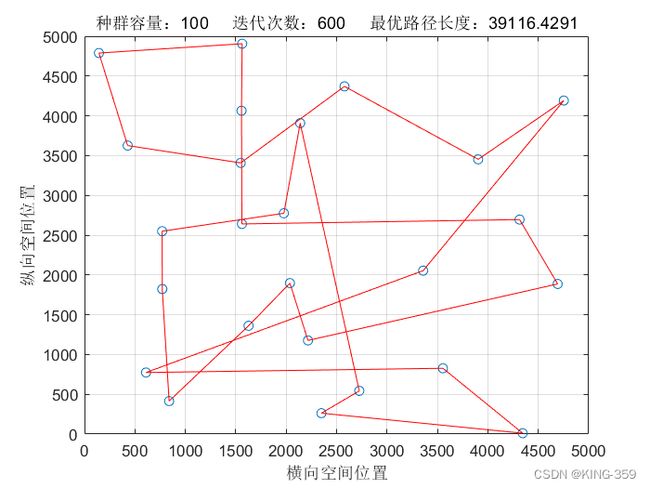
        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=600，变异概率 Pm=0.1时，实验结果如下图所示：

图1.8

        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=800，变异概率 Pm=0.1时，实验结果如下图所示：

图1.9

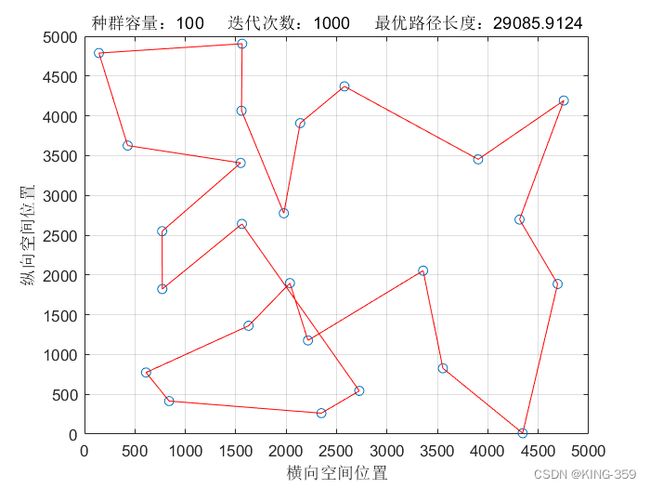
        种群数量 P=100，染色体基因数 N=25，迭代次数 maxIter=1000，变异概率 Pm=0.1时，实验结果如下图所示：

图1.10

1.4 不同参数下的结果与分析

种群数量P	染色体基因数N	迭代次数maxIter	变异概率Pm	最终结果
20	25	1000	0.1	45916.92
40	25	1000	0.1	39688.31
60	25	1000	0.1	35205.26
80	25	1000	0.1	35489.92
100	25	1000	0.1	29138.65
100	25	200	0.1	42388.17
100	25	400	0.1	41718.27
100	25	600	0.1	39116.43
100	25	800	0.1	35108.83
100	25	1000	0.1	29085.91

表1

        从表1中不同参数下得到的结果可以看出：针对25个城市的TSP问题，遗传算法求解得出的最短路径值为29085.91，最优路径为24→15→25→20→19→6→8→17→3→13→7→5→11→1→2→14→4→9→12→21→10→16→22→18→23→24（数字为城市序号）。

        同时，观察不同参数下得到的结果可以发现，随着种群数量的增长，遗传算法寻优的结果也越来越好；随着迭代次数的越来越多，遗传算法寻优的结果越来越好。当然，由于遗传算法本身具有一定的随机性，能否快速收敛得看具体参数设定。有时候随着种群数量和迭代次数增加，遗传算法寻优的结果可能还不如之前得到结果。