打印一棵二叉树(详细版)
打印一棵二叉树
二叉树:是一种重要的树状数据结构,通常由根节点,左子树和有子树构成,其中除叶子节点以外,每一个节点最少含有一个分支节点,最多含有两个分支节点。正是由于这种特殊的性质,使得二叉树在数据存储,数据排序以及顺序查找当中有重大的应用。
①节点:包含一个数据元素及若干指向子树分支的信息
②节点的度:一个节点拥有子树的数目称为节点的度
③叶子节点:也称为终端节点,没有子树的节点或者度为零的节点
④分支节点:也称为非终端节点,度不为零的节点称为非终端节点
⑤树的度:树中所有节点的度的最大值
⑥节点的层次:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推,如果某一个节点位于第L层,则其子节点位于第L+1层
⑦树的深度:也称为树的高度,树中所有节点的层次最大值称为树的深度 (来自百度百科)
二叉树的遍历:有前序,中序,后序以及层序遍历,但都不够直观,能不能完整打印出一棵二叉树的形状呢?
1.灵感来源
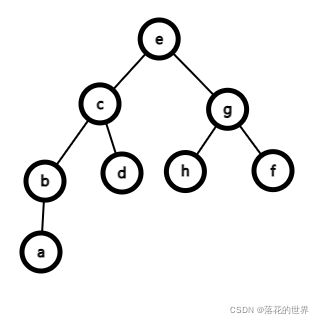
使用 “/”代表左分支,使用"\"代表右分支,上述二叉树可以表示为
e
/ \
c g
/ \ / \
b d f h
/
a
和实际二叉树很相似
2.需求
- 按照二叉树的形状打印一棵二叉树,其中二叉树节点元素的值为0~9或者英文字母
- 构建一棵二叉搜索树,进行验证
- 完成一个小算法题,参见后文
3.实现语言
python
4.基本思路
- 层序遍历:按照节点所在的位置,每一层每一层的打印节点,即先打印第一层,再打印第二层,以此类推,直到打印到最后一层结束为止。
- 在打印节点时,关键是要知道节点在打印区域对应的位置,为此,需要一个专门的list集合来记录此位置。
- 一旦某个节点在打印区域的位置确定,如果它含有左右分支节点,那么,其左右分支节点的位置实际上也可以确定。如下所示
2------>位置为x
位置为x-1<---/ \--->位置为x+1
位置为x-2<--1___3--->位置为x+2
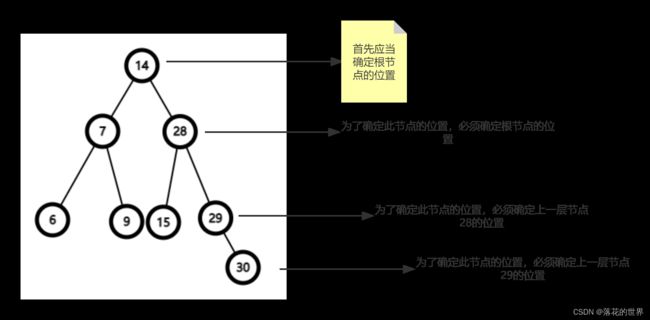
- 实际的二叉树,包含许多上述的基本单元,根据上述分析,为了确定某一个节点的位置,应当确定其父亲节点的位置,同理,为了确定其父亲节点的位置,应当先确定其父亲的父亲的节点的位置,以此递归,发现,首先应当确定其根节点的位置。
-
根节点位置确定
- 确定一棵二叉树的宽度,为了方便计算,以最后一层叶子节点为基准,确定打印二叉树时所需要预留的最小打印区域
一点简单的数学推导,对于深度为h的二叉树,其需要预留的宽度的大小为:(结合上面图)
最后一层的叶子节点的数目:2^(h-1)
相邻节点之间需要预留的位置为:3*2(h-1)+2(h-1)-1
宽度为:6*2^(h-1)-1
根节点的位置为:上述宽度再除以2
5.代码实现
- 节点类型定义
'节点类型'
def __init__(self, item):
self.item = item
self.left = None
self.right = None
- 二叉树基本属性定义和方法实现
class Tree:
'二叉树'
def __init__(self):
self.root = None
def add_node(self, root, value):
'构建二叉搜索树,向当前二叉树添加节点,返回以root为根节点的二叉树'
if root is None:
node = Node(value)
root = node
if self.root is None:
self.root = node
elif value < root.item:
root.left = self.add_node(root.left, value)
elif value > root.item:
root.right = self.add_node(root.right, value)
return root
def in_order(self, root):
'中序遍历打印二叉树信息'
if root is None:
return
self.in_order(root.left)
print(root.item)
self.in_order(root.right)
def depth(self, root):
'求二叉树的深度'
if root is None:
return 0
leftDepth = self.depth(root.left) + 1
rightDepth = self.depth(root.right) + 1
height = rightDepth
if leftDepth > rightDepth:
height = leftDepth
return height
- 核心代码,打印一棵二叉树
def print_tree(self, root):
'''
打印一棵二叉树,二叉树节点值为0~9 10个整数或者26个大小写英文字母
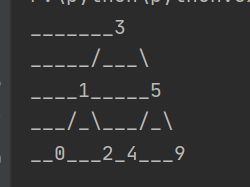
使用/\模拟左右分支,如下所示
3
/ \
1 5
/ \ / \
0 2 4 9
'''
if root is None:
return
# 基本思想:
# 查询二叉树高度,预留足够的打印区域
current = self.depth(root)
# 计算深度为depth的满二叉树需要的打印区域:叶子节点需要的打印区域,恰好为奇数
# 同一个节点左右孩子间隔 3 个空格
# 相邻节点至少间隔一个空格,
max_word = 3 * (2 ** (current - 1)) - 1
node_space = int(max_word / 2) # 每一个节点前面的空格数
# queue1和queue2用来存放节点以及节点打印时的位置
# queue1:当前层
# queue2:下一层
queue1 = [[self.root, node_space + 2]]
queue2 = []
while queue1:
# 使用i_position列表记录左右斜杠的位置
i_position = []
# 确定左右斜杠的位置
# "/"比当前节点的位置少1
# "\"比当前节点的位置多1
for i in range(len(queue1)):
node = queue1[i][0] # 节点打印位置
i_space = queue1[i][1] - 1 # 左右斜线打印位置
# 对于根节点,左右各空出1个空格
if node.item == self.root.item:
i_space -= 1
# 存储左斜线和左孩子
if node.left is not None:
i_position.append([i_space, '/'])
queue2.append([node.left, i_space - 1])
i_space += 2
if node.item == self.root.item:
i_space += 2
# 存储右斜线和右孩子
if node.right is not None:
i_position.append([i_space, '\\'])
queue2.append([node.right, i_space + 1])
# 打印节点和左右斜杠
# 打印节点
if len(queue1) > 0:
# 找到打印位置最远的节点的位置
last_node = queue1[len(queue1) - 1][1]
# 当前打印节点的数目
index = 0
for i in range(last_node + 1):
# 打印节点
if index < len(queue1) and i == queue1[index][1]:
print(queue1[index][0].item, end='')
index += 1
else:
# 打印空格
print(' ', end='')
print()
# 打印左右斜杠
index = 0
if len(i_position) > 0:
for i in range(i_position[len(i_position) - 1][0] + 1):
if i == i_position[index][0]:
print(i_position[index][1], end='')
index += 1
else:
print(' ', end='')
print()
# 更新queue1和queue2
queue1 = []
while queue2:
queue1.append(queue2.pop(0))
node_space -= 2
6.bug提示
正如前文分析提到,相邻节点之间需要留有一定的空格加以区分,随着二叉树的深度在增加,特别是当存在满二叉树时,应用上述代码,会出现如下情况:
g
/ \
d k
/ \ / \
b f i m
/ \ / / \ /
a c
在打印第四层节点时,由于打印位置存在冲突,导致,无法打印某些节点,解决的方法就是从一开始的根节点开始,其左右分支节点位置不是
2------>位置为x
位置为x-1<---/ \--->位置为x+1
位置为x-2<--1___3--->位置为x+2
而是
2------>位置为x
位置为x-2<---/ \--->位置为x+2
位置为x-3<--1 3--->位置为x+3
但是这也不是根本解决方案,由于这种方案本身存在的缺陷,导致在打印二叉树时存在下面限制:
打印一棵二叉树,二叉树节点值为0~9 10个整数或者26个大小写英文字母
但是在打印满二叉树时,最多打印三层,对于深度为4的二叉树,存在节点冲突,无法打印
如果需要跟进一步,需要借助plot等python画图工具,可能更好一点,但那比较麻烦
7.简单应用–解决算法题
功能描述:
深度为h的满二叉树的节点的个数sum为:1+2+2^2+2^(h-1)=2^h-1
h: 1 2 3 4 5 ……
sum:1 3 7 15 31 ……
给定一个序列,将其构建成对应深度的满二叉搜索树
e
/ \
c g
/ \ / \
b d f h
在这里调用上述的实现的print_tree函数,来分析每一次递归时树的变化情况。
def partition(self, array, fr, to, k):
'''
使用快排思想,在[fr,to]区间内返回第k+1小的数,即array[k+fr]
'''
middle = int(fr + (to - fr) / 2)
# 双路快速排序
self.swap(array, fr, middle)
i = fr + 1 # 左指针
j = to # 右指针
while i <= j:
while i <= j and array[i] < array[fr]:
i += 1
while i <= j and array[j] > array[fr]:
j -= 1
if i > j:
break
# array i和j值交换
self.swap(array, i, j)
i += 1
j -= 1
# j值交换
self.swap(array, fr, j)
if j == fr:
return
if j - fr == k:
return
elif j - fr < k:
# 已经找到最小的j个数
return self.partition(array, j, to, k - j)
else:
return self.partition(array, fr, j - 1, k)
def swap(self, array, i, j):
temp = array[i]
array[i] = array[j]
array[j] = temp
def traverse_(self, array, fr, to):
'''
:param array:给定序列
:param fr: 起始位置
:param to: 结束位置
:return: 递归整理序列
'''
if fr == to:
self.add_node(self.root, array[fr])
return
if fr > to:
return
# 调用partition函数,找到位于序列中间的值
middle = int((to - fr + 1) / 2)
self.partition(array, fr, to, middle)
value = array[fr + middle]
self.add_node(self.root, value)
self.print_tree(self.root)# 调用打印函数
# 开始递归,处理左右半边
self.traverse_(array, fr, fr + middle - 1)
self.print_tree(self.root)# 调用打印函数
self.traverse_(array, fr + middle + 1, to)
self.print_tree(self.root)# 调用打印函数
def traverse(self, array):
'''
功能描述:
深度为h的满二叉树的节点的个数sum为:1+2+2^2+2^(h-1)=2^h-1
h: 1 2 3 4 5 ……
sum:1 3 7 15 31 ……
给定一个序列,将其构建成对应深度的满二叉搜索树
e
/ \
c g
/ \ / \
b d f h
'''
self.traverse_(array, 0, len(array) - 1)
测试代码
list = ['a', 'b', 'c', 'd', 'e', 'f', 'g']
tree.traverse(list)
结果
d
d
/
b
d
/
b
/
a
d
/
b
/ \
a c
d
/
b
/ \
a c
d
/ \
b f
/ \
a c
d
/ \
b f
/ \ /
a c e
d
/ \
b f
/ \ / \
a c e g
8.下一期更新
maven在多模块开发时,使用profiles标签配置多环境运行时,本身存在一个小bug,目前还在等待验证和核实