python练习（散点图、直线图、线型回归、岭回归）

题目一

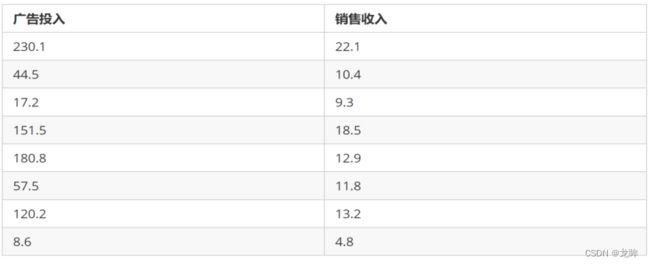
1.某公司电视广告投入和销售收入之间的关系如下表格所示。请编写代码，使用线性回归模型预测，当电视广告投入为300、400和500时，销售收入为多少？计算并打印出来。并且画出散点图和直线图。

运行代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn.linear_model as lm
# 设置显示中文字体
plt.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
plt.rcParams["axes.unicode_minus"] = False
# 导入数据
data=pd.read_csv(r'./data/data1.csv')
print(data)

x=data['Advertising_input']
x=pd.DataFrame(x.values) #把x变成二维数据
y=data['sales_revenue']

# 线型回归命令
model = lm.LinearRegression() #导入线型回归库
model.fit(x,y) #x必须为二维数据，直接求k,b
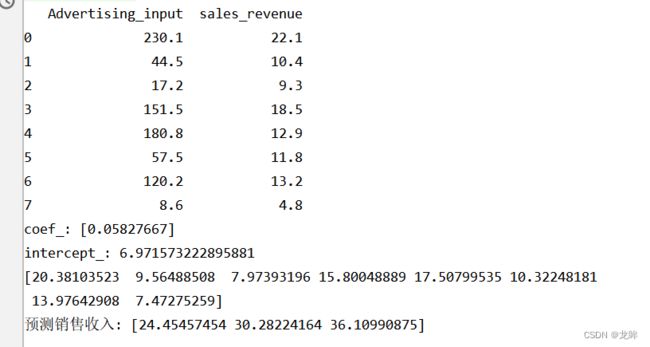
print("coef_:",model.coef_) #斜率k
print("intercept_:",model.intercept_) #截距b

pred_y=model.predict(x) #输入数据为二维
print(pred_y)

# # 绘制散点图
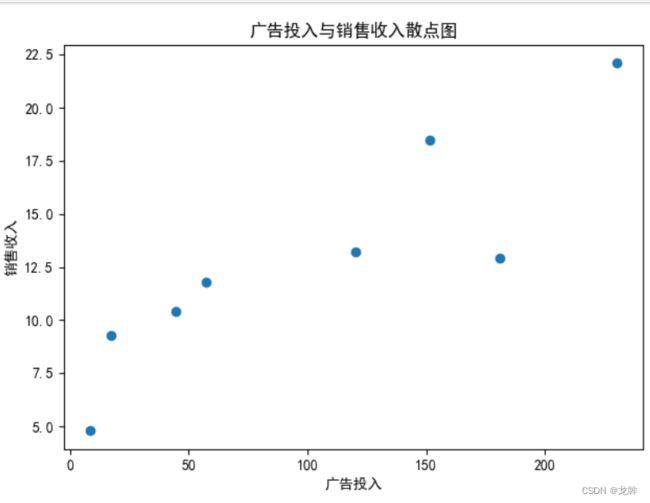
plt.scatter(x,y)
plt.xlabel('广告投入')
plt.ylabel('销售收入')
plt.title('广告投入与销售收入散点图')
plt.show()
# 模型可视化
plt.grid(linestyle=':') #网格线设置
plt.scatter(x, y)
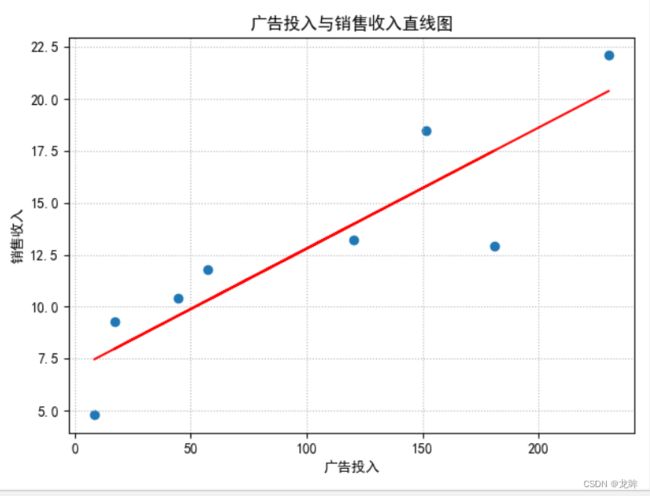
plt.plot(x, pred_y,color='r',label='LM')
plt.xlabel('广告投入')
plt.ylabel('销售收入')
plt.title('广告投入与销售收入直线图')
plt.show()

# 电视广告投入为300,400,500时,预测销售收入
x_new=model.predict([[300],[400],[500]]) #输入数据为二维
print('预测销售收入:',x_new)

运行结果

题目二

2.从某一行业中随机抽取 5 家企业，所得产品产量x(台)与生产费用y(万元)的数据如下：
x=[40,50,60,70,80,90,100,110,120,130]
y=[130,140,145,152,160,163,172,190,260,280]
请使用线性回归、岭回归等回归方法来估计上述回归方程，并且用R2得分来估计所得模型的准确程度，画出散点图和直线图并选择合适的模型来估计产品产量为140、150和160台时，生产费用是多少万元。

运行代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import sklearn.preprocessing as sp
import sklearn.linear_model as lm
import sklearn.metrics as sm #模型性能评价模块
import matplotlib.pyplot as mp
# 设置显示中文字体
plt.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
plt.rcParams["axes.unicode_minus"] = False
# 导入数据
data=pd.read_csv(r'./data/data2.csv')
print(data)
x=data['Producivity']
x=pd.DataFrame(x.values) #把x变成二维数据
y=data['Production_cost']
# # 绘制散点图
plt.scatter(x,y)
plt.xlabel('产品产量')
plt.ylabel('生产费用')
plt.title('广告投入与销售收入散点图')
plt.show()

# 线型回归命令
model = lm.LinearRegression() #导入线型回归库
model.fit(x,y) #x必须为二维数据，直接求k,b
print("coef_:",model.coef_) #斜率k
print("intercept_:",model.intercept_) #截距b

# 岭回归命令
model_2=lm.Ridge(alpha=20000,max_iter=100000) #lm.Ridge为岭回归命令
# 创建对象，alpha为正则强度,max_iter为最大迭代次数
model_2.fit(x,y) #训练
pred_y2_ridge=model_2.predict(x) #预测
pred_y=model.predict(x) #输入数据为二维的
print(pred_y)

plt.grid(linestyle=':') #网格线设置
plt.scatter(x, y)
# 线型回归的直线图
plt.plot(x, pred_y,color='r',label='LM')
# 岭回归直线图
plt.plot(x,pred_y2_ridge,color='blue',label='Ridge')
plt.legend()
plt.xlabel('产品产量')
plt.ylabel('生产费用')
plt.title('线型回归直线图与岭回归直线图')
plt.show()

#R2得分，判断拟合程度的指标，范围为[0,1],越接近1，拟合程度越好
r2=sm.r2_score(pred_y,y)
print('拟合程度指标:',r2)

# 产品产量为140,150,160时,预测生产费用多少万元
# 线型回归预测
pred_y=model.predict([[140],[150],[160]]) #输入数据为二维
print('线型回归预测生产费用:',pred_y)
# 岭回归预测
pred_y2_ridge=model_2.predict([[140],[150],[160]]) #预测
print('岭回归预测生产费用:',pred_y2_ridge)

运行结果

根据线型回归模型与岭回归模型，对产品产量预测生产费用的结果与生产进行比较，得出岭回归模型生产费用低于线型回归模型，采用岭回归模型是最合适、最省钱的模型方法。