LV小猪精

MC（移动立方体）算法

Marching Cubes（移动立方体）

Marching squares 算法
Marching Cubes算法

写在最前面：
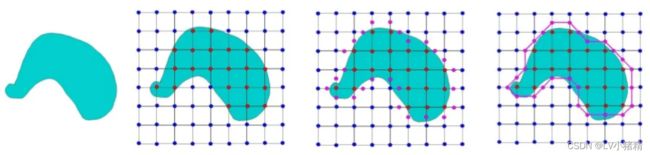
在学习MC算法之前先看看二维的MS算法，MC算法是二维MS算法的拓展，通过学习MS的基本思路能够更快学习MC算法，因此在这里我们首先提一下MS的基本算法流程。

Marching squares 算法

MS算法的主要流程：

  1. 遍历每个栅格，从16种固定情况中选择类别

  2. 利用线性插值，结合网格点数值找寻交点

  3. 根据线性插值的结果连线

具体的操作过程如图所示：

Marching Cubes算法

MC算法也被称作“等值面提取（Isosurface Extraction）”是面绘制算法中的经典算法，算法的主要精髓为：在三维离散数据场中通过线性差值来逼近等值面。
在学习MC算法前需要给定一些基本概念：首先定义一个立方体单元为一个体素，每一个体元均由8个顶点所构成。

体素顶点有两种不同的状态量所表示：

高于或等于势值表示在物体表面的内部
低于势值表示在物体表面的外部
因此，体素的一个顶点有两中可能的状态，则一个体素（8个顶点）就一共有2^8=256种状态。根据旋转、映射不变等特性，体素的状态可以被归纳为以下15种基本构型：

为了存储方便，将其记录在表中（如下所示）

int MarchingCubes::ms_edgeTable[256]={
  0x0  , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
  0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
  0x190, 0x99 , 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c,
  0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
  0x230, 0x339, 0x33 , 0x13a, 0x636, 0x73f, 0x435, 0x53c,
  0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
  0x3a0, 0x2a9, 0x1a3, 0xaa , 0x7a6, 0x6af, 0x5a5, 0x4ac,
  0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
  0x460, 0x569, 0x663, 0x76a, 0x66 , 0x16f, 0x265, 0x36c,
  0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
  0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0xff , 0x3f5, 0x2fc,
  0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
  0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x55 , 0x15c,
  0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
  0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0xcc ,
  0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
  0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc,
  0xcc , 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
  0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c,
  0x15c, 0x55 , 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
  0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc,
  0x2fc, 0x3f5, 0xff , 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
  0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c,
  0x36c, 0x265, 0x16f, 0x66 , 0x76a, 0x663, 0x569, 0x460,
  0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac,
  0x4ac, 0x5a5, 0x6af, 0x7a6, 0xaa , 0x1a3, 0x2a9, 0x3a0,
  0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c,
  0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x33 , 0x339, 0x230,
  0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c,
  0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x99 , 0x190,
  0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c,
  0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x0   };

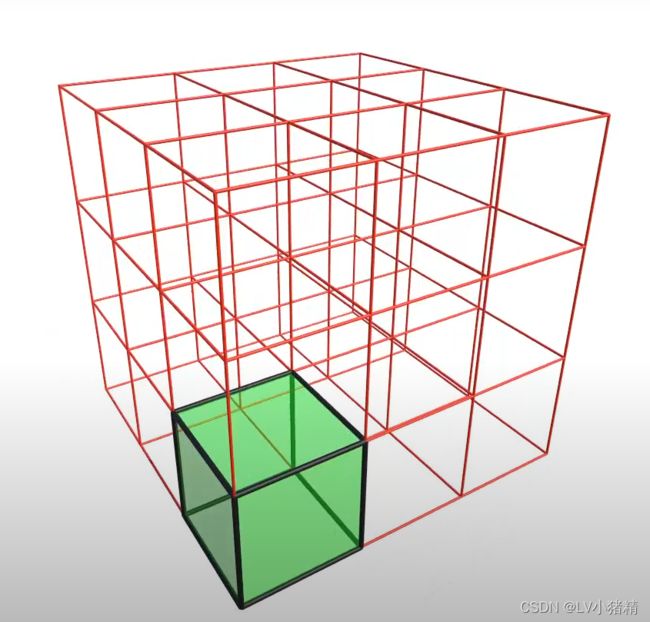
对模型包围盒空间划分体,从下到上每个体素单元均遍历一次

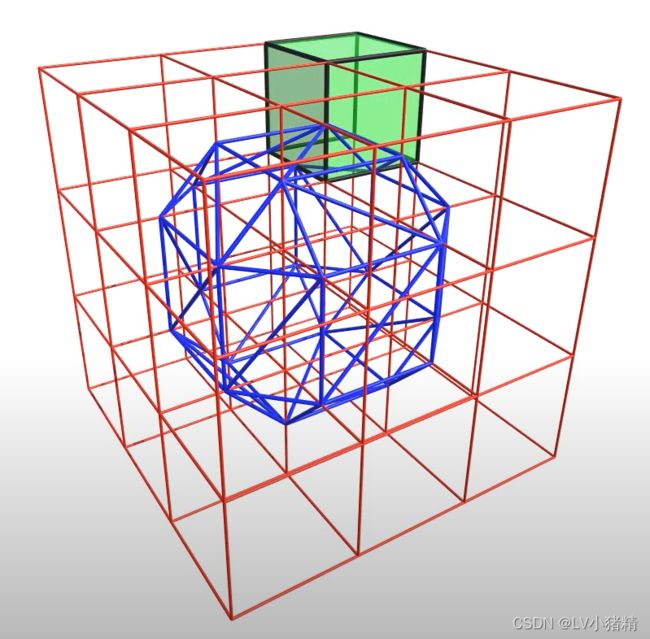
遍历完成后得到构建的模型

构建得到的三角网格模型如图所示

附上c++实现的完整代码：

// utils.h
#pragma once
#include 

#define NULL 0
#define BYTE unsigned char

template <class T> class VECTOR3 {
public:
	T x;
	T y;
	T z;

	VECTOR3(): x(0), y(0),z(0) {}
	VECTOR3(const VECTOR3<int> &other): x(other.x), y(other.y), z(other.z) {}
	VECTOR3(const T _x, const T _y, const T _z) : x(_x), y(_y), z(_z) {}

	bool operator == ( const VECTOR3<T>& other ) const {return (other.x==x && other.y==y && other.z==z); }
	bool operator != ( const VECTOR3<T>& other ) const {return (other.x!=x || other.y!=y || other.z!=z); } 

    // binary operators with scalars
	VECTOR3<T> operator + ( T scalar ) const {return VECTOR3<T>(x+scalar,y+scalar,z+scalar);}
	VECTOR3<T> operator - ( T scalar ) const {return VECTOR3<T>(x-scalar,y-scalar,z-scalar);}
	VECTOR3<T> operator * ( T scalar ) const {return VECTOR3<T>(x*scalar,y*scalar,z*scalar);}
	VECTOR3<T> operator / ( T scalar ) const {return VECTOR3<T>(x/scalar,y/scalar,z/scalar);}

	// binaray operpators  with vectors
	VECTOR3<T> operator + ( const VECTOR3<T>& other ) const {return VECTOR3<T>(x+other.x,y+other.y,z+other.z);}
	VECTOR3<T> operator - ( const VECTOR3<T>& other ) const {return VECTOR3<T>(x-other.x,y-other.y,z-other.z);}
	VECTOR3<T> operator * ( const VECTOR3<T>& other ) const {return VECTOR3<T>(x*other.x,y*other.y,z*other.z);}
	VECTOR3<T> operator / ( const VECTOR3<T>& other ) const {return VECTOR3<T>(x/other.x,y/other.y,z/other.z);}

	T maxVal() {return (x>y) ? ((x>z) ? x : z) : ((y>z) ? y : z);}
	T minVal() {return (x<y) ? ((x<z) ? x : z) : ((y<z) ? y : z);}
	T volume() {return x*y*z;}
	T length() {return sqrt(T(x*x+y*y+z*z));}
	void normalize() {T len = length(); x/=len;y/=len;;z/=len;}
	void normalize(float epsilon) {
		T len = length();
		if (len > epsilon) {
			x/=len;
			y/=len;
			z/=len;
		} else { // specify some arbitrary normal
			x = 0;
			y = 0;
			z = 1;
		}
	}
};


void loadData(char *fileName, bool bIsFloat, VECTOR3<int>* iVolSize, float **data);
void loadData(char *fileName, bool bIsFloat, VECTOR3<int> iVolSize, float **data);

//utils.cpp
#include "utils.h"
#include 
#include 
#include 


void loadData(char *fileName, bool bIsFloat, VECTOR3<int>* iVolSize, float **data) {
	printf("\nTrying to load %s Dataset...\n",fileName);

	FILE *stream;	
	if((stream = fopen(fileName, "rb"))==NULL) {
		printf("Error while loading data from file %s.\n",fileName);
		exit(0);
	} else {
		fread(iVolSize , sizeof(VECTOR3<int>), 1, stream);
		*data = new float[iVolSize->volume()];
		if (bIsFloat) {
			fread(*data, sizeof(float), iVolSize->volume(), stream);
		} else {
			BYTE* temp_data = new BYTE[iVolSize->volume()];
			fread(temp_data, sizeof(BYTE), iVolSize->volume(), stream);
			for (int i = 0;i<iVolSize->volume();i++) (*data)[i] = float(temp_data[i])/255.0f;
			delete [] temp_data;
		}

		fclose( stream );
		printf("\nData loaded\n");
	}
}

void loadData(char *fileName, bool bIsFloat, VECTOR3<int> iVolSize, float **data) {
	printf("\nTrying to load %s Dataset...\n",fileName);

	FILE *stream;	
	if((stream = fopen(fileName, "rb"))==NULL) {
		printf("Error while loading data from file %s.\n",fileName);
		exit(0);
	} else {
		*data = new float[iVolSize.volume()];
		if (bIsFloat) {
			fread(*data, sizeof(float), iVolSize.volume(), stream);
		} else {
			BYTE* temp_data = new BYTE[iVolSize.volume()];
			fread(temp_data, sizeof(BYTE), iVolSize.volume(), stream);
			for (int i = 0;i<iVolSize.volume();i++) (*data)[i] = float(temp_data[i])/255.0f;
			delete [] temp_data;
		}

		fclose( stream );
		printf("\nData loaded\n");
	}
}


//MarchingCube.h
#pragma once

#include 
#include "utils.h"

#define EPSILON 0.000001f
#define DATA_INDEX(I, J, K, IDIM, JDIM) ((I) + ((IDIM) * (J)) + ((IDIM * JDIM) * (K)))
#define EDGE_INDEX(E, I, J, IDIM) ((E) + (12 * (I)) + ((12 * (IDIM)) * (J)))
#define NO_EDGE -1

class LayerTempData 
{
private:
	VECTOR3<int> m_vVolSize;
public:
	LayerTempData(VECTOR3<int> vVolSize, float* pfVolume) 
	{
		m_vVolSize = vVolSize;
		
		pfBotData	= pfVolume;
		pfTopData	= pfVolume+DATA_INDEX(0, 0, 1, vVolSize.x, vVolSize.y);
		piEdges		= new int[(vVolSize.x-1) * (vVolSize.y-1) * 12];  // allocate storage to hold the indexing tags for edges in the layer
		
		for (int i = 0; i < (vVolSize.x-1) * (vVolSize.y-1) * 12; i++)	piEdges[i] = NO_EDGE;  // init edge list
	}
	
	virtual ~LayerTempData() 
	{
		delete [] piEdges;
		delete [] pfTopData;
		delete [] pfBotData;
	}
	
	void nextIteration() 
	{
		// update the layer for this iteration
		pfBotData = pfTopData;
		// now topData points to next layer of scalar data
		pfTopData += DATA_INDEX(0, 0, 1, m_vVolSize.x, m_vVolSize.y);
		// percolate the last layer's top edges to this layer's bottom edges
		for (int iY = 0; iY < m_vVolSize.y-1; iY++) 
		{
			for (int iX = 0; iX < m_vVolSize.x-1; iX++) 
			{
				for (int iEdges = 0; iEdges < 4; iEdges++) 
				{
					piEdges[EDGE_INDEX(iEdges, iX, iY, m_vVolSize.x-1)] =  piEdges[EDGE_INDEX(iEdges+4, iX, iY, m_vVolSize.x-1)];
				}
				// reinitialize all of the remaining edges
				for (int  iEdges = 4; iEdges < 12; iEdges++) 
				{
					piEdges[EDGE_INDEX(iEdges, iX, iY, m_vVolSize.x-1)] = NO_EDGE;
				}
			}
		}
	}
	
	float*	pfBotData;
	float*	pfTopData;
	int*	piEdges;  // tag indexing into vertex list
};

class Isosurface{
public:
	VECTOR3<float>*	vfVertices;
	VECTOR3<float>*	vfNormals;
	VECTOR3<int>*	viTriangles;
	int				iVertices;
	int				iTriangles;

	Isosurface() {
	    vfVertices  = NULL;
	    vfNormals   = NULL;
	    viTriangles = NULL;
	    iVertices   = 0;
	    iTriangles  = 0;
	}

	Isosurface(int iMaxVertices, int iMaxTris) 
	{
	    vfVertices  = new VECTOR3<float>[iMaxVertices];
	    vfNormals   = new VECTOR3<float>[iMaxVertices];
	    viTriangles = new VECTOR3<int>[iMaxTris];
	    iVertices   = 0;
	    iTriangles  = 0;
	}

	virtual ~Isosurface() 
	{
		delete [] vfVertices;
		delete [] vfNormals;
		delete [] viTriangles;
	}

	int AddTriangle(int a, int b, int c) 
	{
		viTriangles[iTriangles++] = VECTOR3<int>(a,b,c);
		return iTriangles-1;
	}

	int AddVertex(VECTOR3<float> v, VECTOR3<float> n) 
	{
		vfVertices[iVertices] = v;
		vfNormals[iVertices++] = n; 
		return iVertices-1;
	}

	void AppendData(const Isosurface* other) 
	{
		// if verts in other, expand the storage this surface
		if (other->iVertices > 0) 
		{

			// create new mem
			VECTOR3<float>*	temp_Vertices  = new VECTOR3<float>[iVertices  + other->iVertices];
			VECTOR3<float>*	temp_Normals   = new VECTOR3<float>[iVertices  + other->iVertices];
			VECTOR3<int>*	temp_Triangles = new VECTOR3<int>[iTriangles + other->iTriangles];

			// copy "old" data
			memcpy(temp_Vertices, vfVertices, sizeof(VECTOR3<float>)*iVertices);
			memcpy(temp_Normals, vfNormals, sizeof(VECTOR3<float>)*iVertices);
			memcpy(temp_Triangles, viTriangles, sizeof(VECTOR3<int>)*iTriangles);

			// append new data
			memcpy(temp_Vertices+iVertices, other->vfVertices, sizeof(VECTOR3<float>)*other->iVertices);
			memcpy(temp_Normals+iVertices, other->vfNormals, sizeof(VECTOR3<float>)*other->iVertices);
			memcpy(temp_Triangles+iTriangles, other->viTriangles, sizeof(VECTOR3<int>)*other->iTriangles);

			// delete "old" data
			delete [] vfVertices;
			delete [] vfNormals;
			delete [] viTriangles;

			// rename
			vfVertices  = temp_Vertices;
			vfNormals   = temp_Normals;
			viTriangles = temp_Triangles;
		}

		// update this list's counters
		iVertices  += other->iVertices;
		iTriangles += other->iTriangles;
	}
};


class MarchingCubes
{
protected:
	static int		ms_edgeTable[256];
	static int		ms_triTable[256][16];

	float			m_fFlipFact;
	float			m_bFlipSurface;
	VECTOR3<int>	m_vVolSize;
	float*			m_pfVolume;
	float			m_fIsoValue;

	virtual void MarchLayer(LayerTempData *layer, int iLayer);
	virtual int MakeVertex(int whichEdge, int i, int j, int k, Isosurface* sliceIso);
	virtual VECTOR3<float> InterpolateNormal(float fValueAtPos, VECTOR3<int> vPosition);

public:
	Isosurface*		m_Isosurface;
	VECTOR3<float>  BoxMin;     //网格顶点中最左下点坐标
	float           spacing;    //网格间距，这里假定三个方向的间距一致

	MarchingCubes(void);
	virtual ~MarchingCubes(void);

	virtual void SetVolume(int iSizeX, int iSizeY, int iSizeZ, float* pfVolume);
	virtual void Process(float fIsoValue, bool bFlipSurface=false);
};

//MarchingCube.cpp
#include "marchingcubes.h"
int MarchingCubes::ms_edgeTable[256]={
  0x0  , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
  0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
  0x190, 0x99 , 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c,
  0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
  0x230, 0x339, 0x33 , 0x13a, 0x636, 0x73f, 0x435, 0x53c,
  0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
  0x3a0, 0x2a9, 0x1a3, 0xaa , 0x7a6, 0x6af, 0x5a5, 0x4ac,
  0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
  0x460, 0x569, 0x663, 0x76a, 0x66 , 0x16f, 0x265, 0x36c,
  0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
  0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0xff , 0x3f5, 0x2fc,
  0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
  0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x55 , 0x15c,
  0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
  0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0xcc ,
  0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
  0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc,
  0xcc , 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
  0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c,
  0x15c, 0x55 , 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
  0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc,
  0x2fc, 0x3f5, 0xff , 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
  0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c,
  0x36c, 0x265, 0x16f, 0x66 , 0x76a, 0x663, 0x569, 0x460,
  0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac,
  0x4ac, 0x5a5, 0x6af, 0x7a6, 0xaa , 0x1a3, 0x2a9, 0x3a0,
  0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c,
  0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x33 , 0x339, 0x230,
  0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c,
  0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x99 , 0x190,
  0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c,
  0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x0   };


int MarchingCubes::ms_triTable[256][16] =
{{NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 8, 3, 9, 8, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, 1, 2, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 2, 10, 0, 2, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 8, 3, 2, 10, 8, 10, 9, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 11, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 11, 2, 8, 11, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 9, 0, 2, 3, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 11, 2, 1, 9, 11, 9, 8, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 10, 1, 11, 10, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 10, 1, 0, 8, 10, 8, 11, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 9, 0, 3, 11, 9, 11, 10, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 8, 10, 10, 8, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 7, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 3, 0, 7, 3, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, 8, 4, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 1, 9, 4, 7, 1, 7, 3, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, 8, 4, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 4, 7, 3, 0, 4, 1, 2, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 2, 10, 9, 0, 2, 8, 4, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 10, 9, 2, 9, 7, 2, 7, 3, 7, 9, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 4, 7, 3, 11, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 4, 7, 11, 2, 4, 2, 0, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 0, 1, 8, 4, 7, 2, 3, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 7, 11, 9, 4, 11, 9, 11, 2, 9, 2, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 10, 1, 3, 11, 10, 7, 8, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 11, 10, 1, 4, 11, 1, 0, 4, 7, 11, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 7, 8, 9, 0, 11, 9, 11, 10, 11, 0, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 7, 11, 4, 11, 9, 9, 11, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 4, 0, 8, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 5, 4, 1, 5, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 5, 4, 8, 3, 5, 3, 1, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, 9, 5, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 0, 8, 1, 2, 10, 4, 9, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 2, 10, 5, 4, 2, 4, 0, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 4, 2, 3, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 11, 2, 0, 8, 11, 4, 9, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 5, 4, 0, 1, 5, 2, 3, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 1, 5, 2, 5, 8, 2, 8, 11, 4, 8, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 3, 11, 10, 1, 3, 9, 5, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 9, 5, 0, 8, 1, 8, 10, 1, 8, 11, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 4, 0, 5, 0, 11, 5, 11, 10, 11, 0, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 4, 8, 5, 8, 10, 10, 8, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 7, 8, 5, 7, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 3, 0, 9, 5, 3, 5, 7, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 7, 8, 0, 1, 7, 1, 5, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 5, 3, 3, 5, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 7, 8, 9, 5, 7, 10, 1, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 1, 2, 9, 5, 0, 5, 3, 0, 5, 7, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 0, 2, 8, 2, 5, 8, 5, 7, 10, 5, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 10, 5, 2, 5, 3, 3, 5, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 9, 5, 7, 8, 9, 3, 11, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 7, 9, 7, 2, 9, 2, 0, 2, 7, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 3, 11, 0, 1, 8, 1, 7, 8, 1, 5, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 2, 1, 11, 1, 7, 7, 1, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 8, 8, 5, 7, 10, 1, 3, 10, 3, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 7, 0, 5, 0, 9, 7, 11, 0, 1, 0, 10, 11, 10, 0, NO_EDGE},
 {11, 10, 0, 11, 0, 3, 10, 5, 0, 8, 0, 7, 5, 7, 0, NO_EDGE},
 {11, 10, 5, 7, 11, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 6, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, 5, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 0, 1, 5, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 8, 3, 1, 9, 8, 5, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 6, 5, 2, 6, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 6, 5, 1, 2, 6, 3, 0, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 6, 5, 9, 0, 6, 0, 2, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 9, 8, 5, 8, 2, 5, 2, 6, 3, 2, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 3, 11, 10, 6, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 0, 8, 11, 2, 0, 10, 6, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, 2, 3, 11, 5, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 10, 6, 1, 9, 2, 9, 11, 2, 9, 8, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 3, 11, 6, 5, 3, 5, 1, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 11, 0, 11, 5, 0, 5, 1, 5, 11, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 5, 9, 6, 9, 11, 11, 9, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 10, 6, 4, 7, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 3, 0, 4, 7, 3, 6, 5, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 9, 0, 5, 10, 6, 8, 4, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 6, 5, 1, 9, 7, 1, 7, 3, 7, 9, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 1, 2, 6, 5, 1, 4, 7, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 5, 5, 2, 6, 3, 0, 4, 3, 4, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 4, 7, 9, 0, 5, 0, 6, 5, 0, 2, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 3, 9, 7, 9, 4, 3, 2, 9, 5, 9, 6, 2, 6, 9, NO_EDGE},
 {3, 11, 2, 7, 8, 4, 10, 6, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 10, 6, 4, 7, 2, 4, 2, 0, 2, 7, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, 4, 7, 8, 2, 3, 11, 5, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 2, 1, 9, 11, 2, 9, 4, 11, 7, 11, 4, 5, 10, 6, NO_EDGE},
 {8, 4, 7, 3, 11, 5, 3, 5, 1, 5, 11, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 1, 11, 5, 11, 6, 1, 0, 11, 7, 11, 4, 0, 4, 11, NO_EDGE},
 {0, 5, 9, 0, 6, 5, 0, 3, 6, 11, 6, 3, 8, 4, 7, NO_EDGE},
 {6, 5, 9, 6, 9, 11, 4, 7, 9, 7, 11, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 4, 9, 6, 4, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 10, 6, 4, 9, 10, 0, 8, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 0, 1, 10, 6, 0, 6, 4, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 3, 1, 8, 1, 6, 8, 6, 4, 6, 1, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 4, 9, 1, 2, 4, 2, 6, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 0, 8, 1, 2, 9, 2, 4, 9, 2, 6, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 2, 4, 4, 2, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 3, 2, 8, 2, 4, 4, 2, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 4, 9, 10, 6, 4, 11, 2, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 2, 2, 8, 11, 4, 9, 10, 4, 10, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 11, 2, 0, 1, 6, 0, 6, 4, 6, 1, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 4, 1, 6, 1, 10, 4, 8, 1, 2, 1, 11, 8, 11, 1, NO_EDGE},
 {9, 6, 4, 9, 3, 6, 9, 1, 3, 11, 6, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 11, 1, 8, 1, 0, 11, 6, 1, 9, 1, 4, 6, 4, 1, NO_EDGE},
 {3, 11, 6, 3, 6, 0, 0, 6, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 4, 8, 11, 6, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 10, 6, 7, 8, 10, 8, 9, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 7, 3, 0, 10, 7, 0, 9, 10, 6, 7, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 6, 7, 1, 10, 7, 1, 7, 8, 1, 8, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 6, 7, 10, 7, 1, 1, 7, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 6, 1, 6, 8, 1, 8, 9, 8, 6, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 6, 9, 2, 9, 1, 6, 7, 9, 0, 9, 3, 7, 3, 9, NO_EDGE},
 {7, 8, 0, 7, 0, 6, 6, 0, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 3, 2, 6, 7, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 3, 11, 10, 6, 8, 10, 8, 9, 8, 6, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 0, 7, 2, 7, 11, 0, 9, 7, 6, 7, 10, 9, 10, 7, NO_EDGE},
 {1, 8, 0, 1, 7, 8, 1, 10, 7, 6, 7, 10, 2, 3, 11, NO_EDGE},
 {11, 2, 1, 11, 1, 7, 10, 6, 1, 6, 7, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 9, 6, 8, 6, 7, 9, 1, 6, 11, 6, 3, 1, 3, 6, NO_EDGE},
 {0, 9, 1, 11, 6, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 8, 0, 7, 0, 6, 3, 11, 0, 11, 6, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 11, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 6, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 0, 8, 11, 7, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, 11, 7, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 1, 9, 8, 3, 1, 11, 7, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 1, 2, 6, 11, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, 3, 0, 8, 6, 11, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 9, 0, 2, 10, 9, 6, 11, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 11, 7, 2, 10, 3, 10, 8, 3, 10, 9, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 2, 3, 6, 2, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 0, 8, 7, 6, 0, 6, 2, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 7, 6, 2, 3, 7, 0, 1, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 6, 2, 1, 8, 6, 1, 9, 8, 8, 7, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 7, 6, 10, 1, 7, 1, 3, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 7, 6, 1, 7, 10, 1, 8, 7, 1, 0, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 3, 7, 0, 7, 10, 0, 10, 9, 6, 10, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 6, 10, 7, 10, 8, 8, 10, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 8, 4, 11, 8, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 6, 11, 3, 0, 6, 0, 4, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 6, 11, 8, 4, 6, 9, 0, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 4, 6, 9, 6, 3, 9, 3, 1, 11, 3, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 8, 4, 6, 11, 8, 2, 10, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, 3, 0, 11, 0, 6, 11, 0, 4, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 11, 8, 4, 6, 11, 0, 2, 9, 2, 10, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 9, 3, 10, 3, 2, 9, 4, 3, 11, 3, 6, 4, 6, 3, NO_EDGE},
 {8, 2, 3, 8, 4, 2, 4, 6, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 4, 2, 4, 6, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 9, 0, 2, 3, 4, 2, 4, 6, 4, 3, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 9, 4, 1, 4, 2, 2, 4, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 1, 3, 8, 6, 1, 8, 4, 6, 6, 10, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 1, 0, 10, 0, 6, 6, 0, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 6, 3, 4, 3, 8, 6, 10, 3, 0, 3, 9, 10, 9, 3, NO_EDGE},
 {10, 9, 4, 6, 10, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 9, 5, 7, 6, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, 4, 9, 5, 11, 7, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 0, 1, 5, 4, 0, 7, 6, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 7, 6, 8, 3, 4, 3, 5, 4, 3, 1, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 4, 10, 1, 2, 7, 6, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 11, 7, 1, 2, 10, 0, 8, 3, 4, 9, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 6, 11, 5, 4, 10, 4, 2, 10, 4, 0, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 4, 8, 3, 5, 4, 3, 2, 5, 10, 5, 2, 11, 7, 6, NO_EDGE},
 {7, 2, 3, 7, 6, 2, 5, 4, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 4, 0, 8, 6, 0, 6, 2, 6, 8, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 6, 2, 3, 7, 6, 1, 5, 0, 5, 4, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 2, 8, 6, 8, 7, 2, 1, 8, 4, 8, 5, 1, 5, 8, NO_EDGE},
 {9, 5, 4, 10, 1, 6, 1, 7, 6, 1, 3, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 6, 10, 1, 7, 6, 1, 0, 7, 8, 7, 0, 9, 5, 4, NO_EDGE},
 {4, 0, 10, 4, 10, 5, 0, 3, 10, 6, 10, 7, 3, 7, 10, NO_EDGE},
 {7, 6, 10, 7, 10, 8, 5, 4, 10, 4, 8, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 9, 5, 6, 11, 9, 11, 8, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 6, 11, 0, 6, 3, 0, 5, 6, 0, 9, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 11, 8, 0, 5, 11, 0, 1, 5, 5, 6, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {6, 11, 3, 6, 3, 5, 5, 3, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 10, 9, 5, 11, 9, 11, 8, 11, 5, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 11, 3, 0, 6, 11, 0, 9, 6, 5, 6, 9, 1, 2, 10, NO_EDGE},
 {11, 8, 5, 11, 5, 6, 8, 0, 5, 10, 5, 2, 0, 2, 5, NO_EDGE},
 {6, 11, 3, 6, 3, 5, 2, 10, 3, 10, 5, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 8, 9, 5, 2, 8, 5, 6, 2, 3, 8, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 5, 6, 9, 6, 0, 0, 6, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 5, 8, 1, 8, 0, 5, 6, 8, 3, 8, 2, 6, 2, 8, NO_EDGE},
 {1, 5, 6, 2, 1, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 3, 6, 1, 6, 10, 3, 8, 6, 5, 6, 9, 8, 9, 6, NO_EDGE},
 {10, 1, 0, 10, 0, 6, 9, 5, 0, 5, 6, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 3, 8, 5, 6, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 5, 6, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 5, 10, 7, 5, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 5, 10, 11, 7, 5, 8, 3, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 11, 7, 5, 10, 11, 1, 9, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 7, 5, 10, 11, 7, 9, 8, 1, 8, 3, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 1, 2, 11, 7, 1, 7, 5, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, 1, 2, 7, 1, 7, 5, 7, 2, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 7, 5, 9, 2, 7, 9, 0, 2, 2, 11, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {7, 5, 2, 7, 2, 11, 5, 9, 2, 3, 2, 8, 9, 8, 2, NO_EDGE},
 {2, 5, 10, 2, 3, 5, 3, 7, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 2, 0, 8, 5, 2, 8, 7, 5, 10, 2, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 0, 1, 5, 10, 3, 5, 3, 7, 3, 10, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 8, 2, 9, 2, 1, 8, 7, 2, 10, 2, 5, 7, 5, 2, NO_EDGE},
 {1, 3, 5, 3, 7, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 7, 0, 7, 1, 1, 7, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 0, 3, 9, 3, 5, 5, 3, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 8, 7, 5, 9, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 8, 4, 5, 10, 8, 10, 11, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 0, 4, 5, 11, 0, 5, 10, 11, 11, 3, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 9, 8, 4, 10, 8, 10, 11, 10, 4, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {10, 11, 4, 10, 4, 5, 11, 3, 4, 9, 4, 1, 3, 1, 4, NO_EDGE},
 {2, 5, 1, 2, 8, 5, 2, 11, 8, 4, 5, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 4, 11, 0, 11, 3, 4, 5, 11, 2, 11, 1, 5, 1, 11, NO_EDGE},
 {0, 2, 5, 0, 5, 9, 2, 11, 5, 4, 5, 8, 11, 8, 5, NO_EDGE},
 {9, 4, 5, 2, 11, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 5, 10, 3, 5, 2, 3, 4, 5, 3, 8, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {5, 10, 2, 5, 2, 4, 4, 2, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 10, 2, 3, 5, 10, 3, 8, 5, 4, 5, 8, 0, 1, 9, NO_EDGE},
 {5, 10, 2, 5, 2, 4, 1, 9, 2, 9, 4, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 4, 5, 8, 5, 3, 3, 5, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 4, 5, 1, 0, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {8, 4, 5, 8, 5, 3, 9, 0, 5, 0, 3, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 4, 5, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 11, 7, 4, 9, 11, 9, 10, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 8, 3, 4, 9, 7, 9, 11, 7, 9, 10, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 10, 11, 1, 11, 4, 1, 4, 0, 7, 4, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 1, 4, 3, 4, 8, 1, 10, 4, 7, 4, 11, 10, 11, 4, NO_EDGE},
 {4, 11, 7, 9, 11, 4, 9, 2, 11, 9, 1, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 7, 4, 9, 11, 7, 9, 1, 11, 2, 11, 1, 0, 8, 3, NO_EDGE},
 {11, 7, 4, 11, 4, 2, 2, 4, 0, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {11, 7, 4, 11, 4, 2, 8, 3, 4, 3, 2, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 9, 10, 2, 7, 9, 2, 3, 7, 7, 4, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 10, 7, 9, 7, 4, 10, 2, 7, 8, 7, 0, 2, 0, 7, NO_EDGE},
 {3, 7, 10, 3, 10, 2, 7, 4, 10, 1, 10, 0, 4, 0, 10, NO_EDGE},
 {1, 10, 2, 8, 7, 4, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 9, 1, 4, 1, 7, 7, 1, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 9, 1, 4, 1, 7, 0, 8, 1, 8, 7, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 0, 3, 7, 4, 3, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {4, 8, 7, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 10, 8, 10, 11, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 0, 9, 3, 9, 11, 11, 9, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 1, 10, 0, 10, 8, 8, 10, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 1, 10, 11, 3, 10, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 2, 11, 1, 11, 9, 9, 11, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 0, 9, 3, 9, 11, 1, 2, 9, 2, 11, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 2, 11, 8, 0, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {3, 2, 11, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 3, 8, 2, 8, 10, 10, 8, 9, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {9, 10, 2, 0, 9, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {2, 3, 8, 2, 8, 10, 0, 1, 8, 1, 10, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 10, 2, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {1, 3, 8, 9, 1, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 9, 1, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {0, 3, 8, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE},
 {NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE, NO_EDGE}};

MarchingCubes::MarchingCubes(void)
{
	m_vVolSize		= VECTOR3<int>(0,0,0);
	m_pfVolume		= NULL;
	m_Isosurface	= NULL;
}

MarchingCubes::~MarchingCubes(void)
{
	if (m_Isosurface)
	{
		m_Isosurface=NULL;
		delete m_Isosurface;
	}
	if (m_pfVolume)
	{
		m_pfVolume = NULL;
		delete m_pfVolume;
	}
	
}

void MarchingCubes::SetVolume(int iSizeX, int iSizeY, int iSizeZ, float* pfVolume) 
{
	m_pfVolume	= pfVolume;
	m_vVolSize	= VECTOR3<int>(iSizeX, iSizeY, iSizeZ);
	m_fIsoValue = 0;
}

void MarchingCubes::Process(float fIsoValue, bool bFlipSurface)
{
	// sometimes it makes sense to flip the surface bFlipSurface controls this
	m_fFlipFact = (bFlipSurface) ? -0.5f : 0.5f;
	m_bFlipSurface = bFlipSurface;

	// store isovalue
	m_fIsoValue = fIsoValue;

	// init isosurface data
	if(m_Isosurface)
	{
		m_Isosurface=NULL;
	}
	delete m_Isosurface;
	m_Isosurface = new Isosurface();

	// if the volume is empty we are done
	if (m_vVolSize.volume() == 0) return;

	// create a new layer - dataset
	LayerTempData* layerData = new LayerTempData(m_vVolSize,m_pfVolume);

	// march the first layer
	MarchLayer(layerData, 0);

	// now do the remaining layers
//#pragma omp parallel for
	for (int iZ = 1; iZ < m_vVolSize.z - 1; iZ++) 
	{
		// prepare the temp data to be used in the next layer
		layerData->nextIteration();
		// march the next layer
		MarchLayer(layerData, iZ);
	}

	// delete the layer dataset
	if (layerData)
	{
		layerData=NULL;
		delete layerData;
	}
}


void MarchingCubes::MarchLayer(LayerTempData *layer, int iLayer) 
{
	double UNDEF=1e+30;
	int cellVerts[12];	// the 12 possible vertices in a cell
	for (int i = 0; i < 12; i++) cellVerts[i] = NO_EDGE;
	
	// local part of the isosurface with at most 12 vertices and at most 5 triangles per cell
	Isosurface* sliceIsosurface = new Isosurface((m_vVolSize.x-1) * (m_vVolSize.y-1) * 12, 
		(m_vVolSize.x-1) * (m_vVolSize.y-1) * 5);
	
	// march all cells in the layer
	for(int  i = 0; i < m_vVolSize.x-1; i++) 
	{
		for(int j = 0; j < m_vVolSize.y-1; j++) 
		{
			
			// fetch data from the volume
			float fVolumeValues[8];
			fVolumeValues[0] = layer->pfBotData[(j+1)	* m_vVolSize.x +		i];
			fVolumeValues[1] = layer->pfBotData[(j+1)	* m_vVolSize.x +	i + 1];
			fVolumeValues[2] = layer->pfBotData[j		* m_vVolSize.x +	i + 1];
			fVolumeValues[3] = layer->pfBotData[j		* m_vVolSize.x +		i];
			fVolumeValues[4] = layer->pfTopData[(j+1)	* m_vVolSize.x +		i];
			fVolumeValues[5] = layer->pfTopData[(j+1)	* m_vVolSize.x +	i + 1];
			fVolumeValues[6] = layer->pfTopData[j		* m_vVolSize.x +	i + 1];
			fVolumeValues[7] = layer->pfTopData[j		* m_vVolSize.x +		i];
			
			bool wu;
			wu=false;
			for (int kk=0;kk<8;kk++)
			{
				if(fVolumeValues[kk]>UNDEF) 
				{
					wu=true;
					break;
				}
			}
			if(wu) continue;
			// compute the index for the table lookup
			int cellIndex = 1*(fVolumeValues[0] < m_fIsoValue)+
				2*(fVolumeValues[1] < m_fIsoValue)+
				4*(fVolumeValues[2] < m_fIsoValue)+
				8*(fVolumeValues[3] < m_fIsoValue)+
				16*(fVolumeValues[4] < m_fIsoValue)+
				32*(fVolumeValues[5] < m_fIsoValue)+
				64*(fVolumeValues[6] < m_fIsoValue)+
				128*(fVolumeValues[7] < m_fIsoValue);
			
			// get the coordinates for the vertices, compute the triangulation and interpolate the normals
			if (ms_edgeTable[cellIndex] &    1) 
			{
				if (layer->piEdges[EDGE_INDEX(0, i, j, m_vVolSize.x-1)] == NO_EDGE)
				{     
					cellVerts[0]  = m_Isosurface->iVertices + MakeVertex(0, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[0] = layer->piEdges[EDGE_INDEX(0, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    2) 
			{
				if (layer->piEdges[EDGE_INDEX(1, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[1]  = m_Isosurface->iVertices+MakeVertex(1, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[1] = layer->piEdges[EDGE_INDEX(1, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    4) 
			{
				if (layer->piEdges[EDGE_INDEX(2, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[2]  = m_Isosurface->iVertices +MakeVertex(2, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[2] = layer->piEdges[EDGE_INDEX(2, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    8) 
			{
				if (layer->piEdges[EDGE_INDEX(3, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[3]  = m_Isosurface->iVertices+MakeVertex(3, i, j, iLayer, sliceIsosurface);
				} 
				else
				{
					cellVerts[3] = layer->piEdges[EDGE_INDEX(3, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    16) {
				if (layer->piEdges[EDGE_INDEX(4, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[4]  = m_Isosurface->iVertices+MakeVertex(4, i, j, iLayer, sliceIsosurface);
				} 
				else
				{
					cellVerts[4] = layer->piEdges[EDGE_INDEX(4, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    32)
			{
				if (layer->piEdges[EDGE_INDEX(5, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[5]  = m_Isosurface->iVertices+MakeVertex(5, i, j, iLayer, sliceIsosurface);
				}
				else 
				{
					cellVerts[5] = layer->piEdges[EDGE_INDEX(5, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    64) 
			{
				if (layer->piEdges[EDGE_INDEX(6, i, j, m_vVolSize.x-1)] == NO_EDGE)
				{     
					cellVerts[6]  = m_Isosurface->iVertices +MakeVertex(6, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[6] = layer->piEdges[EDGE_INDEX(6, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    128) 
			{
				if (layer->piEdges[EDGE_INDEX(7, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[7]  = m_Isosurface->iVertices +MakeVertex(7, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[7] = layer->piEdges[EDGE_INDEX(7, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    256) 
			{
				if (layer->piEdges[EDGE_INDEX(8, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[8]  = m_Isosurface->iVertices +MakeVertex(8, i, j, iLayer, sliceIsosurface);
				}
				else 
				{
					cellVerts[8] = layer->piEdges[EDGE_INDEX(8, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    512) 
			{
				if (layer->piEdges[EDGE_INDEX(9, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[9]  = m_Isosurface->iVertices +MakeVertex(9, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[9] = layer->piEdges[EDGE_INDEX(9, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    1024) 
			{
				if (layer->piEdges[EDGE_INDEX(10, i, j, m_vVolSize.x-1)] == NO_EDGE) 
				{     
					cellVerts[10]  = m_Isosurface->iVertices +MakeVertex(10, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[10] = layer->piEdges[EDGE_INDEX(10, i, j, m_vVolSize.x-1)];
				}
			}
			if (ms_edgeTable[cellIndex] &    2048) 
			{
				if (layer->piEdges[EDGE_INDEX(11, i, j, m_vVolSize.x-1)] == NO_EDGE)
				{     
					cellVerts[11]  = m_Isosurface->iVertices +MakeVertex(11, i, j, iLayer, sliceIsosurface);
				} 
				else 
				{
					cellVerts[11] = layer->piEdges[EDGE_INDEX(11, i, j, m_vVolSize.x-1)];
				}
			}
			
			// put the cellVerts tags into this cell's layer->edges table
			for (int iEdge = 0; iEdge < 12; iEdge++) 
			{
				if (cellVerts[iEdge] != NO_EDGE) 
				{
					layer->piEdges[EDGE_INDEX(iEdge, i, j, m_vVolSize.x-1)] = cellVerts[iEdge];
				}
			}
			
			// now propagate the vertex/normal tags to the adjacent cells to 
			// the right and behind in this layer. 
			if (i < m_vVolSize.x - 2) 
			{ // we should propagate to the right
				layer->piEdges[EDGE_INDEX( 3, i+1, j, m_vVolSize.x-1)] = cellVerts[1];
				layer->piEdges[EDGE_INDEX( 7, i+1, j, m_vVolSize.x-1)] = cellVerts[5];
				layer->piEdges[EDGE_INDEX( 8, i+1, j, m_vVolSize.x-1)] = cellVerts[9];
				layer->piEdges[EDGE_INDEX(11, i+1, j, m_vVolSize.x-1)] = cellVerts[10];
			}
			
			if (j < m_vVolSize.y - 2) 
			{ // we should propagate to the rear
				layer->piEdges[EDGE_INDEX( 2, i, j+1, m_vVolSize.x-1)] = cellVerts[0];
				layer->piEdges[EDGE_INDEX( 6, i, j+1, m_vVolSize.x-1)] = cellVerts[4];
				layer->piEdges[EDGE_INDEX(11, i, j+1, m_vVolSize.x-1)] = cellVerts[8];
				layer->piEdges[EDGE_INDEX(10, i, j+1, m_vVolSize.x-1)] = cellVerts[9];      
			}      
			
			// store the vertex indices in the triangle data structure
			int iTableIndex = 0;
			if (m_bFlipSurface)
				while (ms_triTable[cellIndex][iTableIndex] != -1) 
				{
					sliceIsosurface->AddTriangle(cellVerts[ms_triTable[cellIndex][iTableIndex+2]],
						cellVerts[ms_triTable[cellIndex][iTableIndex+1]],
						cellVerts[ms_triTable[cellIndex][iTableIndex+0]]);
					iTableIndex+=3;
				}
			else
				while (ms_triTable[cellIndex][iTableIndex] != -1) 
				{
					sliceIsosurface->AddTriangle(cellVerts[ms_triTable[cellIndex][iTableIndex+0]],
						cellVerts[ms_triTable[cellIndex][iTableIndex+1]],
						cellVerts[ms_triTable[cellIndex][iTableIndex+2]]);
					iTableIndex+=3;
				}
					
		}
	}
	
	// add this layer's triangles to the global list
	m_Isosurface->AppendData(sliceIsosurface);
	
	delete sliceIsosurface;
}

int MarchingCubes::MakeVertex(int iEdgeIndex, int i, int j, int k, Isosurface* sliceIso) 
{

	VECTOR3<int>  vFrom; // first grid vertex
	VECTOR3<int>  vTo; // second grid vertex

	// on the edge index decide what the edges are
	switch (iEdgeIndex) 
	{
		case 0: vFrom	= VECTOR3<int>(i,j+1,k);	vTo	= VECTOR3<int>(i+1,j+1,k);	break;
		case 1: vFrom	= VECTOR3<int>(i+1,j+1,k);	vTo	= VECTOR3<int>(i+1,j,k);	break;
		case 2: vFrom	= VECTOR3<int>(i+1,j,k);	vTo	= VECTOR3<int>(i,j,k);		break;
		case 3: vFrom	= VECTOR3<int>(i,j,k);		vTo	= VECTOR3<int>(i,j+1,k);	break;
		case 4: vFrom	= VECTOR3<int>(i,j+1,k+1);	vTo	= VECTOR3<int>(i+1,j+1,k+1);break;
		case 5: vFrom	= VECTOR3<int>(i+1,j+1,k+1);vTo	= VECTOR3<int>(i+1,j,k+1);	break;
		case 6: vFrom	= VECTOR3<int>(i+1,j,k+1);	vTo	= VECTOR3<int>(i,j,k+1);	break;
		case 7: vFrom	= VECTOR3<int>(i,j,k+1);	vTo	= VECTOR3<int>(i,j+1,k+1);	break;
		case 8: vFrom	= VECTOR3<int>(i,j+1,k);	vTo	= VECTOR3<int>(i,j+1,k+1);	break;
		case 9: vFrom	= VECTOR3<int>(i+1,j+1,k);	vTo	= VECTOR3<int>(i+1,j+1,k+1);break;
		case 10:vFrom	= VECTOR3<int>(i+1,j,k);	vTo	= VECTOR3<int>(i+1,j,k+1);	break;
		case 11:vFrom	= VECTOR3<int>(i,j,k);		vTo	= VECTOR3<int>(i,j,k+1);	break;
	}

	float fFromValue = m_pfVolume[DATA_INDEX(vFrom.x, vFrom.y, vFrom.z, m_vVolSize.x, m_vVolSize.y)];
	float fToValue   = m_pfVolume[DATA_INDEX(vTo.x, vTo.y, vTo.z, m_vVolSize.x, m_vVolSize.y)];

	// determine the relative distance along edge vFrom->vTo that the isosurface vertex lies
	float d = ( fFromValue - m_fIsoValue) / ( fFromValue - fToValue );
	if (d < EPSILON) {	d = 0.0f;} else if (d > (1 - EPSILON)) {d = 1.0f;}

	VECTOR3<float> startP, endP;   //对应于vFrom和 vTo的绝对坐标
	startP = VECTOR3<float>(BoxMin.x+vFrom.x*spacing, BoxMin.y+vFrom.y*spacing, BoxMin.z+vFrom.z*spacing);
	endP =   VECTOR3<float>(BoxMin.x+vTo.x*spacing, BoxMin.y+vTo.y*spacing, BoxMin.z+vTo.z*spacing);

	// interqpolate the vertex
	VECTOR3<float>	vVertex = VECTOR3<float>(startP.x + d * (endP.x - startP.x), startP.y + d * (endP.y - startP.y), startP.z + d * (endP.z - startP.z));

	// now determine the gradients at the endpoints of the edge 
	// and interpolate the normal for the isosurface vertex     
	VECTOR3<float>	vNormFrom = InterpolateNormal(fFromValue,vFrom);
	VECTOR3<float>	vNormTo   = InterpolateNormal(fToValue,vTo);

	// interpolate the normal
	VECTOR3<float>	vNormal = VECTOR3<float>(float(vNormFrom.x) + d * float(vNormTo.x - vNormFrom.x),
											 float(vNormFrom.y) + d * float(vNormTo.y - vNormFrom.y),
											 float(vNormFrom.z) + d * float(vNormTo.z - vNormFrom.z));
	vNormal.normalize(EPSILON);

	// insert the vertex and normal into the isosurface structure and return the index for this vertex
	return sliceIso->AddVertex(vVertex, vNormal);
}


VECTOR3<float> MarchingCubes::InterpolateNormal(float fValueAtPos, VECTOR3<int> vPosition) {
	// the gradients are computed by central differences, except
	// on the boundaries of the dataset, where forward or backward
	// differencing is used (three point form)
	
	VECTOR3<float> result;
	
	// the x component
	if (vPosition.x == 0) 
	{							// left border -> forward diff
		result.x = m_fFlipFact * (-3.0f * fValueAtPos + 
			4.0f * m_pfVolume[DATA_INDEX(vPosition.x+1, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)] +
			-1.0f * m_pfVolume[DATA_INDEX(vPosition.x+2, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	}
	else if (vPosition.x == m_vVolSize.x - 1) 
	{	// right border -> forward diff
		result.x = m_fFlipFact * (  3.0f * fValueAtPos+
			-4.0f * m_pfVolume[DATA_INDEX(vPosition.x-1, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)] +
			1.0f * m_pfVolume[DATA_INDEX(vPosition.x-2, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	}
	else 
	{									// interior -> central diff
		result.x = m_fFlipFact * (	m_pfVolume[DATA_INDEX(vPosition.x+1, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)] -
			m_pfVolume[DATA_INDEX(vPosition.x-1, vPosition.y, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	}
	
	// the y component
	if (vPosition.y == 0)
	{							//forward diff
		result.y = m_fFlipFact * (-3.0f * fValueAtPos + 
			4.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y+1, vPosition.z, m_vVolSize.x, m_vVolSize.y)] +
			-1.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y+2, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	} 
	else if (vPosition.y == m_vVolSize.y - 1) 
	{	// forward diff
		result.y = m_fFlipFact * (  3.0f * fValueAtPos+
			-4.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y-1, vPosition.z, m_vVolSize.x, m_vVolSize.y)] +
			1.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y-2, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	}
	else 
	{									// central diff
		result.y = m_fFlipFact * (	m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y+1, vPosition.z, m_vVolSize.x, m_vVolSize.y)] -
			m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y-1, vPosition.z, m_vVolSize.x, m_vVolSize.y)]);
	}
	
	// the z componentk
	if (vPosition.z == 0) 
	{							//forward diff
		result.z = m_fFlipFact * (-3.0f * fValueAtPos + 
			4.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z+1, m_vVolSize.x, m_vVolSize.y)] +
			-1.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z+2, m_vVolSize.x, m_vVolSize.y)]);
	} 
	else if (vPosition.z == m_vVolSize.z - 1) 
	{	// forward diff
		result.z = m_fFlipFact * (  3.0f * fValueAtPos+
			-4.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z-1, m_vVolSize.x, m_vVolSize.y)] +
			1.0f * m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z-2, m_vVolSize.x, m_vVolSize.y)]);
	}
	else 
	{									// central diff
		result.z = m_fFlipFact * (	m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z+1, m_vVolSize.x, m_vVolSize.y)] -
			m_pfVolume[DATA_INDEX(vPosition.x, vPosition.y, vPosition.z-1, m_vVolSize.x, m_vVolSize.y)]);
	}
	
	return result;
}

一些模型重构的案例：

圆环

斯坦福兔子

小猫

你可能感兴趣的:(算法,计算机图形学,MC算法,移动立方体,网格重构)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
linux中sdl的使用教程,sdl使用入门 Melissa Corvinus linux中sdl的使用教程
本文通过一个简单示例讲解SDL的基本使用流程。示例中展示一个窗口，窗口里面有个随机颜色快随机移动。当我们鼠标点击关闭按钮时间窗口关闭。基本步骤如下：1.初始化SDL并创建一个窗口。SDL_Init()初始化SDL_CreateWindow()创建窗口2.纹理渲染存储RGB和存储纹理的区别：比如一个从左到右由红色渐变到蓝色的矩形，用存储RGB的话就需要把矩形中每个点的具体颜色值存储下来；而纹理只是一
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
《度五行》生活报报甲午62：不通痛苦，太通也痛苦，要健康快乐，需要通体舒畅。 YangduSam2021
220809壬寅戊申甲午，《度.生活五行》:天干土克水，水生木，木克土。地支寅申冲，寅午合。20220809，周二，兴大上海六班2512天，西交大2013上海班3212天，后TA15332天，度生活619天，今天拜访了一家有趣且当红产业的新创公司AK。AK一开始从事深海新能源储存与供电设备的研发生产制造，2年前开始做移动与家庭储能设备的研发生产制造。觉得有趣是因为这是笔者认知里用科技做降维打击的公
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
Linux vi常用命令 fengyehongWorld Linux linux
参考资料viコマンド（vimコマンド）リファレンス目录一.保存系命令二.删除系命令三.移动系命令四.复制粘贴系命令一.保存系命令⏹保存并退出:wq⏹强制保存并退出:wq!⏹退出(文件未编辑):q⏹强制退出(忽略已编辑内容):q!⏹另存为:w新文件名二.删除系命令⏹删除当前行dd⏹清空整个文档gg：移动到文档顶部dG：删除到最后一行ggdG三.移动系命令⏹移动到文档顶部gg⏹移动到文档底部#方式1G
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
用Python实现读取统计单词个数程序媛了了 python 游戏 java
完整实例代码：fromcollectionsimportCounterdefpythonit():danci={}withopen("pythonit.txt","r",encoding="utf-8")asf:foriinf:words=i.strip().split()forwordinwords:ifwordnotindanci:danci[word]=1else:danci[word]+=
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
Python算法L5：贪心算法小熊同学哦 Python算法算法 python 贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
【ARM Cortex-M 系列 2.3 -- Cortex-M7 Debug event 详细介绍】主公讲 ARM #ARM 系列 arm开发 debug event
请阅读【嵌入式开发学习必备专栏】文章目录Cortex-M7DebugeventDebugeventsCortex-M7Debugevent在ARMCortex-M7架构中，调试事件（DebugEvent）是由于调试原因而触发的事件。一个调试事件会导致以下几种情况之一发生：进入调试状态：如果启用了停滞调试（HaltingDebug），一个调试事件会使处理器在调试状态下停滞。通过将DHCSR.C_DE
3286、穿越网格图的安全路径 Lenyiin 题解 c++算法 leetcode
3286、[中等]穿越网格图的安全路径1、题目描述给你一个mxn的二进制矩形grid和一个整数health表示你的健康值。你开始于矩形的左上角(0,0)，你的目标是矩形的右下角(m-1,n-1)。你可以在矩形中往上下左右相邻格子移动，但前提是你的健康值始终是正数。对于格子(i,j)，如果grid[i][j]=1，那么这个格子视为不安全的，会使你的健康值减少1。如果你可以到达最终的格子，请你返回tr
Python多线程实现大规模数据集高效转移 sand&wich 网络 python 服务器
背景在处理大规模数据集时，通常需要在不同存储设备、不同服务器或文件夹之间高效地传输数据。如果采用单线程传输方式，当数据量非常大时，整个过程会非常耗时。因此，通过多线程并行处理可以大幅提升数据传输效率。本文将分享一个基于Python多线程实现的高效数据传输工具，通过遍历源文件夹中的所有文件，将它们移动到目标文件夹。工具和库这个数据集转移工具主要依赖于以下Python标准库：os：用于文件系统操作，如
ubuntu安装wordpress lissettecarlr
1安装nginx网上安装方式很多，这就就直接用apt-get了apt-getinstallnginx不用启动啥，然后直接在浏览器里面输入IP:80就能看到nginx的主页了。如果修改了一些配置可以使用下列命令重启一下systemctlrestartnginx.service2安装mysql输入安装前也可以更新一下软件源，在安装过程中将会让你输入数据库的密码。sudoapt-getinstallmy
【RabbitMQ 项目】服务端：数据管理模块之绑定管理月夜星辉雪 rabbitmq 分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
非对称加密算法原理与应用2——RSA私钥加密文件私语茶馆云部署与开发架构及产品灵感记录 RSA2048 私钥加密
作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能 matlab 算法
在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
最简单将静态网页挂载到服务器上(不用nginx) 全能全知者服务器 nginx 运维前端 html 笔记
最简单将静态网页挂载到服务器上(不用nginx)如果随便弄个静态网页挂在服务器都要用nignx就太麻烦了，所以直接使用Apache来搭建一些简单前端静态网页会相对方便很多检查Web服务器服务状态：sudosystemctlstatushttpd#ApacheWeb服务器如果发现没有安装web服务器：安装Apache：sudoyuminstallhttpd启动Apache：sudosystemctl
非对称加密算法————RSA理论及详情 hu19930613
转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
c++ 内存处理函数 heeheeai c++开发语言
在C语言的头文件中，memcpy和memmove函数都用于复制内存块，但它们在处理内存重叠方面存在关键区别：内存重叠:memcpy函数不保证在源内存和目标内存区域重叠时能够正确复制数据。如果内存区域重叠，memcpy的行为是未定义的，可能会导致数据损坏或程序崩溃。memmove函数能够安全地处理源内存和目标内存区域重叠的情况。它会确保在复制过程中不会覆盖尚未复制的数据，从而保证数据的完整性。效率:
JVM StackMapTable 属性的作用及理解 lijingyao8206 jvm 字节码 Class文件 StackMapTable
在Java 6版本之后JVM引入了栈图(Stack Map Table)概念。为了提高验证过程的效率，在字节码规范中添加了Stack Map Table属性，以下简称栈图，其方法的code属性中存储了局部变量和操作数的类型验证以及字节码的偏移量。也就是一个method需要且仅对应一个Stack Map Table。在Java 7版
回调函数调用方法百合不是茶 java
最近在看大神写的代码时,.发现其中使用了很多的回调 ,以前只是在学习的时候经常用到 ,现在写个笔记记录一下代码很简单: MainDemo :调用方法得到方法的返回结果
[时间机器]制造时间机器需要一些材料 comsci 制造
根据我的计算和推测,要完全实现制造一台时间机器,需要某些我们这个世界不存在的物质和材料... 甚至可以这样说,这种材料和物质,我们在反应堆中也无法获得......
开口埋怨不如闭口做事邓集海邓集海做人做事工作
“开口埋怨，不如闭口做事。”不是名人名言，而是一个普通父亲对儿子的训导。但是，因为这句训导，这位普通父亲却造就了一个名人儿子。这位普通父亲造就的名人儿子，叫张明正。　　　　张明正出身贫寒，读书时成绩差，常挨老师批评。高中毕业，张明正连普通大学的分数线都没上。高考成绩出来后，平时开口怨这怨那的张明正，不从自身找原因，而是不停地埋怨自己家庭条件不好、埋怨父母没有给他创造良好的学习环境。　　　　
jQuery插件开发全解析，类级别与对象级别开发 IT独行者 jquery 开发插件　函数
jQuery插件的开发包括两种：一种是类级别的插件开发，即给 jQuery添加新的全局函数，相当于给 jQuery类本身添加方法。 jQuery的全局函数就是属于 jQuery命名空间的函数，另一种是对象级别的插件开发，即给 jQuery对象添加方法。下面就两种函数的开发做详细的说明。 1 、类级别的插件开发类级别的插件开发最直接的理解就是给jQuer
Rome解析Rss 413277409 Rome解析Rss
import java.net.URL; import java.util.List; import org.junit.Test; import com.sun.syndication.feed.synd.SyndCategory; import com.sun.syndication.feed.synd.S
RSA加密解密无量加密解密 rsa
RSA加密解密代码代码有待整理 package com.tongbanjie.commons.util; import java.security.Key; import java.security.KeyFactory; import java.security.KeyPair; import java.security.KeyPairGenerat
linux 软件安装遇到的问题 aichenglong linux 遇到的问题 ftp
1 ftp配置中遇到的问题 500 OOPS: cannot change directory 出现该问题的原因:是SELinux安装机制的问题.只要disable SELinux就可以了修改方法:1 修改/etc/selinux/config 中SELINUX=disabled 2 source /etc
面试心得 alafqq 面试
最近面试了好几家公司。记录下；支付宝，面试我的人胖胖的，看着人挺好的；博彦外包的职位，面试失败；阿里金融，面试官人也挺和善，只不过我让他吐血了。。。由于印象比较深，记录下； 1，自我介绍 2，说下八种基本类型；（算上string。楼主才答了3种，哈哈，string其实不是基本类型，是引用类型） 3，什么是包装类，包装类的优点； 4，平时看过什么书？NND，什么书都没看过。。照样
java的多态性探讨百合不是茶 java
java的多态性是指main方法在调用属性的时候类可以对这一属性做出反应的情况 //package 1; class A{ public void test(){ System.out.println("A"); } } class D extends A{ public void test(){ S
网络编程基础篇之JavaScript-学习笔记 bijian1013 JavaScript
1.documentWrite <html> <head> <script language="JavaScript"> document.write("这是电脑网络学校"); document.close(); </script> </h
探索JUnit4扩展：深入Rule bijian1013 JUnit Rule 单元测试
本文将进一步探究Rule的应用，展示如何使用Rule来替代@BeforeClass，@AfterClass，@Before和@After的功能。在上一篇中提到，可以使用Rule替代现有的大部分Runner扩展，而且也不提倡对Runner中的withBefores()，withAfte
[CSS]CSS浮动十五条规则 bit1129 css
这些浮动规则，主要是参考CSS权威指南关于浮动规则的总结，然后添加一些简单的例子以验证和理解这些规则。 1. 所有的页面元素都可以浮动 2. 一个元素浮动后，会成为块级元素，比如<span>,a, strong等都会变成块级元素 3.一个元素左浮动，会向最近的块级父元素的左上角移动，直到浮动元素的左外边界碰到块级父元素的左内边界；如果这个块级父元素已经有浮动元素停靠了
【Kafka六】Kafka Producer和Consumer多Broker、多Partition场景 bit1129 partition
0.Kafka服务器配置 3个broker 1个topic，6个partition，副本因子是2 2个consumer，每个consumer三个线程并发读取 1. Producer package kafka.examples.multibrokers.producers; import java.util.Properties; import java.util.
zabbix_agentd.conf配置文件详解 ronin47 zabbix 配置文件
Aliaskey的别名，例如 Alias=ttlsa.userid:vfs.file.regexp[/etc/passwd,^ttlsa:.:([0-9]+),,,,\1]，或者ttlsa的用户ID。你可以使用key：vfs.file.regexp[/etc/passwd,^ttlsa:.: ([0-9]+),,,,\1]，也可以使用ttlsa.userid。备注: 别名不能重复，但是可以有多个
java--19.用矩阵求Fibonacci数列的第N项 bylijinnan fibonacci
参考了网上的思路，写了个Java版的： public class Fibonacci { final static int[] A={1,1,1,0}; public static void main(String[] args) { int n=7; for(int i=0;i<=n;i++){ int f=fibonac
Netty源码学习-LengthFieldBasedFrameDecoder bylijinnan java netty
先看看LengthFieldBasedFrameDecoder的官方API http://docs.jboss.org/netty/3.1/api/org/jboss/netty/handler/codec/frame/LengthFieldBasedFrameDecoder.html API举例说明了LengthFieldBasedFrameDecoder的解析机制，如下：实
AES加密解密 chicony 加密解密
AES加解密算法，使用Base64做转码以及辅助加密： package com.wintv.common; import javax.crypto.Cipher; import javax.crypto.spec.IvParameterSpec; import javax.crypto.spec.SecretKeySpec; import sun.misc.BASE64Decod
文件编码格式转换 ctrain 编码格式
package com.test; import java.io.File; import java.io.FileInputStream; import java.io.FileOutputStream; import java.io.IOException; import java.io.InputStream; import java.io.OutputStream;
mysql 在linux客户端插入数据中文乱码 daizj mysql 中文乱码
1、查看系统客户端，数据库，连接层的编码查看方法： http://daizj.iteye.com/blog/2174993 进入mysql，通过如下命令查看数据库编码方式： mysql> show variables like 'character_set_%'; +--------------------------+------
好代码是廉价的代码 dcj3sjt126com 程序员读书
长久以来我一直主张：好代码是廉价的代码。当我跟做开发的同事说出这话时，他们的第一反应是一种惊愕，然后是将近一个星期的嘲笑，把它当作一个笑话来讲。当他们走近看我的表情、知道我是认真的时，才收敛一点。当最初的惊愕消退后，他们会用一些这样的话来反驳： “好代码不廉价，好代码是采用经过数十年计算机科学研究和积累得出的最佳实践设计模式和方法论建立起来的精心制作的程序代码。” 我只
Android网络请求库——android-async-http dcj3sjt126com android
在iOS开发中有大名鼎鼎的ASIHttpRequest库，用来处理网络请求操作，今天要介绍的是一个在Android上同样强大的网络请求库android-async-http，目前非常火的应用Instagram和Pinterest的Android版就是用的这个网络请求库。这个网络请求库是基于Apache HttpClient库之上的一个异步网络请求处理库，网络处理均基于Android的非UI线程，通
ORACLE 复习笔记之SQL语句的优化 eksliang SQL优化 Oracle sql语句优化 SQL语句的优化
转载请出自出处：http://eksliang.iteye.com/blog/2097999 SQL语句的优化总结如下 sql语句的优化可以按照如下六个步骤进行：合理使用索引避免或者简化排序消除对大表的扫描避免复杂的通配符匹配调整子查询的性能 EXISTS和IN运算符下面我就按照上面这六个步骤分别进行总结：
浅析：Android 嵌套滑动机制（NestedScrolling） gg163 android 移动开发滑动机制嵌套
谷歌在发布安卓 Lollipop版本之后，为了更好的用户体验，Google为Android的滑动机制提供了NestedScrolling特性 NestedScrolling的特性可以体现在哪里呢？ 比如你使用了Toolbar，下面一个ScrollView，向上滚
使用hovertree菜单作为后台导航 hvt JavaScript jquery .net hovertree asp.net
hovertree是一个jquery菜单插件，官方网址：http://keleyi.com/jq/hovertree/ ，可以登录该网址体验效果。 0.1.3版本：http://keleyi.com/jq/hovertree/demo/demo.0.1.3.htm hovertree插件包含文件： http://keleyi.com/jq/hovertree/css
SVG 教程（二）矩形天梯梦 svg
SVG <rect> SVG Shapes SVG有一些预定义的形状元素，可被开发者使用和操作：矩形 <rect> 圆形 <circle> 椭圆 <ellipse> 线 <line> 折线 <polyline> 多边形 <polygon> 路径 <path>
一个简单的队列 luyulong java 数据结构队列
public class MyQueue { private long[] arr; private int front; private int end; // 有效数据的大小 private int elements; public MyQueue() { arr = new long[10]; elements = 0; front
基础数据结构和算法九：Binary Search Tree sunwinner Algorithm
A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all
项目出现的一些问题和体会 Steven-Walker DAO Web servlet
第一篇博客不知道要写点什么，就先来点近阶段的感悟吧。这几天学了servlet和数据库等知识，就参照老方的视频写了一个简单的增删改查的，完成了最简单的一些功能，使用了三层架构。 dao层完成的是对数据库具体的功能实现，service层调用了dao层的实现方法，具体对servlet提供支持。 &
高手问答：Java老A带你全面提升Java单兵作战能力！ ITeye管理员 java
本期特邀《Java特种兵》作者：谢宇，CSDN论坛ID: xieyuooo 针对JAVA问题给予大家解答，欢迎网友积极提问，与专家一起讨论! 作者简介：淘宝网资深Java工程师，CSDN超人气博主，人称“胖哥”。 CSDN博客地址： http://blog.csdn.net/xieyuooo 作者在进入大学前是一个不折不扣的计算机白痴，曾经被人笑话过不懂鼠标是什么，