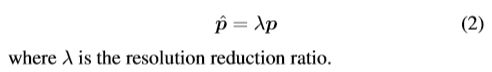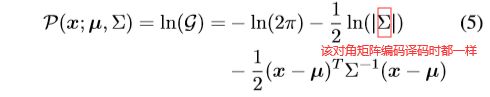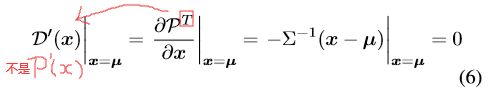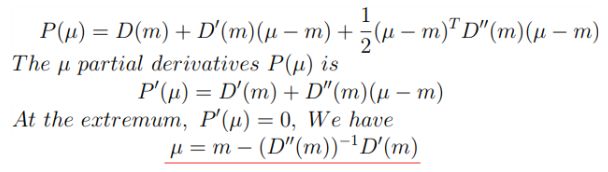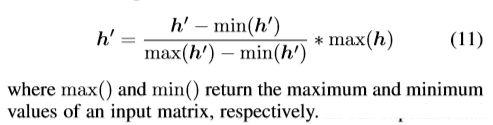人体姿态2019(八)Distribution-Aware Coordinate Representation for Human Pose Estimation
《Distribution-Aware Coordinate Representation for Human Pose Estimation》论文解读
- Abstract
- 1. Introduction
- 2. Methodology
-
- 2.1. Coordinate Decoding
-
- 2.1.1. The standard coordinate decoding method
- 2.1.2. The proposed coordinate decoding method
- 2.1.3. Heatmap distribution modulation
- 2.2. Coordinate Encoding
- Ref
原文:Distribution-Aware Coordinate Representation for Human Pose Estimation
收录:CVPR2019
代码:https://ilovepose.github.io/coco/
Abstract
热图 实际上是人体姿态估计中的标准坐标表示,但从未在文献中系统地研究过,本文将填补这个空白。将预测的热图译码为原始图像空间中的最终关节坐标这一过程对人体姿态估计的性能有着惊人的重要意义,而现有译码方法中广泛使用的 标准坐标译码方法 存在设计局限性,因此本文提出 可感知的分布式译码方法;同时,还改进了 标准坐标编码过程 (即将地面GT坐标转换为热图),结合这两者,本文提出 基于分布感知的关节点坐标表示方法 (DARK)。
1. Introduction
类似于图像分类的one-hot形式向量进行标签表示,姿态也需要标签来编码关节点坐标标签。实际的标准标签表示形式是坐标热图,它以2D高斯分布/内核为中心,以每个关节的标记坐标为中心生成(Tompson等人,2014)。 它是从坐标编码过程(从坐标到热图)来获得。
热图的特点是在GT值周围提供空间支持,不仅要考虑上下文线索,还要考虑目标位置固有的歧义性。 重要的是,与类标签平滑正则化的类似,这可以有效地减少模型在训练中的过拟合风险 (Szegedy等人,2016)。所以,最新的姿势模型 (Newell,Yang和Deng 2016; Xiao,Wu和Wei 2018; Sun等2019)基于热图来表示坐标。
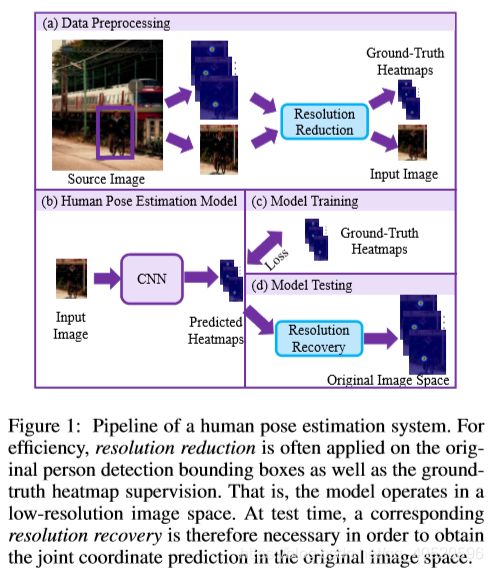
对于热图标签表示,一个主要障碍是,计算成本是输入图像分辨率的二次函数,从而使CNN模型无法处理通常的高分辨率原始图像数据。为了在计算上可以负担得起,一种标准策略(参见图1)是在将数据以人为姿态估计模型输入之前,使用数据预处理将所有任意较大的分辨率的包围框图像下采样到一个预先固定的小分辨率。在初始图像坐标空间中预测关节位置,为了预测关节在原始图像坐标空间中的位置,在进行热图预测之后,需要相应的分辨率恢复才能转换回原始坐标空间。最终预测被认为是具有最大响应的位置。我们将此过程称为 从热图到坐标的坐标译码。值得注意的是,在上述分辨率降低期间可能引入量化误差。为了缓解这个问题,在现有的坐标解码过程中,通常根据从最高响应到次高响应的方向进行手动移位操作(Newell,Yang和Deng,2016年)。
与现有的人体位姿估计研究相反,本文主要研究了包括编码和译码在内的关节点坐标表示问题。此外,我们认识到热图的分辨率是一个主要的障碍,它阻止使用较小的输入分辨率进行更快的模型推断。当输入分辨率从 256 × 192 256×192 256×192 降低到 128 × 96 128×96 128×96 时,虽然模型推理成本FLOPs 从 7.1 × 1 0 9 7.1×10^9 7.1×109 降低到 1.8 × 1 0 9 1.8×10^9 1.8×109,但 HRNet-W32 在COCO验证集上的模型性能从74.4%显著下降到66.9%。
2. Methodology
我们考虑了人体姿态估计中的坐标表示问题,包括编码和译码。目的是预测给定输入图像中的关节坐标。为此,我们需要学习从输入图像到输出坐标的回归模型,并且在模型 train 和 test 期间,热图 通常被用作坐标表示。具体来说,我们假设可以访问一组训练图像。为了促进模型学习,需要将标记的关节点坐标GT值编码为热图作为监督学习目标。在测试过程中,则将预测的热图译码为原始图像坐标空间中的坐标。
接下来各部分按以下顺序来介绍:
- 先对译码过程现有的标准方法局限性进行分析以及新方案的提出;
- 然后进一步讨论并解决编码过程的局限性;
- 最后将现有人体姿势估计模型与所提出方法进行集成。
2.1. Coordinate Decoding
具体来说,译码就是将预测的每个关节的热图转换为原始图像空间坐标的过程,若热图与原图像具有相同大小,那么就只需找到最大响应的位置作为预测的关节点坐标,这样简单又直观。但实际却不同,我们需要用sample-specific unconstrained factor(特定样本的无约束因子) λ ∈ R + \mathscr{\lambda }\in\mathcal{R}^{+} λ∈R+ 对热图进行上采样,这就涉及到亚像素的定位问题。
2.1.1. The standard coordinate decoding method
标准坐标译码方法就是根据模型性能进行经验设计。具体来说,先给训练好的模型输入热度图 h \mathcal{h} h,然后将最大响应点以及第二大响应点分别表示为 m \mathcal{m} m、 s \mathcal{s} s,则热图中的关节点位置被预测为:
这个式子可以解读为:热图中最终关节点位置就是从最大响应点出发,往第二大响应点方向偏移0.25像素所在的位置,在亚像素移动的目的是补偿图像分辨率下降采样的量化效应。
已知热图关节点位置,现在就要转化到原图中来,那么原图像的最终坐标则计算为:
这章节的理解:对于人体姿态估计方法有:回归关节点坐标、回归关节点热图。而热图的特点是在GT值周围提供空间支持,有效防止过拟合,是目前的主流。但在这个过程中有两个问题,且都会产生一定的误差:
- 由于编码需要将关节点坐标转换为关节点热图,会导致带小数坐标被转换到临近的整数位置;
- 译码时需将关节点热图转换回关节点坐标,这会导致得到的关节点是整数,与GT值产生误差。同时因为计算量的关系,热图通常会比输入图片缩小 n n n 倍,因此在恢复到原图时会将误差放大。标准坐标译码 方法是取最高峰位置 m \mathcal{m} m 为整数,将第二高峰位置 s \mathcal{s} s 作为小数补充。本文提出的改进方法则通过高斯估计,得到中心位置μ,获得了更好的效果。
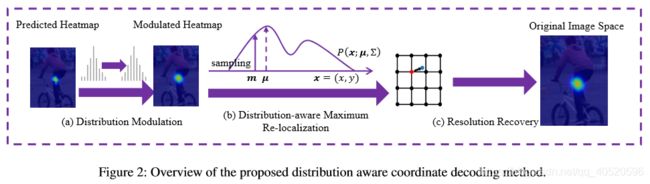
2.1.2. The proposed coordinate decoding method
改进的坐标译码方法则探索预测热图的分布结构,以推断潜在的最大响应位置。 这与依靠手动调整偏移量预测的标准坐标译码方法大不相同,之前方法几乎没有设计依据和理由。 具体来说,为了获得亚像素级的准确位置,假定预测的热图遵循2D高斯分布,与真实的热图相同。 因此预测的热图表示为:
对上式Eq.(3) 进行对数变换,则有:
由于均值处最大,那接下来的目标则是估计 µ µ µ。 作为分布的一个极值点,该位置的一阶导数满足以下条件:
然后使用 泰勒展开,在预测热图的最大响应 m m m 处用泰勒级数(直到二次项)来近似估计 P ( μ ) \mathcal{P(\mu )} P(μ)
推导:
∵ P ( x ; μ , Σ ) = − l n ( 2 π ) − 1 2 l n ( ∣ Σ ∣ ) − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) \because \mathcal{P(x;\mu ,\Sigma )} = -ln(2\pi ) - \frac{1}{2} ln(\left | \Sigma \right |) - \frac{1}{2}(x-\mu )^{T}\Sigma ^{-1}(x-\mu ) ∵P(x;μ,Σ)=−ln(2π)−21ln(∣Σ∣)−21(x−μ)TΣ−1(x−μ)
而 ∂ ( x T A x ) ∂ x = ( A + A T ) x \frac{\partial (x^{T}Ax)}{\partial x}=(A+A^{T})x ∂x∂(xTAx)=(A+AT)x
∴ ∂ P ∂ x = Σ − 1 ( μ − x ) \therefore \mathcal{\frac{\partial P}{\partial x}}= \Sigma ^{-1}(\mu -x) ∴∂x∂P=Σ−1(μ−x)
那么该导数的 s i z e size size 和 x x x 一样,但是由于泰勒展开的第二项应该是 P ′ ( m ) ( μ − m ) \mathcal{P'(m)(\mu -m)} P′(m)(μ−m),由于 ( μ − m ) (\mu -m) (μ−m) 的 s i z e size size 等于 x x x,所以不能相乘,若要相乘必须要转置,所以令 D ′ ( m ) = [ P ′ ( m ) ] T \mathcal{D'(m)=[P'(m)]}^{T} D′(m)=[P′(m)]T,第二项也就改为 D ′ ( m ) ( μ − m ) \mathcal{D'(m)(\mu -m)} D′(m)(μ−m)。
对于 μ \mu μ 的求解如下所示:
2.1.3. Heatmap distribution modulation
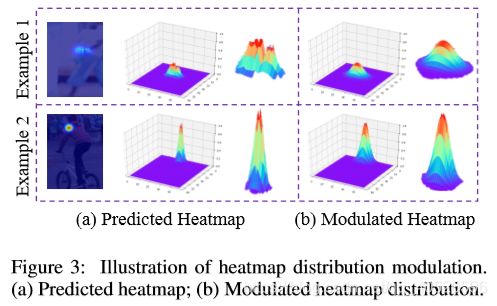
由于所提出的坐标译码方法是基于高斯分布假设的,但预测的热图通常在最大响应时呈现多个峰值,如Fig 3.(a) 所示,这可能会对译码方法的性能造成负面影响。为了解决这个问题,本文建议事先调整热图的分布,通过使用Gaussian kernel K K K,其方差和train数据一样,这样热图变化为:
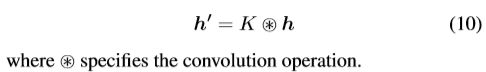
为了保证变化后热图的幅值与之前热图一致, h ′ h' h′ 还要如下变化:最后效果图如Fig 3.(b) 所示。
2.2. Coordinate Encoding
前面讨论译码的问题,其根本原因是分辨率降低导致的。作为一个类似的过程,坐标编码方法也有同样的局限性,标准坐标编码方法将原图像下采样到模型输入尺寸,那么GT值坐标如下变化:
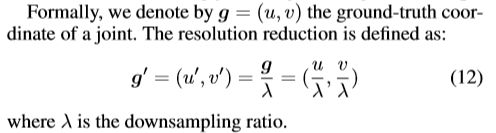
其中 quantise() 则是量化函数,常见的选择包括 floor、ceil 和 round,以量化后的坐标 g ′ ′ g'' g′′ 为中心的热图可以被合成为如下:
Ref
- Distribution-Aware Coordinate Representation for Human Pose Estimation估计关键点真实分布的均值位置
- Distribution-Aware Coordinate Representation for Human Pose Estimation 姿态估计 CVPR2019