二叉树的遍历-树-数据结构和算法(Java)

1 树的遍历方式

1.1 深度优先

事实上，深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.

那么对于树来说，"深度优先"有可以细分为前序遍历、中序遍历和后序遍历。

1.2 广度优先

BFS，其英文全称是Breadth First Search。 BFS并不使用经验法则算法。从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实验里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）

在树中中同样算法或者思想的遍历方式就是层序遍历。

2 二叉树的遍历方式

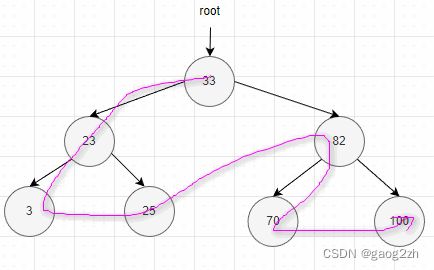
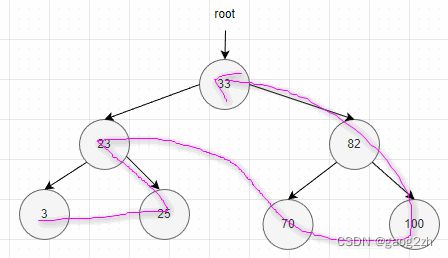
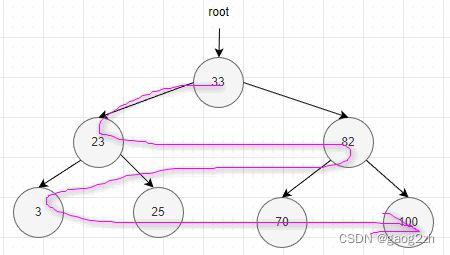
遍历都是从根结点开始，前序、中序和后序遍历，是指根结点相对于其左子树和右子树的访问顺序。实现方式为非递归实现，递归实现自行实现或者查阅相关文档。下面以一个二叉搜索树为例，来看看各种遍历方式结果。如下图2-1所示：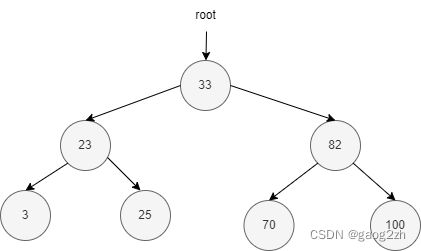

2.1 前序遍历

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。

非递归实现：

public Iterable<E> preTraversal() {
    Queue<E> q = new LinkQueue<>();
    Stack<TreeNode<E>> l = new Stack<>();
    l.push(root);
    while (!l.isEmpty()) {
        TreeNode<E> pop = l.pop();
        q.offer(pop.item);
        if (pop.right != null)
            l.push(pop.right);
        if (pop.left != null)
            l.push(pop.left);
    }

    return q;
}

前序遍历图示：

输出顺序：33 23 3 25 82 70 100

测试：更改BinarySearchTree迭代实现为前序遍历

Itr() {
    iterator = preTraversal().iterator();
}

public class TestTree {
    public static void main(String[] args) {
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        bst.add(33);
        bst.add(23);
        bst.add(82);
        bst.add(3);
        bst.add(25);
        bst.add(70);
        bst.add(100);

        System.out.println(bst);
    }
}
// 测试结果
[33,23,3,25,82,70,100]

2.2 中序遍历

中序遍历是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

非递归实现：

public Iterable<E> midTraversal() {
    Queue<E> q = new LinkQueue<>();

    Stack<TreeNode<E>> l = new Stack<>();
    TreeNode<E> current = root;

    while (current != null || !l.isEmpty()) {
        while (current != null) {
            l.push(current);
            current = current.left;
        }
        if (!l.isEmpty()) {
            current = l.pop();
            q.offer(current.item);
            current = current.right;
        }
    }

  return q;
}

中序遍历示意图如下2.2-1所示：

输出顺序：3 23 25 33 70 82 100

测试：

Itr() {
iterator = midTraversal().iterator();
}
// 测试代码同上
// 输出结果：
[3,23,25,33,70,82,100]

2.3 后序遍历

后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中，先左后右再根，即首先遍历左子树，然后遍历右子树，最后访问根结点。

非递归实现：

public Iterable<E> postTraversal() {
   Queue<E> q = new LinkQueue<>();

   Stack<TreeNode<E>> stack = new Stack<>();
   TreeNode<E> pre = root;
   TreeNode<E> current = root;
   while (current != null || !stack.isEmpty()) {
       while (current != null) {
           stack.push(current);
           current = current.left;
       }
       if (!stack.isEmpty()) {
           current = stack.peek().right;
           if (current == null || pre == current) {
               pre = stack.pop();
               q.offer(pre.item);
               current = null;
           }
       }
   }

   return q;
}

后序遍历示意图如下2.3-1所示：

输出顺序：3 25 23 70 100 82 33

测试：

Itr() {
iterator = postTraversal().iterator();
}
// 测试代码同上
// 测试结果
[3,25,23,70,100,82,33]

2.4 层序遍历

二叉树的层次遍历 ，顾名思义就是指从二叉树的第一层（根节点）开始，从上至下逐层遍历，在同一层中，则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中，按从顶层到底层的次序访问树中元素，在同一层中，从左到右进行访问。

非递归实现：

public Iterable<E> levelTraversal() {
    Queue<E> q = new LinkQueue<>();
    Queue<TreeNode<E>> l = new LinkQueue<>();
    l.offer(root);
    while (!l.isEmpty()) {
        TreeNode<E> pop = l.poll();
        q.offer(pop.item);
        if (pop.left != null)
            l.offer(pop.left);
        if (pop.right != null)
            l.offer(pop.right);
    }
    
    return q;
}

层序遍历示意图如下2.4-1所示：

输出顺序：33 23 82 3 25 70 100

测试：

Itr() {
iterator = levelTraversal().iterator();
}
// 测试代码同上
// 测试结果
[33,23,82,3,25,70,100]

3 后记

​ 如果小伙伴什么问题或者指教，欢迎交流。

❓QQ:806797785

⭐️源代码仓库地址：https://gitee.com/gaogzhen/algorithm

参考：

[1]百度百科.深度优先[EB/OL].

[2]百度百科.广度优先[EB/OL].

[3]百度百科.前序遍历[EB/OL].

[4]百度百科.中序遍历[EB/OL].

[5]百度百科.后序遍历[EB/OL].

[6]百度百科.层序遍历[EB/OL].

[7][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法：第4版[M].北京：人民邮电出版社，2012.10