关于模糊函数与距离多普勒耦合的理解

目录

一、引言

二、模糊函数

2.1 模糊函数的引入

2.2 模糊函数的性质

2.3 典型波形的模糊函数

2.3.1 简单矩形脉冲

2.3.2 LFM波

三、距离多普勒耦合

参考文献

---

一、引言

        匹配滤波(Matched Filtering)几乎是雷达信号处理中最重要的算法或者说是思想，其表达式虽然是比较唬人的卷积形式，但其过程无非是利用滑窗为对信号序列做内积，当窗信号的相位与被处理信号的相位完全补齐时(这里的对齐不一定指相位补齐后为零，而是指补齐后信号序列相位为不随时间变化的定值)，滤波器可在该处输出一峰值。

        这种思想在信号处理中很普遍：对于脉冲压缩(Pulse Compression)而言，滑窗信号为原信号的共轭信号，这也是要用发射信号的翻转共轭做滤波器系数的原因；对于动目标检测(Moving Target Detection)以及数字波束形成(Digital Beam Forming)，其原理其实是对信号序列做傅里叶变换，而该变换也可以理解为是一种匹配滤波，其窗信号为一定频率的单位复信号。可见，匹配滤波的思想对理解众多信号处理算法极其重要。

        在实际应用中，由于环境的复杂与未知，很多时候匹配滤波器会出现失配的情况，进而会带来增益损失或量侧误差。描述匹配滤波器失配情况的函数就是模糊函数(Ambiguity Function)。特别的，对于线性调频(Linear Frequency Modulated,LFM)波而言，在失配情况下会有距离多普勒耦合的现象。本文即对模糊函数以及距离多普勒耦合做以介绍以及记录下自己的理解。

二、模糊函数

2.1 模糊函数的引入

        对于动目标而言，雷达回波信号可表示为： 

        其中表示发射信号，表示多普勒频率，表示回波时延。由于多普勒频率未知，匹配滤波器构造为：

        因此匹配滤波输出为：

        令，上式可化为：

        不难看出，上式中分别表示匹配滤波器的时延失配量以及频率失配量，该式反映了存在这两种失配的情况下匹配滤波器的输出，因此基于上式可给出复模糊函数的定义式：

        对其求模可得模糊函数：

                 

        不难理解，模糊函数在时延维以及多普勒维的宽窄程度分别反映了这种波形的距离分辨率以及速度分辨率，这也是模糊函数最初设计的用途。加之模糊函数能描述匹配滤波器在失配情况下的输出情况，因此用来作为设计波形设计的参考。

        一般而言，匹配滤波器系数只是原发射信号的翻转共轭，不进行一定的频率调制，也即，因此此时有，下面的讨论即采用这样的情况。

2.2 模糊函数的性质

关于模糊有以下三个性质：

        ①若波形能量为，则有：

        不难理解该性质，因为当完全匹配时，匹配滤波输出的峰值就是波形能量。 

        ②能量守恒性质：

        ③对称性质：

         关于此三性质的证明可参文献[1]，这里就不赘述了。

2.3 典型波形的模糊函数

        考虑到篇幅受限以及笔者时间问题，以下不加推导的给出两种常用波形的模糊函数表达式以及图像，便于之后查阅翻看。

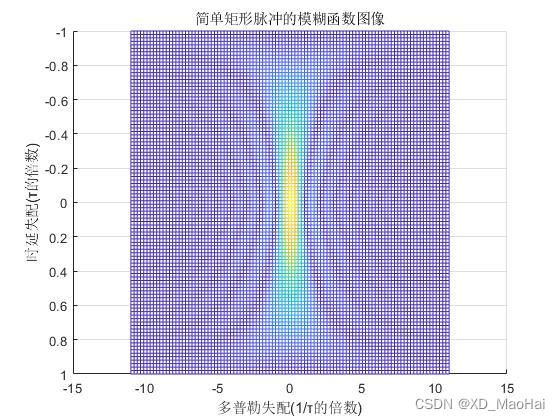
2.3.1 简单矩形脉冲

        假设一简单矩形脉信号为：

        其中表示脉冲宽度。其模糊函数为：

        其图像绘制如下：

        通过上图可知，当回波存在一定的多普勒频率而且不大时，进行匹配滤波后依旧会在预期峰值处()输出峰值，但峰值增益会有损失。但因为模糊函数在多普勒维下降很快，因此当多普勒频率增大时，匹配滤波输出在预期峰值处的值会快速下降，并逐渐会出现在时延轴的对称处而非在预期峰值处出现峰值的情况。

        虽然简单矩形脉冲有这种性质，对于一般的运动目标而言，其对回波信号造成的多普勒频移一般会比小很多，因此简单矩形脉冲信号可被归结为一种多普勒容许波形[1]。

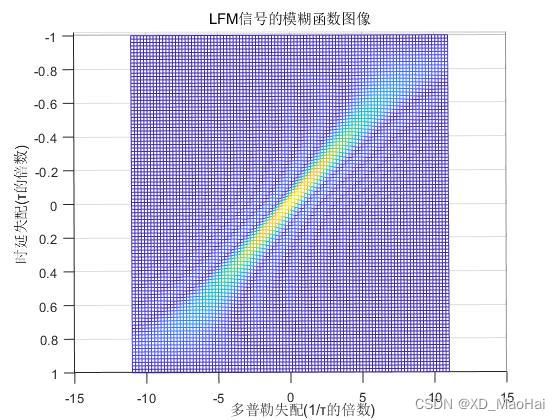
2.3.2 LFM波

         一般的LFM可表示为：

         其中为LFM信号的带宽。其模糊函数为：

         令时宽带宽积，可绘制图像如下：

 

        通过公式以及上面图像可知，LFM波的模糊函数是简单矩形脉冲模糊函数在多普勒维上发生倾斜和扭曲的结果。当回波不存在多普勒频移时，匹配滤波输出信号幅值为：

        可见最后匹配滤波器会在预期峰值处 ()输出峰值。但当回波存在多谱勒频率时，匹配滤波器在预期峰值处的值为：

        此时匹配滤波的输出不会在预期峰值处输出峰值，而是会偏离一定值，也即真实峰值输出的地方会偏离目标真实距离点，这就是LFM波所具有的距离多普勒耦合现象。这样的时延偏移量为：

       其中 表示距离频移量，可见该偏移量与多普勒频率是成正比的。下面将对该种现象作以仿真与理解。

三、距离多普勒耦合

        上面从LFM波模糊函数的公式与图像分析了距离多普勒耦合现象，为直观的看到多普勒频移给LFM波脉压测距的影响，首先给出以下脉冲压缩代码：

%% 波形参数
C = 3e8;                       % 光速
T = 50e-6;                     % 脉冲宽度
B = 2e6;                       % 频带宽度
K = B/T;                       % 调频斜率
Fs = 20*B;                     % 采样频率
Ts = 1/Fs;                     % 采样周期
fd = 0.1*B;                    % 回波多普勒频移
%% 回波窗参数
Rmin = 10000;Rmax = 150000;    % 测距范围
Rwid = Rmax-Rmin;              % 最大测距长度
Twid = 2*Rwid/C;               % 回波窗的长度
Nwid = ceil(Twid/Ts);          % 采样窗内的采样点数
R = [100e3];                   % 目标斜距
RCS = [1];                     % 雷达截面积
%% 产生回波    
t = linspace(2*Rmin/C,2*Rmax/C,Nwid);            % 回波窗                         
M = length(R);                                   % 目标的个数                                       
td = ones(M,1)*t-2*R'/C*ones(1,Nwid);            % 减去时延后的时间序列
Srt = RCS*(exp(1j*pi*K*td.^2+1j*2*pi*fd*td).*((td0));% 回波信号  
%% 脉冲压缩
Nchirp = ceil(T/Ts);               % 脉冲宽度内的采样点数
Nfft = 2^nextpow2(Nwid+Nchirp-1);  % 方便使用FFT算法，满足2的次方形式                                                
Srw = fft(Srt,Nfft);               % 回波做FFT
t0 = linspace(0,T,Nchirp);         % 脉冲宽度内时间序列
St = exp(1j*pi*K*t0.^2);           % 基带信号
Sw = conj(fft(St,Nfft));           % 滤波器系统函数
Sot = ifft(Srw.*Sw);               % 滤波   
Z = Sot(1:1+Nwid-1);               % 截取信号
%% 绘图
plot(t*C/2,abs(Z));
xlabel('距离/m');ylabel('幅值');
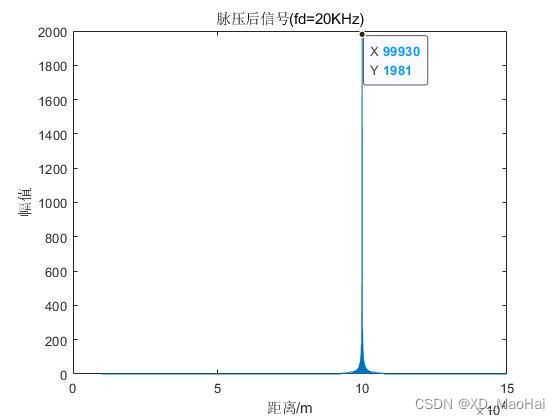
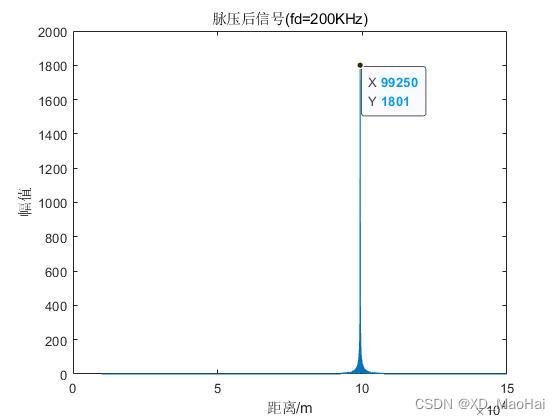
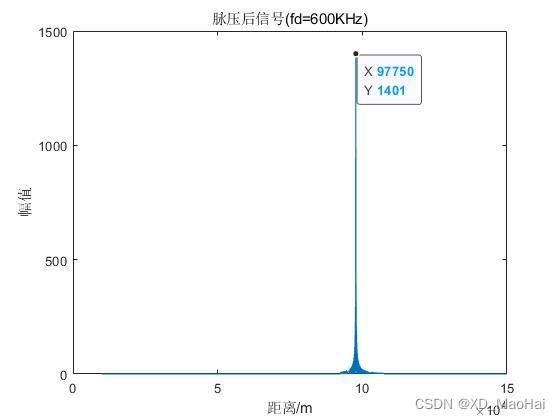
title(['脉压后信号(fd=',num2str(fd/1000),'KHz)']);

        改变代码中多普勒频移fd的数值可得到不同的测距结果(目标设定在100km处)如下：

        可见随着多普勒频移的增加，距离偏移量也会增大，并且两者之间的关系符合上面的计算式。此外，匹配峰值增益也会随着多普勒频移的增加而减少，其比例关系符合式。

        那么除公式和图像外，如何理解距离多普勒现象呢？还是回到匹配滤波的思想上来，正如文章开头所言，匹配滤波，或者说卷积的过程是利用滑窗为对信号序列做内积，当滑窗与信号序列的相位补齐时，滤波可在此处输出峰值。那么对于LFM的匹配滤波而言，滑窗到什么位置会与信号序列相位补齐呢？

        文章开头已经提到，匹配滤波的滑窗信号是发射信号的共轭，也即：

        其中表示滑窗从时间轴零点滑过的时间，当相位补齐时：

        对上式中的t做合并同类项并使其系数为0：

        可见利用相位对齐计算得到的结果与利用模糊函数计算得到的结果相同。这就说明了距离多普勒耦合产生的本质：当回波信号存在一个正值（负值）的多普勒频移时，滑窗会在距离回波时延提前（滞后）一段时间得到一定的频率补偿，补偿的这部分频率正好就是多普勒频率，以此来对信号相位作以补齐，从而在目标真实距离提前（滞后）一段距离输出了峰值，进而造成了测距误差。

       那么在实际应用中，这种多普勒频移带来的测距影响有多大呢？不妨令其与距离分辨率比较：

        对于厘米级雷达，脉冲宽度为，且以飞机为目标的情况下(100-300m/s)，由多普勒造成的测距误差也远小于距离分辨率，造成的误差影响不大，因此实际应用中常常忽略了距离多普勒耦合效应。但对于更高速运动目标（例如导弹）以及毫米级雷达，这种效应就不得不注意了。

        可以看到，与简单矩形脉冲相比，在一定多普勒频移的影响下，LFM波会有测距误差的，但这种效应有时也可以进行合理利用。由于LFM波的模糊函数具有“斜刀刃”的形状，在比较宽的多普勒频移范围内，匹配滤波峰值的衰减相较于简单脉冲的会小很多，因此对于具有较高多普勒频率的目标而言，LFM波往往具有更好的检测能力。而对于其存在的测距误差现象，可利用具有相反调频方向（正调频、负调频）的LFM进行测量，其测距平均值即为真实目标距离，从而消除了由多普勒带来的距离误差。

参考文献

[1] 理查兹, 邢孟道, 王彤,等. 雷达信号处理基础 : Fundamentals of radar signal processing[M]. 电子工业出版社, 2008. 

[2] 陈伯孝. 现代雷达系统分析与设计 : Mordern radar system analysis and design[M]. 西安电子科技大学出版社, 2012.