距离-多普勒谱(RD谱)之二:距离相关(匹配滤波)
一、前言
前文链接:https://blog.csdn.net/mddh_123/article/details/107891099
上一篇文章中,简单介绍了距离-多普勒谱的绘制方法,我们采用了“距离相关+多普勒变换”的方法实现RD谱的绘制。“距离相关+多普勒变换”方法仅在距离维进行了匹配滤波处理,计算量较小,是工程中主要采用的方法,但实际上该方法是绘制RD谱的“次优”方法。理论上的“最优”方法应为“模糊函数法”,即将相干积累时间内的参考信号经过一系列不同的时间延迟和多普勒频移,分别与目标回波进行相关。“模糊函数法”在距离维、多普勒维都通过循环迭代进行匹配滤波处理,计算量较大,工程中并不常用。
本篇文章主要针对匹配滤波的要点及注意事项进行阐述。
二、概念
匹配滤波的公式:
![]()
其中,h(t)是匹配滤波器冲激响应,s(t)是参考信号,x(t)是目标回波信号。
从上述公式,可得到以下结论:
1、匹配滤波是目标回波信号与匹配滤波器冲激响应的线性卷积,而匹配滤波器的冲激响应就是参考信号的“共轭、翻转”。因此,匹配滤波是目标回波与参考信号“共轭、翻转”的线性卷积。
2、匹配滤波是回波信号与参考信号共轭、翻转的线性卷积,那么就可以通过频域快速算法FFT实现。但是应注意的是,FFT对应的是“循环卷积”,需满足一定条件才能使得FFT快速算法结果与时域线性卷积结果相同,该条件将在后文介绍。
3、从公式最右侧的等式可知,匹配滤波又相当于目标回波信号与参考信号的互相关。(由于参考信号与目标回波信号基本一致,有些资料中也称为自相关。)
在MATLAB中,与上述三个结论分别对应的函数分别为conv、fft+ifft、xcorr。事实上,conv与xcorr在算法上等价,只差共轭、翻转两个步骤。
三、仿真分析
错误的打开方式: 如果采用下面的程序,结果很有可能让你很困惑!!!
clear all;
close all;
clc;
%% 参数
fs = 48e3; % 采样频率
Tp = (21 + 1/3) * 1e-3; % 脉冲宽度
Tr = 4 * Tp; % 脉冲重复周期
Nr = round(Tr * fs);
Np = round(Tp * fs);
fc = 5e3; % 载波频率
gamma = 500e3; % 调频斜率
%% 信号
t = (0:Np - 1) / fs; % 快时间
sref = [exp(1j * 2 * pi * (fc * t + 0.5 * gamma * t.^2)), zeros(1, Nr - Np)]; % 参考信号/发射信号
st = circshift(sref, 128);
figure;
plot(abs(fftshift(fft(st))));
figure;
plot(abs(st),'r');hold on;
%% 信道
st = awgn(st, 5);
plot(abs(st),'b');hold off;
%% 匹配滤波
% 法一:自相关法
out1 = xcorr(st, sref);
out1 = out1(Nr: end); % 前Nr - 1个数据与后Nr - 1个数据关于Nr对称,为了与后面长度一致,删去前面的重复数据
% 法二:卷积(时域)
out2 = conv(st, conj(fliplr(sref)));
out2 = out2(Nr: end); % 同理
% 法三:fft(频域)
out3 = ifft(fft(st) .* fft(conj(fliplr(sref))));
figure;
plot(abs(out1),'r');title('xcorr');
figure;
plot(abs(out2),'g');title('conv');
figure;
plot(abs(out3),'b');title('fft');
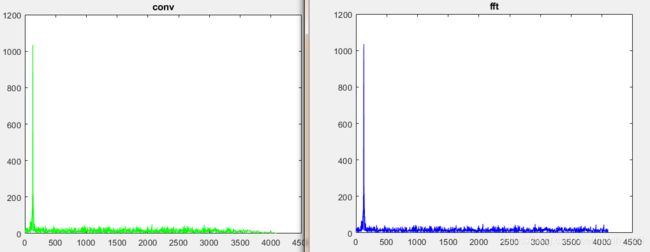
可以发现,采用上述程序时,fft方法的结果与conv方法的结果在3500-4000点时出现了不同,对于实际数据,该差距可能更明显。 我将在展示正确的代码之后,解释原因。
正确的方法: 如果理解下面这段程序,你将不再困惑~
clear all;
close all;
clc;
%% 参数
fs = 48e3; % 采样频率
Tp = (21 + 1/3) * 1e-3; % 脉冲宽度
Tr = 4 * Tp; % 脉冲重复周期
Nr = round(Tr * fs);
Np = round(Tp * fs);
fc = 5e3; % 载波频率
gamma = 500e3; % 调频斜率
%% 信号
t = (0:Np - 1) / fs; % 快时间
sref = [exp(1j * 2 * pi * (fc * t + 0.5 * gamma * t.^2)), zeros(1, Nr - Np)]; % 参考信号/发射信号
st = circshift(sref, 128);
figure;
plot(abs(fftshift(fft(st))));
figure;
plot(abs(st),'r');hold on;
%% 信道
st = awgn(st, 5);
plot(abs(st),'b');hold off;
%% 匹配滤波
% 法一:自相关法
out1 = xcorr(st, sref);
out1 = out1(Nr: end); % 前Nr - 1个数据与后Nr - 1个数据关于Nr对称,为了与后面长度一致,删去前面的重复数据
% 法二:卷积(时域)
out2 = conv(st, conj(fliplr(sref)));
out2 = out2(Nr: end); % 同理
% 法三:fft(频域)
out3 = ifft(fft(st, 2 * Nr - 1) .* fft(conj(fliplr(sref)), 2 * Nr - 1)); % 这里修改啦!!!!
out3 = out3(Nr:end); % 这里修改啦!!!!
figure;
plot(abs(out1),'r');title('xcorr');
figure;
plot(abs(out2),'g');title('conv');
figure;
plot(abs(out3),'b');title('fft');
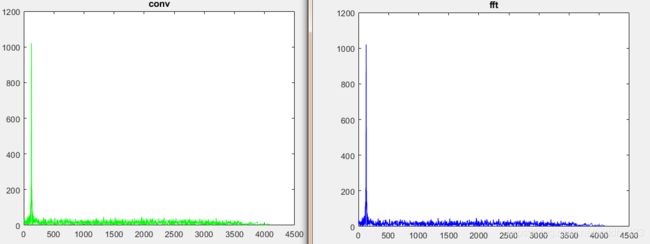
可以看到,在3500-4000点的误差已经完全被消除掉,这是因为满足了“循环卷积”等效计算“线性卷积”的条件,即FFT点数N>=N1 + N2 - 1。其中,N1、N2分别为两个信号删去左右两侧零值后的长度。
四、解释说明
事实上,MATLAB中conv函数计算的是两个序列的线性卷积,而fft则对应序列的循环卷积。循环卷积是将有限长的序列进行周期延拓,等效为周期序列,进行卷积计算的。网络上有许多人提问:“conv与fft结果为什么不同?”,这就是根本的原因。在满足下面的公式时,可以无误差地用循环卷积计算线性卷积:
![]()
其中,N1、N2分别为两个信号删去左右两侧零值后的长度。例如,x(t) = {0,0,-1,2,3,0},那么N1 = 3。
具体推导有时间再写文章说明【手动狗头】。
五、参考文献
[1]赵志欣. 高频外辐射源雷达新体制与信号处理若干关键技术研究[D].武汉大学,2013.