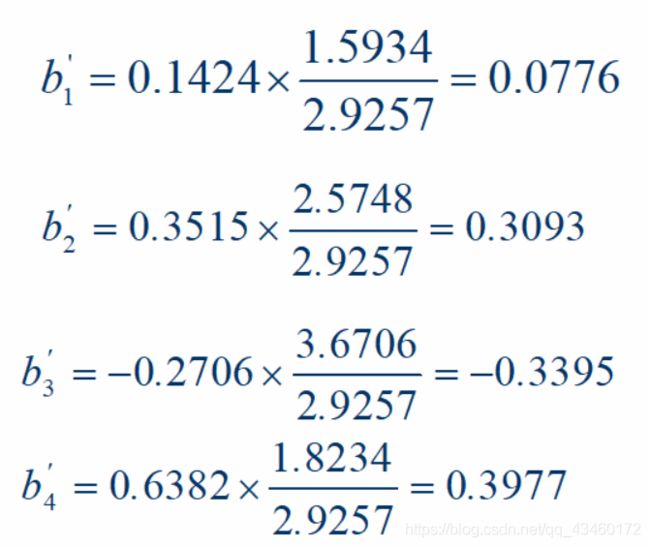【数学建模】多元线性回归分析
多元线性回归分析
概念
- 目的:作出以多个自变量估计因变量的多元线性回归方程。
- 资料:因变量为定量指标;自变量全部或大部分为定量指标,若有少量定性或等级指标需作转换。
- 用途:解释和预报。
- 意义:由于事物间的联系常常是多方面的,一个因变量的变化可能受到其它多个自变量的影响,如糖尿病人的血糖变化可能受胰岛素、糖化血红蛋白、血清总胆固醇、甘油三脂等多种生化指标的影响。
多元线性回归模型
一般形式
y = β 0 + β 1 X 1 + β 2 X 2 + . . . β n X n + e y = β_0+β_1X_1+β_2X_2+...β_nX_n+e y=β0+β1X1+β2X2+...βnXn+e
上式表示数据中应变量Y可以近似地表示为自变量 X 1 , X 2 . . . X m X_1,X_2...X_m X1,X2...Xm的线性函数。
β 0 β_0 β0为常数项, β 1 , β 2 , . . . β m β_1,β_2,...β_m β1,β2,...βm为偏回归系数,表示在其它自变量保持不变时, X j X_j Xj增加或减少一个单位时 Y Y Y的平均变化量, e e e是去除m个自变量对 Y Y Y影响后的随机误差(残差)。
一般步骤
- 求偏回归系数 b 0 , b 1 , b 2 . . . b m b_0,b_1,b_2...b_m b0,b1,b2...bm
- Y ^ = b 0 + b 1 X + b 2 X 2 + . . . b n X m \hat{Y} = b_0+b_1X+b_2X_2+...b_nX_m Y^=b0+b1X+b2X2+...bnXm
- 检验并评价回归方程及各自变量的作用大小
多元线性回归方程的建立
例:27名糖尿病人的血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白、空腹血糖的测量值列于下表中,试建立血糖与其它几项指标关系的多元线性回归方程。
| 序号i | 总胆固醇(mmol/L) X 1 X_1 X1 | 甘油三脂(mmol/L) X 2 X_2 X2 | 胰岛素(μU/ml) X 3 X_3 X3 | 糖化血红蛋白(%) X 4 X_4 X4 | 血糖(mmol/L) Y Y Y |
|---|---|---|---|---|---|
| 1 | 5.68 | 1.90 | 4.53 | 8.2 | 11.2 |
| 2 | 3.79 | 1.64 | 7.32 | 6.9 | 8.8 |
| 3 | 6.02 | 3.56 | 6.95 | 10.8 | 12.3 |
| 4 | 4.85 | 1.07 | 5.88 | 8.3 | 11.6 |
| 5 | 4.60 | 2.32 | 4.05 | 7.5 | 13.4 |
| 6 | 6.05 | 0.64 | 1.42 | 13.6 | 18.3 |
| 7 | 4.90 | 8.50 | 12.60 | 8.5 | 11.1 |
| 8 | 7.08 | 3.00 | 6.75 | 11.5 | 12.1 |
| 9 | 3.85 | 2.11 | 16.28 | 7.9 | 9.6 |
| 10 | 4.65 | 0.63 | 6.59 | 7.1 | 8.4 |
| 11 | 4.59 | 1.97 | 3.61 | 8.7 | 9.3 |
| 12 | 4.29 | 1.97 | 6.61 | 7.8 | 10.6 |
| 13 | 7.97 | 1.93 | 7.57 | 9.9 | 8.4 |
| 14 | 6.19 | 1.18 | 1.42 | 6.9 | 9.6 |
| 15 | 6.13 | 2.06 | 10.35 | 10.5 | 10.9 |
| 16 | 5.71 | 1.78 | 8.53 | 8.0 | 10.1 |
| 17 | 6.40 | 2.40 | 4.53 | 10.3 | 14.8 |
| 18 | 6.06 | 3.67 | 12.79 | 7.1 | 9.1 |
| 19 | 5.09 | 1.03 | 2.53 | 8.9 | 10.8 |
| 20 | 6.13 | 1.71 | 5.28 | 9.9 | 10.2 |
| 21 | 5.78 | 3.36 | 2.96 | 8.0 | 13.6 |
| 22 | 5.43 | 1.13 | 4.31 | 11.3 | 14.9 |
| 23 | 6.50 | 6.21 | 3.47 | 12.3 | 16.0 |
| 24 | 7.98 | 7.92 | 3.37 | 9.8 | 13.2 |
| 25 | 11.54 | 10.89 | 1.20 | 10.5 | 20.0 |
| 26 | 5.84 | 0.92 | 8.61 | 6.4 | 13.3 |
| 27 | 3.84 | 1.20 | 6.45 | 9.6 | 10.4 |
Q = ∑ ( Y − Y ^ ) 2 = ∑ [ Y − ( b 0 + b 1 X 1 + b 2 X 2 + ⋯ + b m X m ) ] 2 Q=\sum(Y-\hat{Y})^{2}=\sum\left[Y-\left(b_{0}+b_{1} X_{1}+b_{2} X_{2}+\cdots+b_{m} X_{m}\right)\right]^{2} Q=∑(Y−Y^)2=∑[Y−(b0+b1X1+b2X2+⋯+bmXm)]2
求偏导数↓
{ l 11 b 1 + l 12 b 2 + ⋯ + l 1 m b m = l 1 Y l 21 b 1 + l 22 b 2 + ⋯ + l 2 m b m = l 2 Y ⋯ ⋯ l m 1 b 1 + l m 2 b 2 + ⋯ + l m m b m = l m Y \left\{\begin{array}{l}{l_{11} b_{1}+l_{12} b_{2}+\cdots+l_{1 m} b_{m}=l_{1 Y}} \\ {l_{21} b_{1}+l_{22} b_{2}+\cdots+l_{2 m} b_{m}=l_{2 Y}} \\ {\cdots \cdots} \\ {l_{m 1} b_{1}+l_{m 2} b_{2}+\cdots+l_{m m} b_{m}=l_{m Y}}\end{array}\right.\\ ⎩⎪⎪⎨⎪⎪⎧l11b1+l12b2+⋯+l1mbm=l1Yl21b1+l22b2+⋯+l2mbm=l2Y⋯⋯lm1b1+lm2b2+⋯+lmmbm=lmY
b 0 = Y ‾ − ( b 1 X ‾ 1 + b 2 X ‾ 2 + ⋯ + b m X ‾ m ) b_{0}=\overline{Y}-\left(b_{1} \overline{X}_{1}+b_{2} \overline{X}_{2}+\cdots+b_{m} \overline{X}_{m}\right) b0=Y−(b1X1+b2X2+⋯+bmXm)
原理:最小二乘法
l i j = ∑ ( X i − X ‾ i ) ( X j − X ‾ j ) = ∑ X i X j − ∑ X i ∑ X j n , i , j = 1 , 2 , ⋯ , m l_{i j}=\sum\left(X_{i}-\overline{X}_{i}\right)\left(X_{j}-\overline{X}_{j}\right)=\sum X_{i} X_{j}-\frac{\sum X_{i} \sum X_{j}}{n}, i, j=1,2, \cdots, \mathrm{m} lij=∑(Xi−Xi)(Xj−Xj)=∑XiXj−n∑Xi∑Xj,i,j=1,2,⋯,m
l j T = ∑ ( X j − X ‾ j ) ( Y − Y ‾ ) = ∑ X j Y − ∑ X j ∑ Y n , j = 1 , 2 ⋯ , m l_{j T}=\sum\left(X_{j}-\overline{X}_{j}\right)(Y-\overline{Y})=\sum X_{j} Y-\frac{\sum X_{j} \sum Y}{n}, j=1,2 \cdots, m ljT=∑(Xj−Xj)(Y−Y)=∑XjY−n∑Xj∑Y,j=1,2⋯,m
Y ^ = 59433 + 0.1424 X 1 + 0.3515 X 2 − 0.2706 X 3 + 0.6382 X 4 \hat{Y}=59433+0.1424 X_{1}+0.3515 X_{2}-0.2706 X_{3}+0.6382 X_{4} Y^=59433+0.1424X1+0.3515X2−0.2706X3+0.6382X4
假设检验及其评价
一.对回归方程的显著性检验
1.方差分析法:
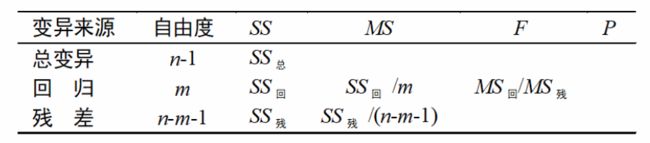
H 0 : β 1 = β 2 = ⋯ = β m = 0 H 1 : 各 β j ( j = 1 , 2 , . . . , m ) 不 全 为 0 a = 0.05 S S 总 = S S 回 + S S 残 F = S S 回 / m S S 残 / ( n − m − 1 ) = M S 回 M S 残 F ~ F ( m , n − m − 1 ) H_{0} : \beta_{1}=\beta_{2}=\cdots=\beta_{m}=0\\ H_1:各β_j(j=1,2,...,m)不全为0\\ a=0.05\\ SS_总=SS_回+SS_残\\ F=\frac{SS_回/m}{SS_残/(n-m-1)}=\frac{MS_回}{MS_残}\\ F~F(m,n-m-1)\\ H0:β1=β2=⋯=βm=0H1:各βj(j=1,2,...,m)不全为0a=0.05SS总=SS回+SS残F=SS残/(n−m−1)SS回/m=MS残MS回F~F(m,n−m−1)
表 多元线性回归方差分析表
表4 例题的方差分析表
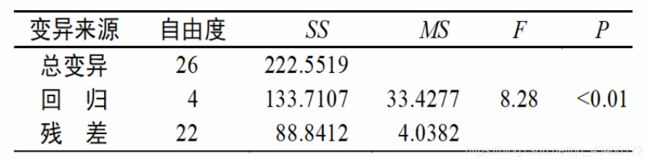
查 F 界 值 表 得 F 0.01 ( 4 , 22 ) = 4.31 , F > 4.41 , P < 0.01 在 a = 0.05 水 平 上 拒 绝 H 0 , 接 受 H 1 认 为 所 建 回 归 方 程 具 有 统 计 学 意 义 查F界值表得F_{0.01(4,22)}=4.31,F>4.41,P<0.01\\在a=0.05水平上拒绝H_0,接受H_1认为所建回归方程具有统计学意义 查F界值表得F0.01(4,22)=4.31,F>4.41,P<0.01在a=0.05水平上拒绝H0,接受H1认为所建回归方程具有统计学意义
2.决定系数 R2
R 2 = S S 回 S S 总 = 1 − S S 残 差 S S 总 R^2=\frac{SS_回}{SS_总}=1-\frac{SS_{残差}}{SS_总} R2=SS总SS回=1−SS总SS残差
0 ≤ R 2 ≤ 1 0≤R^2≤1 0≤R2≤1,说明自变量 X 1 , X 2 , . . . X m X_1,X_2,...X_m X1,X2,...Xm能够解释Y变化的百分比,其值愈接近于1,说明模型对数据的拟合程度较好
此例中, R 2 = 133.7107 222.5519 = 0.6008 R^2=\frac{133.7107}{222.5519}=0.6008 R2=222.5519133.7107=0.6008,说明血糖含量变异的60%可由总胆固醇、甘油三酯、胰岛素和糖化血红蛋白的变化来解释。
3.负相关系数
可用来度量应变量 Y Y Y与多个自变量间的线性相关程度,亦即观察值 Y Y Y与估计值 Y Y Y之间的相关程度。
计算公式: R = R 2 R=\sqrt{R^2} R=R2,本例 R = 0.6008 = 0.7751 R=\sqrt{0.6008}=0.7751 R=0.6008=0.7751
若m=1自变量,则有 R = ∣ r ∣ R=|r| R=∣r∣,r为简单相关系数。
二.方程中的每一个自变量对Y的影响(方差分析和决定系数检验整体)
1. 偏回归平方和
含义 回归方程中某一自变量 X j X_j Xj的偏回归平方和表示模型中含有其它m-1个自变量的条件下该自变量对Y的回归贡献,相当于从回归方程中剔除 X j X_j Xj后所引起的回归平方和的减少量,或在m-1个自变量的基础上新增加 X j X_j Xj引起的回归平方和的增加量。
F j = S S 回 ( X j ) / 1 S S 残 / ( n − m − 1 ) , v 1 = 1 , v 2 = n − m − 1 F_j=\frac{SS_回(X_j)/1}{SS_残/(n-m-1)},v_1=1,v_2=n-m-1 Fj=SS残/(n−m−1)SS回(Xj)/1,v1=1,v2=n−m−1
S S 回 ( X j ) SS_回(X_j) SS回(Xj)表示偏回归平方和,其值越大说明相应的自变量越重要。
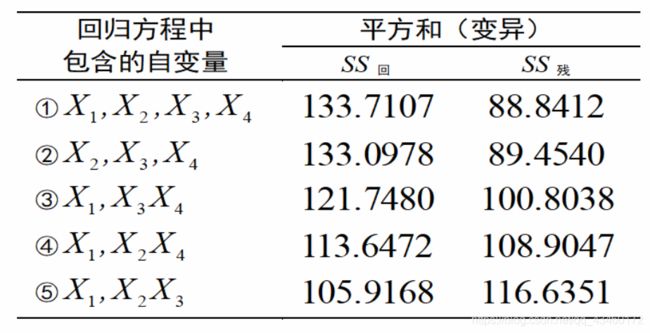
各自变量的偏回归平方和可以通过拟合包含不同自变量的回归方程计算得到
对例题1数据作回归分析的部分中间结果
作差得到 F 1 = ( ① − ② ) / 1 88.8412 / ( 27 − 4 − 1 ) . . . F_1=\frac{(①-②)/1}{88.8412/(27-4-1)}... F1=88.8412/(27−4−1)(①−②)/1...
(三)对回归系数的显著性检验(t检验)
含义 根据样本估计的结果对总体回归系数的有关假设进行检验
之所以对回归系数进行显著性检验,是因为回归方程的显著性检验只能检验所有回归系数是否同时与零有显著性差异,它不能保证回归方程中不包含不能较好解释说明因变量变化的自变量。
因此,可以通过回归系数显著性检验对每个回归系数进行考察。
回归参数显著性检验的基本步骤。
-
提出假设
-
计算回归系数的t统计量值
-
根据给定的显著水平α确定临界值,或者计算t值所对应的p值
-
作出判断
计算
结论
t 0.05 / 2.22 = 2.074 , t 4 > ∣ t 3 ∣ > 2.074 t_{0.05/2.22}=2.074,t_4>|t_3|>2.074 t0.05/2.22=2.074,t4>∣t3∣>2.074,P值均小于0.05,说明 b 3 b_3 b3和 b 4 b_4 b4有统计学意义,而 b 1 b_1 b1和 b 2 b_2 b2则没有统计学意义
标准化回归系数
变量标准化是将原始数据减去相应变量的均数,然后再除以该变量的标准差。
X ′ j = ( X j − X j ˉ ) S j X'j=\frac{(X_j-\bar{X_j})}{S_j} X′j=Sj(Xj−Xjˉ)
计算得到的回归方程称为标准化回归方程,相应的回归系数称为标准化回归系数。
b ’ j = b j l j j l Y Y = b j ( S j S Y ) b’_j=b_j\sqrt{\frac{l_{jj}}{l_{YY}}}=b_j(\frac{S_j}{S_Y}) b’j=bjlYYljj=bj(SYSj)
标准化回归系数没有单位,可以用来比较各个自变量对Y的影响强度
通常在有统计学意义的前提下,标准化回归系数的绝对值愈大说明相应自变量对Y的作用愈大。
一般回归系数有单位,用来解释各自变量对应变量的影响,表示在其它自变量保持不变时, 增加或减少一个单位时Y的平均变化量。
标准化回归系数无单位,用来比较各自变量对应变量的影响大小。
结果显示,对血糖影响大小的顺序依次为糖化血红蛋白 X 4 X_4 X4、胰岛素 X 3 X_3 X3、甘油三脂 X 2 X_2 X2和总胆固醇 X 1 X_{1} X1。
回归分析例题解析(SPSS操作流程)
题目
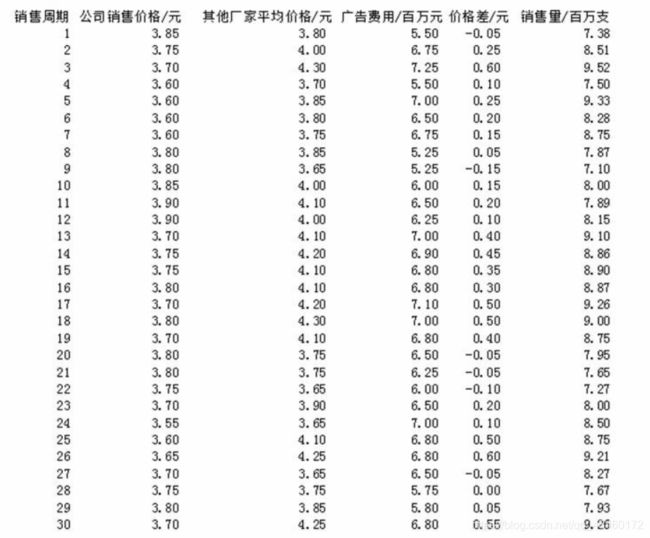
某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。为此销售部的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及其他厂家生产同类牙膏市场的平均销售价格,数据如下表所示:
表1 某大型牙膏制造企业销售数据
解题方法:
1、 找到问题关键词
如:“…找出公司生产的牙膏销售量与广告投入之间的关系,从而预测出在不同广告费用下的销售量。中带有“之间的关系”字样的,首先考虑要对样本数据散点图,然后考虑做相关性分析、均值比较、方差分析。发现带有“预测”字样的马上应想到要统计建模,最直接的就是采用回归分析。
(相关性分析主要通过计算相关系数判断变量之间是否具有相关性,均值比较和方差分析可以找到哪些因素对因变量有影响。)
2、问题分析
因消费者在购买牙膏时,更关心的是不同品牌之间的价格差,所以在研究各个因素对销售量的影响时,采用价格差代替公司的销售价格和其他厂家平均价格作为影响因素之一。因此,将价格差和广告费用作为自变量,牙膏的销售量作为因变量进行数据分析。
3、解题
(1)绘制散点图
由于要分析公司生产的牙膏销售量与销售价格、广告投入之间的关系,所以我们首先通过散点图来观察销售量与销售价格、与广告费用之间关系的散点图。
绘制散点图的操作方法
打开数据文件窗口的对话框,在菜单栏依次单击“图形”一“旧对话框”一“散点/点状”,选择“简单分布”,并分别将广告费用和价格差作为自变量选人X轴,销售量作为因变量选人Y轴,绘制散点图。
(2)曲线估计
从散点图来看,价格差与销售量呈现较明显的线性趋势,而广告费用和销售量呈现较明显的曲线趋势,但要判定两个变量更适合于哪个模型,则需要进行曲线估计。
曲线估计的操作方法
在菜单栏依次单击“分析”一“回归”一“曲线估计”,分别将广告费用和价格差选人自变量,销售量选人因变量,在模型选项组勾选“线性曲线”、“二次项曲线”和“立方曲线”三种曲线回归模型。
表2 广告费用与销售量曲线估计的模型
| 模型 | R | F | p | 常数 | bl | b2 | b3 |
|---|---|---|---|---|---|---|---|
| 线性 | 0.767 | 92.324 | 0.000 | 1.649 | 1.043 | ||
| 二次项 | 0.838 | 69.814 | 0.000 | 25.109 | -6.559 | 0.61 | |
| 立方 | 0.837 | 69.57 | 0.000 | 17.257 | -2.757 | 0.000 | 0.032 |
(SPSS结果中表格格式不为三线表,正文报告如果在word写其中表格应为三线表)
由表2可以看出,三个曲线估计的回归模型中,二次项曲线模型与立方曲线模型的拟合度显著优于线性模型,其中拟合度最好的是二次项曲线模型,其R 值为0.838,并且从F值来看,二次项曲线模型比立方曲线模型拟合的更显著。因此,选择二次项曲线模型最为理想,即
y = β 0 + β 1 x 1 + β 2 x 1 2 + ε y=β_0+β_1x_1+β_2x_1^2+ε y=β0+β1x1+β2x12+ε
其中x1为广告费用,y为销售量,ε为随机误差, β i β_i βi为回归系数( 0 ≤ i ≤ 2 0≤i≤2 0≤i≤2)
| 模型 | R | F | p | 常数 | bl | b2 | b3 |
|---|---|---|---|---|---|---|---|
| 线性 | 0.792 | 106.303 | 0.000 | 7.814 | 2.665 | ||
| 二次项 | 0.804 | 55.488 | 0.000 | 7.804 | 3.484 | -1.728 | |
| 立方 | 0.806 | 35.916 | 0.000 | 7.824 | 3.685 | -3.674 | 2.802 |
由表3可以看出,三个模型的拟合度基本相同,其中拟合度最好的是立方曲线模型,其次是二次项曲线模型,但立方曲线模型的参数比另外两种模型的参数多,更为复杂。若从F值来看,线性模型拟合的最为显著。但以上的结果还不足以作出判断,还需要对各模型系数作显著性检验。
重复上述操作,并且在曲线估计对话框勾选“显示ANOVE表格”。
表4 价格差与销售量的曲线估计的模型系数
| 模型 | 回归系数 | 标准差 | t | p | |
|---|---|---|---|---|---|
| 线性 | 价格差 | 2.665 | 0.258 | 10.31 | 0.000 |
| 常数 | 7.814 | 0.08 | 97.818 | 0.000 | |
| 价格差 | 3.484 | 0.667 | 5.226 | 0.000 | |
| 二次项 | 价格差**2 | -1.728 | 1.3O0 | -1.329 | 0.195 |
| 常数 | 7.804 | 0.079 | 98.607 | 0.000 | |
| 价格差 | 3.685 | 0.832 | 4.427 | 0.000 | |
| 立方 | 价格差**2 | -3.674 | 4.87 | -0.754 | 0.457 |
| 价格差**3 | 2.802 | 6.749 | 0.415 | 0.681 | |
| 常数 | 7.824 | 0.093 | 83.974 | 0.000 |
(表格不要跨页,如果上一页位置不够,则将表格加到下一页。加入空格或者Ctrl+回车都可以)
由表4可以看出,对三个模型系数进行显著性检验后,只有线性模型的系数均达到显著水平,而另外两种模型系数的P值至少有一个大于0.05。因此,选择线性模型最为理想,即
y = β 0 + β 1 + ε y=β_0+β_1+ε y=β0+β1+ε
其中 x2为价格差,y为销售量, ε ε ε为随机误差, β i β_i βi为回归系数( 0 ≤ i ≤ 2 0≤i≤2 0≤i≤2)。
(3) 模型建立与求解
模型一
由曲线估计知,价格差与销售量适合线性模型,而广告费用与销售量更适合二次项曲线模型。但因二次函数可以转化为线性函数,所以可将广告费用的平方作为一个新的自变量引入,从而采用多元线性回归分析,建立价格差、广告费用、广告费用的平方与牙膏的销售量的回归模型一,即
y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + ε y=β_0+β_1x_1+β_2x_2+β_3x_3+ε y=β0+β1x1+β2x2+β3x3+ε
其中 x1为广告费用,x2为广告费用,x3为广告费用的平方,y为销售量,ε为随机误差, β i β_i βi为回归系数( 0 ≤ i ≤ 3 0≤i≤3 0≤i≤3)。
多元回归分析之前,需引入新的变量。从“转换”菜单中,打开计算变量对话框,输入新的目标变量名,即广告费用的平方,然后在数字表达式中编辑函数,生成新的变量。接下来在“分析”菜单中,打开线性回归对话框,将广告费用、价格差和广告费用的平方同时选为自变量,将销售量选为因变量;单击“统计量”按钮,在弹出的对话框中勾选“置信区间”。
表5 回归模型一的模型
| 模型 | R | R2 | F | p |
|---|---|---|---|---|
| 广告费用、价格差和广告费用的平方 | 0.952 | 0.905 | 82.941 | 0.000 |
由表5可以看出,以广告费用、广告费用的平方和价格差共同作为自变量时,能显著预测销售量,其联合解释90.5%的变异量,因此模型一从整体上来看是可用的。
表6 回归模型一的模型系数
| 模型 | 回归系数 | t | p | 差分的95%置信区间 | |
|---|---|---|---|---|---|
| 下限 | 上限 | ||||
| 常数 | 17.324 | 3.071 | 0.005 | 5.728 | 28.921 |
| 价格差 | 1.307 | 4.305 | 0.000 | 0.683 | 1.931 |
| 广告费用 | -3.696 | -1.997 | 0.056 | -7.499 | 0.1O8 |
| 广告费用的平方 | 0.349 | 2.306 | 0.029 | 0.038 | 0.659 |
由表6可知,模型一的回归方程为 y = 17.324 + 1.307 x 1 − 3.696 x 2 + 0.349 x 3 + ε y=17.324+1.307x_1-3.696x_2+0.349x_3+ε y=17.324+1.307x1−3.696x2+0.349x3+ε。该模型显示,广告费用对销售量的影响不太显著,p值大于0.05,但广告费用的平方对销售量的影响是显著的,因此将广告费用作为回归变量仍保留在模型中。
模型二
尽管模型一从整体来看较为理想,但表5显示的置信区间[-7.499,0.108]包含零点,这说明广告费用对销售量的影响导致该模型不稳定,还需要进一步改进。模型一中,广告费用和价格差对于销售量的影响是相互独立的,而由现实经验可知,广告费用和价格差之间的交互作用也可能会影响牙膏的销售量。
考察变量间的交互作用,须先对变量作定性分析。
若变量均为分类变量,则采用方差分析来检验自变量对因变量的影响以及各自变量间的交互作用;若变量均为连续变量,则采用在回归方程中纳入变量的乘积项,通过检验其回归系数的显著性来判断变量间是否存在交互作用,如果回归系数为正,则变量间存在正交互作用,如果回归系数为负,则变量间存在负交互作用;若变量包含分类变量和连续变量,可将分类变量转换为虚拟变量后,当成连续变量再进行回归分析。
考虑到广告费用和价格差均为连续变量,因此采用在回归方程中纳入二者的乘积x4来代表广告费用和价格差的交互作用,记为“广告费用×价格差”。
具体操作如前,并在线性回归对话框中,单击“绘制”按钮,在弹出的对话框中将“*ZPRED”选人X轴,“*SRESID”选人Y轴,绘制标准化残差的散点图,同时勾选“直方图”,绘制标准化残差的频数分布图。
表7 回归模型二的模型
| 模型 | R | R2 | F | p |
|---|---|---|---|---|
| 广告费用、价格差、广告费用的平方、广告费用×价格差 | 0.96 | 0.921 | 72.777 | 0.000 |
表8 回归模型二的模型系数
| 模型 | 回归系数 | t | p | 差分的95%置信区间 | |
|---|---|---|---|---|---|
| 下限 | 上限 | ||||
| 常数 | 29.113 | 3.89 | 0.001 | 13.701 | 44.525 |
| 广告费用的平方 | 0.671 | 3.312 | 0.003 | 0.254 | 1.089 |
| 广告费用×价格差 | -1.478 | -2.215 | 0.036 | -2.852 | -0.104 |
| 广告费甩 | -7.608 | -3.081 | 0.005 | -12.693 | -2.523 |
| 价格差 | 11.134 | 2.504 | 0.019 | 1.978 | 20.291 |
由表7和表8可知,再引入广告费用×价格差后,联合解释92.1% 的变异量,较模型一有所提高,并且所有置信区间均不含零点,这说明模型二较模型一有所改进,更符合实际。模型二的回归方程为
y = 29.113 − 7.608 x 1 + 11.134 x 2 + 0.671 x 3 − 1.47 x 4 + ε y=29.113-7.608x_1+11.134x_2+0.671x_3-1.47x_4+ε y=29.113−7.608x1+11.134x2+0.671x3−1.47x4+ε
其中 x1为广告费用,x2为广告费用,x3为广告费用的平方,x4为广告费用×价格差,y为销售量, ε ε ε为随机误差。表7还显示,x4的回归系数估计值为-1.478,即广告费用和价格差存在负交互作用。当价格差较大时,可以较少地依赖广告投入的增加来提高销售量;当价格差较小时,则需要投入较大的广告费用来提高销售量。
分析残差直方图主要是分析其是否呈正态分布。在分析残差散点图时,要说明各点围绕残差等于0的直线上下是否随机分布,说明当前的回归模型对原始数据拟合情况如何(良好还是很差)。
补充资料:
python实现线性回归https://blog.csdn.net/weixin_40683253/article/details/81109129
SPSS傻瓜式实现线性回归https://blog.csdn.net/weixin_40683253/article/details/86736428
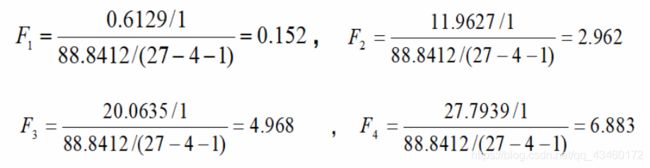

![[外链图片转存失败(img-Dpw4UEtH-1565186117279)(C:\Users\10310\Documents\我的坚果云\数学建模暑假培训\assets\1565183004754.png)]](http://img.e-com-net.com/image/info8/dec6817bda5e4e89afe08f660b283a68.jpg)