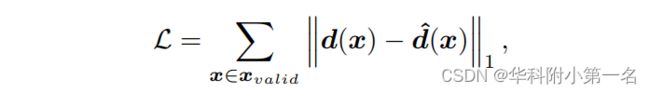【论文简述】Pyramid Multi-view Stereo Net with Self-adaptive View Aggregation(ECCV 2020)
一、论文简述
1. 第一作者:Hongwei Yi、Zizhuang Wei
2. 发表年份:2020
3. 发表期刊:ECCV
4. 关键词:MVS、深度学习、自适应视图聚合、多度量金字塔聚合
5. 探索动机:先前的网络没有充分学习和利用图像和多尺度的信息。不同视角的图像由于光照、相机几何参数、场景内容的可变性等原因,会提取到不同的特征;多尺度信息有利于提高三维重建的鲁棒性和完整性。
6. 工作目标:是否可以用新的结构充分利用各类信息,并实现更好的3D重建的完整性?
7. 核心思想:本文提出了一种有效且高效的金字塔多视图立体 (MVS) 网络,该网络具有自适应视图聚合,用于重建准确和完整的密集点云。具体提出了一个自适应的视图聚合模块(VA-MVSNet)来学习不同视图的图像在多个匹配体中的不同意义,模块通过自适应融合代价体,其中更好的元素匹配区域被增强,而不匹配的区域被抑制。为了进一步提高 3D 点云重建的鲁棒性和完整性,提出了一种新的方法(PVA-MVSNet),通过多度量约束聚合并行生成的多尺度金字塔深度图,以优化深度图。
8. 实验结果:该方法在DTU数据集上建立了一种新的先进方法,在完整性和整体质量上都有显著提高,并且具有较强的泛化能力,在Tanksa and Temples基准上的性能与先进方法相当。
9.论文&代码下载:
https://arxiv.org/abs/1912.03001v1
https://github.com/yhw-yhw/PVAMVSNet
二、实现过程
1. PVA-MVSNet概述
首先将多尺度金字塔图像输入至VA-MVSNet并行生成相应的金字塔深度图。然后,逐步用低分辨率层中更可靠的深度替换分辨率较高的深度图中不匹配的深度,从而得到改进的深度图。最后,通过对图像集估计的所有深度图进行滤波和融合,重建点云。
2. 学习部分
2.1. 自适应视图聚合
VA-MVSNet首先使用U-Net提取特征,从N个输入图像中提取具有较大感受野的特征图,为了提高计算效率,输出的特征图下采样4倍,具有32通道。然后使用类似于MVSNet中的可微单应性方法来形成多N个特征体。接着通过自适应视图聚合对不同视图的特征体进行编码,并通过3D U-Net进行正则化,回归深度图。
自适应元素的聚合模块:自适应元素聚合模块分为两种,一种是像素的聚合,一种是体素的聚合。
在聚合代价体时,在像素(高度和宽度)维度引入加权注意力,通过对应的权重图进行加权平均。具体公式如下:
首先计算各源视图特征体相对于参考视图的特征体的体残差,接着用PA-Net得到的权重进行聚合,其中权重通过下式计算:
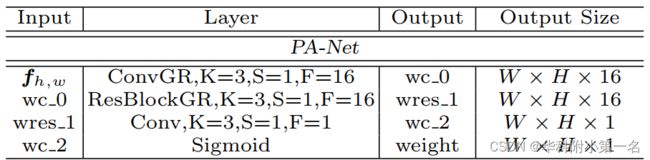
使用max pooling和avg pooling提取Vi深度维度的最高和平均代价匹配信息,CONCAT(·)表示在通道维度拼接操作。再输入PA-Net(由若干2DCNN和ResNet组成),生成2D加权注意力图。
PA-Net的详细信息
关于体素的聚合,在深度维度引入加权注意力,通过对应的权重图,对深度层假设d的每个体素进行加权平均。带有三维卷积滤波器的加权注意力图使用VA-Net直接学习,选择有用的代价信息。具体公式如下:
体素视图聚合模块
VA-Net的详细信息
2.2. 深度图、概率图估计
为了产生连续的深度估计,作者在输出概率volume P上使用 softmax 操作生成概率体P,并估计深度。
其中P(d)表示深度假设d的所有像素的估计概率,延续MVSNet,通过对概率体中最近的4个假设的和计算概率图来衡量估计质量。
2.3. 训练损失
使用了类似于MVSNet,采用平均绝对误差,定义为:
其中xvalid表示真实值中有效像素的集合,d(x)和d^(x)分别表示估计的深度图和真实值。
3. 非学习部分
3.1. 多度量金字塔深度聚合
到目前为止,网络VA-MVSNet生成了足够好的深度图来重建点云。为了进一步提高三维重建的鲁棒性和完整性,作者提出了一种新的多度量金字塔深度聚合结构(PVA-MVSNet)。输入图片被下采样后并行送入VA-MVSNet,得到几组对应的的不同大小的深度图和概率图。这些不同大小的深度图和概率图,经过文章中提出的多度量金字塔深度图聚合方法,来优化最终深度图的质量和点云的质量。
聚合方式如下图所示,将低分辨率的深度图中可信度高的部分来代替高分辨率深度图中可信度低的部分,用来代替重建过程中产生的错误匹配来达到优化深度图的效果。
从低分辨率到高分辨率改进策略如下:
光度一致性:使用概率图,低尺度深度(k+1)的概率值大于高阈值,而高尺度(k)概率值小于低阈值,对符合的位置用低尺度深度替换高尺度深度。空间一致性:通过光度一致性剔除不匹配误差后,对像素进行重投影,然后计算重投影的像素及深度的偏移。保留至少在三个相邻视图中满足以下几何约束的像素:
3.2. 滤波
- 光度一致性,滤掉置信度图中概率低于0.9的像素;
- 几何一致性,延续前面的空间一致性,像素应该至少在三个视图可见。
3.4. 深度图融合
4. 实验
4.1. 训练
使用DTU数据集训练VA-MVSNet,训练图像大小设置为W × H = 640 × 512,输入视图数N = 5,深度假设的采样范围为425mm至935mm,D = 192。通过PyTorch实现,在4张NVIDIA TITANX显卡训练,迭代16个epoch,batch size为4。Adam作为优化器,学习率设置为0.001,每1个epoch指数衰减0.9。
4.2. 测试
输入视图数N = 7,D = 192,自适应选择逆深度样本。我们在原始输入图像分辨率为1600 × 1184的DTU上评估方法。对于Tanks and Temples数据集,相机参数由OpenMVG计算,输入图像分辨率设置为1920 × 1056。我们使用相同的多度量约束参数,其中Elow = 0:5,Ehigh = 0:9, τ1 = 1和τ2 = 0:01。
4.3. 评价基准
DTU Dataset:accuracy 、completeness、overall score
结果:our PVA-MVSNet and VA-MVSNet establish a new state-of-the-art both in completeness and overall quality with a significant margin compared with all previous methods
Tanks and Temples Benchmark:f-score
结果:Our method outperforms Point-MVSNet [4] significantly with a higher 13% mean f-score, which is the best baseline on DTU dataset.
Our method generates more accurate and complete point clouds with higher precision and recall than the others, due to the enhanced accuracy from self-adaptive view aggregation and the increased completeness and robustness from our multi-metric pyramid depth map aggregation.
4.4. Ablation Studies
Self-adaptive View Aggregation:Specifically, the VoxelVA provides a 16:7% increase on accuracy, which is better than the PixelVA 14:1% due to the learning variance of the depth wise hypothesis. Besides, the VoxelVA has more parameters but less operations compared with PixelVA as denoted in Tab.
Number of Views:It demonstrates that our proposed self-adaptive view aggregation can well enhance the valid information in the good neighbor views and eliminate bad information in farrer views.
Multi-metric Pyramid Depth Aggregation:The K = 1 level pyramid image improves both accuracy and completeness with a big margin. A trade-off between accuracy and completeness is achieved by using more pyramid images k = 2 and k = 3, it leads to reconstructed 3D point cloud with better overall quality.
4.5 Running Time
All methods are tested on GeForce RTX 2080 Ti.VA-MVSNet runs fast at a speed of 0.91s / view, even if it runs with the biggest memory consumption. Unlike PointMVSNet, multiscale pyramid images can be processed independently in parallel. Therefore, with little extra time about 0.1s for multi-metric pyramid depth aggregation.