R语言实现决策树和朴素贝叶斯分类预测，并比较准确度（含数据集）

R语言实现决策树和朴素贝叶斯分类预测，并比较准确度（含数据集）

一开始用了《数据科学与大数据分析》（美国EMC教育服务集团）的书上的案例分析是否出去玩，后来发现只有10条训练数据，并且测试数据真值也不知道，故换了鸢尾花数据。
源数据链接：iris.data
提取码: frg4
如果打不开网盘请用这个地址，选iris.data右键保存：http://archive.ics.uci.edu/ml/machine-learning-databases/iris/
（感谢CSDN用户天使健的分享）
注意！！！这个下载后用txt打开也是data文件类型，不要读取错了

加载所需的包

rpart提供了决策树函数，plot绘图，klaR提供了朴素贝叶斯分类函数

library(rpart)
library(rpart.plot)
library(klaR)

读取数据并分集

注意文件路径，文件类型是data不是txt

#导入鸢尾花数据集
setwd("E:/Courses/专业课/大数据分析")    #调整默认的文件路径
data <- read.table("iris.data", header = FALSE, sep = ',')    #没有sep申明分隔符会导致全存进1个向量
names(data) <- c("Factor1","Factor2","Factor3","Factor4","Class")
print(data)

部分数据展示：

以0.8为划分标准，分出总量*0.8条训练集，其余为测试集。上述150条有120条训练数据，30条测试数据。随机产生。

set.seed(0)     #固定随机数，便于检查
train <- sample(nrow(data),0.8*nrow(data))    #随机选择150*0.2=30个数据为测试集，其余为训练集
print(train)
traindata <- data[train,]     #将抽样行赋给训练集
testdata <- data[-train,]     #将去掉抽样行的剩下的数据赋给测试集
print(traindata)
print(testdata)

随机产生了120个行号，剩下的用作测试

n <- length(testdata[,1])    #把测试集数据量赋给n，后面检验准确率用

构建决策树并计算准确率

#构建决策树并预测
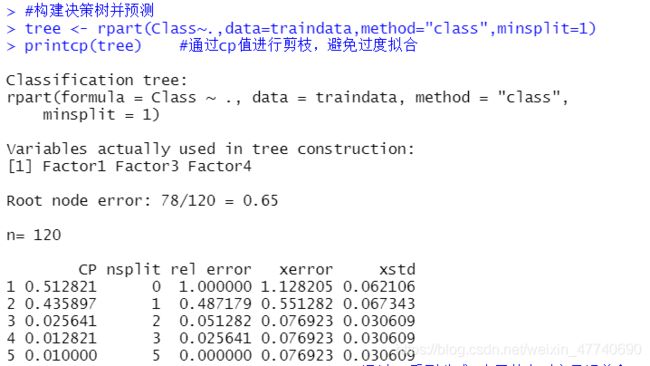
tree <- rpart(Class~.,data=traindata,method="class",minsplit=1)
printcp(tree)    #通过cp值进行剪枝，避免过度拟合

tree <- prune(tree, cp=0.025641)    #通过cp看到分成3个子节点时交叉误差和4一样
rpart.plot(tree,branch=0,type=4)

关于决策树的算法（ID3,CART)和rpart的各个参数，可以参考这篇blog
画出决策树的图：

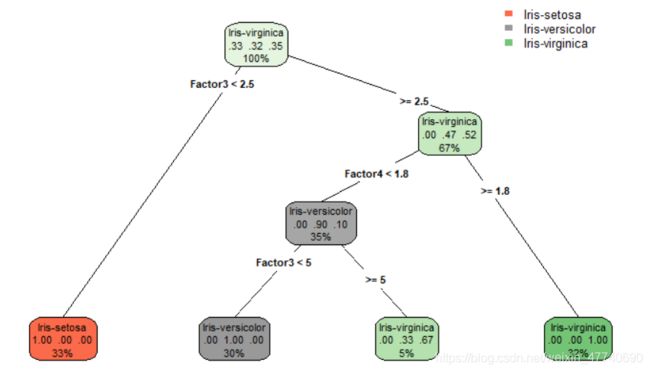
画好决策树后，用之前分出的testdata来预测：

predtree <- predict(tree,newdata=testdata,type="class")
testdata$Tree_Pre_Class <- predtree
a <- testdata$Tree_Pre_Class == testdata$Class
cnt1 <- sum(a[a=TRUE])
treerate <- cnt1/n
print(testdata)
print(a)
print(treerate)

为了便于观察，把预测结果写入testdata最后一列，a用来记录每一条预测的TRUE/FALSE值，cnt1统计了正确的个数，cnt1/n即为准确率。

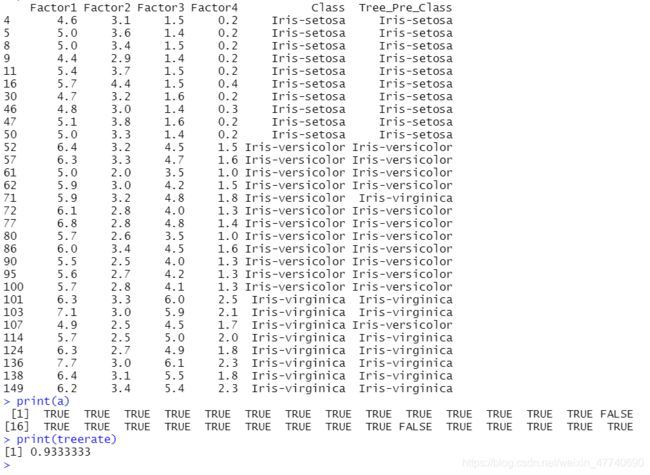
可见有2个预测错误，正确率28/30≈0.9333

朴素贝叶斯预测与准确率

#构建朴素贝叶斯算法并预测
traindata$Class <- as.factor(traindata$Class)    #将Class转化为函数可读取的因子，否则会报错
bayes <- NaiveBayes(Class~.,data=traindata)
bayes$apriori    #先验概率
bayes$tables    #每个变量的条件概率
#plot(bayes)

同样的思路来测试贝叶斯的预测准确度，不再赘述。只需注意相关函数的语法。

predbayes <- predict(bayes,testdata)
testdata$Bayes_Pre_Class = predbayes$class
b <- testdata$Bayes_Pre_Class == testdata$Class
cnt2 <- sum(b[b=TRUE])
bayesrate <- cnt2/n
print(testdata)
print(b)
print(bayesrate)

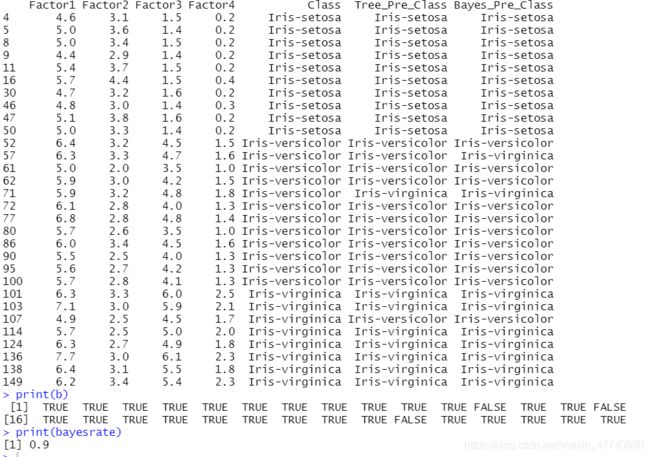
可以看出，在这个例子中贝叶斯有3个预测错误，准确度27/30=0.9，其准确度不如决策树模型。

完整代码如下

library(rpart)
library(rpart.plot)
library(klaR)


#导入鸢尾花数据集
setwd("E:/Courses/专业课/大数据分析")    #调整默认的文件路径
data <- read.table("iris.data", header = FALSE, sep = ',')
names(data) <- c("Factor1","Factor2","Factor3","Factor4","Class")
print(data)

set.seed(0)     #固定随机数，便于检查
train <- sample(nrow(data),0.8*nrow(data))    #随机选择150*0.2=30个数据为测试集，其余为训练集
print(train)
traindata <- data[train,]     #将抽样行赋给训练集
testdata <- data[-train,]     #将去掉抽样行的剩下的数据赋给测试集
print(traindata)
print(testdata)

n <- length(testdata[,1])    #把测试集数据量赋给n，后面检验准确率用


#构建决策树并预测
tree <- rpart(Class~.,data=traindata,method="class",minsplit=1)
printcp(tree)    #通过cp值进行剪枝，避免过度拟合
tree <- prune(tree, cp=0.025641)    #通过cp看到分成3个子节点时交叉误差和4一样
rpart.plot(tree,branch=0,type=4)

predtree <- predict(tree,newdata=testdata,type="class")
testdata$Tree_Pre_Class <- predtree
a <- testdata$Tree_Pre_Class == testdata$Class
cnt1 <- sum(a[a=TRUE])
treerate <- cnt1/n
print(testdata)
print(a)
print(treerate)


#构建朴素贝叶斯算法并预测
traindata$Class <- as.factor(traindata$Class)    #将Class转化为函数可读取的因子，否则会报错
bayes <- NaiveBayes(Class~.,data=traindata)
bayes$apriori    #先验概率
bayes$tables    #每个变量的条件概率
#plot(bayes)

predbayes <- predict(bayes,testdata)
testdata$Bayes_Pre_Class = predbayes$class
b <- testdata$Bayes_Pre_Class == testdata$Class
cnt2 <- sum(b[b=TRUE])
bayesrate <- cnt2/n
print(testdata)
print(b)
print(bayesrate)