K-Means 聚类算法 Python实现

聚类算法

        将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。“物以类聚，人以群分”，在自然科学和社会科学中，存在着大量的分类问题。聚类分析又称群分析，它是研究（样品或指标）分类问题的一种统计分析方法。聚类分析起源于分类学，但是聚类不等于分类。聚类与分类的不同在于，聚类所要求划分的类是未知的。聚类分析内容非常丰富，有系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。

（以上名词解释源自百度百科）

K-Means基本思想

• 初始化中心点
• 计算样本点与中心点之间的距离，将样本点归为最近的中心点的类中
• 根据类划分，计算新的样本中心点
• 重复操作直到中心点或类的归属不再发生变化

需要预设类的个数为K

---

代码解析

生成随机样本

import torch
import math
import matplotlib.pyplot as plt

# 利用torch的函数生成随机的样本点
X=torch.randn(2000)*100
y=torch.randn(2000)*100
# 一个长度为2000的向量，表示点的类别归属
C=torch.zeros(2000)

生成初始中心点

# 设置k-means的类别数
K = 5
CentPoint = []

for i in range(K):
    CentPoint.append([torch.randint(-100,100,(1,)).item(), 
                      torch.randint(-100,100,(1,)).item()])

K-Means算法

# 计算二维平面上点的距离
def dis(a,b):
    return math.sqrt((a[0]-b[0])*(a[0]-b[0])+(a[1]-b[1])*(a[1]-b[1]))

# K-Means
# 一般执行10次以内即可完成分类
for p in range(10):

    # NewPoint初始化为0
    NewPoint = [[0, 0] for i in range(K)]
    for i in range(len(X)):
        mDis=1e9
        mC=0
        for j in range(len(CentPoint)):
            cp=CentPoint[j]
            D = dis([X[i].item(), y[i].item()], cp)
            # print("distance:", D)
            if mDis>D:
                mDis=D
                mC=j
        C[i]=mC
        # print("mC",mC,C[i].item())
        NewPoint[mC][0]+=X[i].item()
        NewPoint[mC][1]+=y[i].item()

    # 更新中心点
    for i in range(K):
        CentPoint[i][0]=NewPoint[i][0]/2000
        CentPoint[i][1]=NewPoint[i][1]/2000

    # 输出中心点，观察变化过程
    print(CentPoint)

结果展示

cc=list(C)
# 按不同颜色来区分不同种类的点
for i in range(len(X)):
    if cc[i]==0:
        plt.plot(X[i].item(), y[i].item(), 'r.')
    elif cc[i]==1:
        plt.plot(X[i].item(), y[i].item(), 'g.')
    elif cc[i]==2:
        plt.plot(X[i].item(), y[i].item(), 'b.')
    elif cc[i]==3:
        plt.plot(X[i].item(), y[i].item(), color='pink', marker='.')
    elif cc[i]==4:
        plt.plot(X[i].item(), y[i].item(), color='orange', marker='.')

# 样本聚类的中心点
for CP in CentPoint:
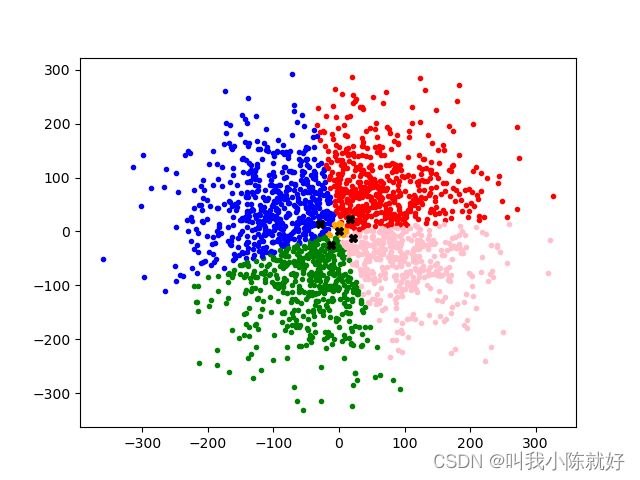
    plt.plot(CP[0], CP[1], color='black', marker='X')

可以观察出来，由于这组随机样本的生成是基于二维正态分布的，用K-Means来分析聚类，五个中心点的位置十分接近于二维正态分布的中心。

---

完整代码

import torch
import math
import matplotlib.pyplot as plt

def dis(a,b):
    return math.sqrt((a[0]-b[0])*(a[0]-b[0])+(a[1]-b[1])*(a[1]-b[1]))


X=torch.randn(2000)*100
y=torch.randn(2000)*100
C=torch.zeros(2000)

K = 5
CentPoint = []

for i in range(K):
    CentPoint.append([torch.randint(-100,100,(1,)).item(),
                      torch.randint(-100,100,(1,)).item()])

print(CentPoint)
for p in range(10):
    NewPoint = [[0, 0] for i in range(K)]
    for i in range(len(X)):
        mDis=1e9
        mC=0
        for j in range(len(CentPoint)):
            cp=CentPoint[j]
            D = dis([X[i].item(), y[i].item()], cp)
            if mDis>D:
                mDis=D
                mC=j
        C[i]=mC
        NewPoint[mC][0]+=X[i].item()
        NewPoint[mC][1]+=y[i].item()

    for i in range(K):
        CentPoint[i][0]=NewPoint[i][0]/2000
        CentPoint[i][1]=NewPoint[i][1]/2000
    print(CentPoint)

cc=list(C)
for i in range(len(X)):
    if cc[i]==0:
        plt.plot(X[i].item(), y[i].item(), 'r.')
    elif cc[i]==1:
        plt.plot(X[i].item(), y[i].item(), 'g.')
    elif cc[i]==2:
        plt.plot(X[i].item(), y[i].item(), 'b.')
    elif cc[i]==3:
        plt.plot(X[i].item(), y[i].item(), color='pink', marker='.')
    elif cc[i]==4:
        plt.plot(X[i].item(), y[i].item(), color='orange', marker='.')

for CP in CentPoint:
    plt.plot(CP[0], CP[1], color='black', marker='X')

plt.show()