Python-机器学习(三)-KMeans聚类算法
算法原理
- K-means算法是最常用的一种聚类算法。算法的输入为一个样本集(或者称为点集),通过该算法可以将样本进行聚类,具有相似特征的样本聚为一类。针对每个点,计算这个点距离所有中心点最近的那个中心点,然后将这个点归为这个中心点代表的簇。一次迭代结束之后,针对每个簇类,重新计算中心点,然后针对每个点,重新寻找距离自己最近的中心点。如此循环,直到前后两次迭代的簇类没有变化。
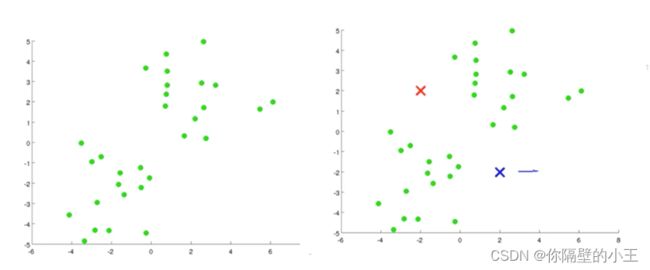
假设第一个图作为我们的原始数据集,设K=2,在图上随机选择两个K类所对应的类别质心,级途中的红色和蓝色的叉,计算样本中所有的点到这两个之心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别
如图3所示,经过计算样本中所有的点到两个质心的距离,我们得到了第一次迭代后的类别,此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示中心点已经发生了变化,56图重复上述过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。
- 基本的步骤为:
- step1:选定要聚类的类别数目k
- step2:针对每个样本点,找到距离其最近的中心点,距离同一中心点最近的点为一个类,这样完成了一次聚类。
- step3:针对每个类别中的样本点,计算这些样本点的中心点,当做该类的新的中心点,继续step2。
实际案例分析
from sklearn.cluster import KMeans
df= pd.read_csv('data.csv')
df.head()
df.info()
df.isnull().sum()可以看到,当前数据200行5列,包含用户ID,性别,年龄,年收入,支出没有空数据,将列名称设置为中文,方便查阅(emmmm 果然换成中文瞅着顺眼多了)
查看数据的分布情况
- 可以看到数据中年龄主要分布在20-40岁,女性居多,年收入大多数在90万以下,年支出在40-60万较多。
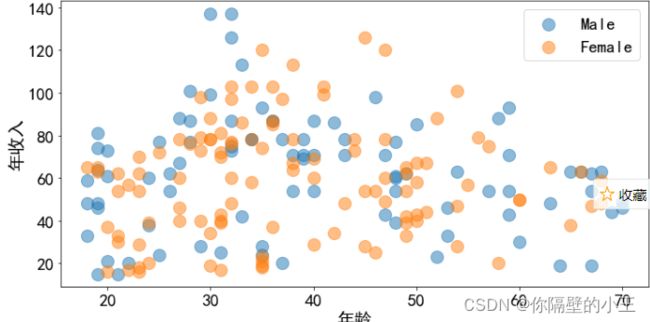
年龄与年收入之间的关系
查看年龄与年收入的关系,并对他们进行聚类分析
plt.figure(figsize=(12,6))
for gender in ['Male','Female']:
plt.scatter(x='年龄',y='年收入', data=df[df['性别']==gender],s=200,alpha=0.5,label=gender)
plt.xlabel('年龄')
plt.ylabel('年收入')
plt.legend()
plt.show() ## 寻找最佳K值
x1 = df[['年龄','支出']].values
inertia = []
for i in range(1,11):
km = KMeans(n_clusters=i)
km.fit(x1)
inertia.append(km.inertia_) #簇内的误差平方和
plt.figure(figsize=(12,6))
plt.plot(range(1,11),inertia)
plt.title("寻找最佳K值")
plt.xlabel('簇的数量')
plt.ylabel('簇内误差平方和')
plt.show()
##手肘原则根据手肘原则确定最佳K值为4
km = KMeans(n_clusters=4)
y_means = km.fit_predict(x1)
y_means
plt.figure(figsize=(12,6))
plt.scatter(x1[y_means==0,0],x1[y_means==0,1],s=200 )
plt.scatter(x1[y_means==1,0],x1[y_means==1,1],s=200 )
plt.scatter(x1[y_means==2,0],x1[y_means==2,1],s=200 )
plt.scatter(x1[y_means==3,0],x1[y_means==3,1],s=200 )
plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:,1],s=100, c='black', label='中心点')
plt.xlabel('年龄')
plt.ylabel('支出')
plt.legend()
plt.show()各年龄段支出、收入与支出之间的关系与年龄与年收入的关系类似,uu们可以自己试着分析一下看看自己掌握了没有!