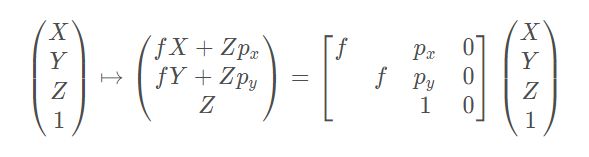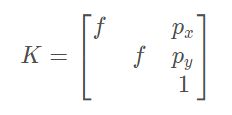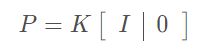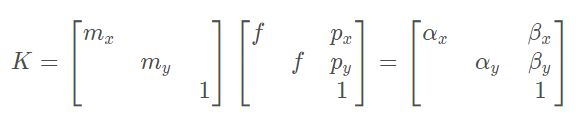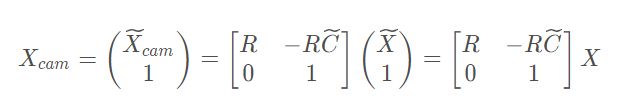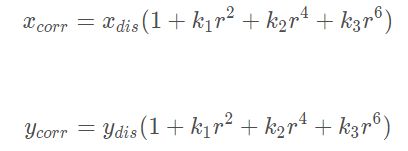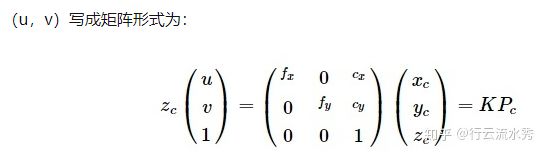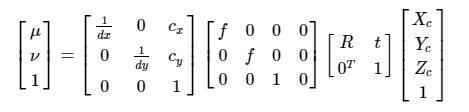OpenCV——相机标定(Camera calibration)
摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程,也就是求最终的投影矩阵 P PP 的过程。
所涉及的坐标系
- 世界坐标系(world coordinate system);
- 相机坐标系(camera coordinate system);
- 图像坐标系(image coordinate system);
标定的过程分为两个部分:
第一步是从世界坐标系转换为相机坐标系,这一步是三维点到三维点的转换,包括 R RR,t tt (相机外参)等参数;
第二部是从相机坐标系转为图像坐标系,这一步是三维点到二维点的转换,包括 K KK(相机内参)等参数;
相机坐标系转换到图像坐标系
如上图所示,是一个小孔成像的模型,其中:
 点表示
点表示camera centre,即相机的中心点,也是相机坐标系的中心点 轴表示
轴表示principal axis,即相机的主轴 点所在的平面表示
点所在的平面表示image plane,即相机的像平面,也就是图片坐标系所在的二维平面 点表示
点表示principal point,即主点,主轴与像平面相交的点 点到
点到 点的距离,也就是右边图中的
点的距离,也就是右边图中的 表示
表示focal length,即相机的焦距- 像平面上的
 和
和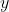 坐标轴是与相机坐标系上的
坐标轴是与相机坐标系上的 和
和 坐标轴互相平行的
坐标轴互相平行的 - 相机坐标系是以
 ,
, ,
, 三个轴组成的且原点在
三个轴组成的且原点在 点,度量值为米(m)
点,度量值为米(m) - 像平面坐标系是以
 两个轴组成的且原点在
两个轴组成的且原点在 点,度量值为米(m)
点,度量值为米(m) - 图像坐标系一般指图片相对坐标系,在这里可以认为和像平面坐标系在一个平面上,不过原点是在图片的角上,而且度量值为像素的个数(
pixel)
如果知道相机坐标系中的一个点 ![]() (现实三维世界中的点),在像平面坐标系对应的点是
(现实三维世界中的点),在像平面坐标系对应的点是![]() ,求相机坐标系转为像平面坐标系的转换,即点
,求相机坐标系转为像平面坐标系的转换,即点![]() 通过一定的转换变为点
通过一定的转换变为点![]() 。
。
通过图2我们可以发现
![]()
![]()
![]()
通过上面,可以把相机坐标系转换到像平面坐标系,但是像平面坐标系和图像坐标系虽然在同一个平面上,但是原点并不是同一个,而目标是要转换到图像坐标系下,所以还需要一步操作,如下图:
其中主点![]() 是像平面坐标系的原点,但在图像坐标系中的位置为(
是像平面坐标系的原点,但在图像坐标系中的位置为(![]() )
)
在这里图形坐标系的原点是图片的左下角,(![]() )
)![]() (
(![]() )
)
相当于在上面的基础上加了一个![]() 点坐标的偏移量,矩阵表示
点坐标的偏移量,矩阵表示
最后得到![]() 相机内参(Intrinsic parameters)
相机内参(Intrinsic parameters)
投影矩阵![]() (设旋转矩阵
(设旋转矩阵![]() 为单位矩阵
为单位矩阵![]() ,平移矩阵
,平移矩阵![]() 都为0)
都为0)
像素坐标
在图像坐标系中用的不是现实生活中的m来度量,而是用的 pixel 的个数,所以在上面转换到图像坐标系中还有个问题,就是坐标的表示还是m,并没有转换到像素坐标系统。
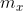 表示在水平方向
表示在水平方向1m的长度包含的像素的个数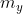 表示在竖直方向
表示在竖直方向1m的长度包含的像素的个数
通过上面可以得到一个像素点的大小(m度量)为
需要说明的是像素并不一定是一个正方形,有时候可能也是一个矩形,所以要分别指定。
更新上面相机内参![]()
一般来说,在使用相机内参K计算坐标系转换时,提供的都是已经变换后的值
一般见到的是![]() 分表对应相机内参
分表对应相机内参![]() ,对应上面矩阵
,对应上面矩阵![]() 分别对应
分别对应![]()
世界坐标系转到图像坐标系
如上图所示,从世界坐标系转换到相机坐标系是三维空间到三维空间的变换,一般来说需要一个平移操作和一个旋转操作就可以完成这个转换,用公式表示如下(可以理解为世界坐标系原点先平移到相机坐标系的位置然后在做一次坐标系旋转,使坐标轴对齐):
 表示旋转矩阵
表示旋转矩阵 表示
表示 点在世界坐标系中的位置
点在世界坐标系中的位置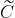 表示相机原点
表示相机原点 在世界坐标系中的位置
在世界坐标系中的位置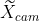 表示
表示 点在相机坐标系中的位置
点在相机坐标系中的位置
世界坐标转到相机坐标
根据上面的公式可以得到从一个三维点从世界坐标系转换到相机坐标的变换公式如下
世界坐标转到图像坐标
根据以上得到
得到投影矩阵![]()
其中
![]() 一般称为相机内参 (intrinsic parameters),描述了相机的内部参数,包括焦距
一般称为相机内参 (intrinsic parameters),描述了相机的内部参数,包括焦距![]() 、主点
、主点 ![]() 的位置、以及像素与真实环境的大小比例等,这个是固有属性。
的位置、以及像素与真实环境的大小比例等,这个是固有属性。![]() 和
和![]() 称为相机外参(extrinsic parameters),
称为相机外参(extrinsic parameters),![]() 是旋转矩阵,可以转换为三维的旋转向量,分别表示绕
是旋转矩阵,可以转换为三维的旋转向量,分别表示绕![]() 三个轴的旋转角度,
三个轴的旋转角度,![]() 目前就是一个平移向量,分别表示在
目前就是一个平移向量,分别表示在![]() 三个方向上的平移量。
三个方向上的平移量。
畸变参数(distortion parameters)
在几何光学和阴极射线管(CRT)显示中,畸变(distortion) 是对直线投影(rectilinear projection)的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变(optical aberration)。
径向畸变(Radial distortion)
径向畸变的效应有三种,一种是桶形畸变(barrel distortion),另一种是枕形畸变(pincushion distortion),还有一种是两种的结合叫做胡子畸变(mustache distortion),从图片中可以很容易看出区别,具体见下图(图片来自wikipedia):
![]()
径向畸变可以用如下公式修正:
切向畸变(tangential distortion)
切向畸变是由于透镜与成像平面不严格的平行,其可以用如下公式修正:
再次介绍
相机坐标系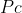 到像素坐标系
到像素坐标系
像素坐标系相比与相机坐标系进行了缩放和原点的平移(像素坐标系的原点一般为图像左上角),故像素坐标系![]() :
:
相机坐标系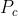 到世界坐标系
到世界坐标系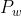
相机坐标系![]() 只是单个相机下的坐标,需要把所有相机拍的转换到同一个坐标系下,即世界坐标系
只是单个相机下的坐标,需要把所有相机拍的转换到同一个坐标系下,即世界坐标系![]() ,需要经过旋转和平移。
,需要经过旋转和平移。
![]()
其中![]() 是一个3*3的旋转矩阵,
是一个3*3的旋转矩阵,![]() 是一个3*1的平移矩阵。
是一个3*1的平移矩阵。
![]() 放一起成下面形式是一个4*4的矩阵,表示相机的外参(camera extrinsics)矩阵
放一起成下面形式是一个4*4的矩阵,表示相机的外参(camera extrinsics)矩阵
从像素坐标系到世界坐标系
![]() 为想x,y轴焦距
为想x,y轴焦距
关于![]() 焦距参见
焦距参见
https://www.cnblogs.com/zipeilu/p/6658177.html