PyTorch中的张量
文章目录
- PyTorch中的张量
-
- 1.张量的数据类型
- 2.张量的创建方式
- 3.张量的维度
- 4.张量的切片和索引
- 4.张量的运算
- 总结
PyTorch中的张量
1.张量的数据类型
深度学习框架的重要功能之一就是支持张量的定义和运算,PyTorch提供了专门的torch.Tensor类,在这个类中根据张量的格式和需要使用张量的设备,为张量开辟了不同的存储区域,对张量进行存储。
PyTorch中的张量一共支持9种数据类型,每种数据类型都对应CPU和GPU的两种子类型,如下表所示:
| 数据类型 | PyTorch类型 | CPU上的张量 | GPU上的张量 |
|---|---|---|---|
| 32位浮点数 | torch.float32/torch.float | torch.FloatTensor | torch.cuda.FloatTensor |
| 64位浮点数 | torch.float64/torch.double | torch.DoubleTensor | torch.cuda.DoubleTensor |
| 16位浮点数 | torch.float16/torch.half | torch.HalfTensor | torch.cuda.HalfTensor |
| 8位无符号整数 | torch.uint8 | torch.ByteTensor | torch.cuda.ByteTensor |
| 8位带符号整数 | torch.int8 | torch.CharTensor | torch.cuda.CharTensor |
| 16位带符号整数 | torch.int16/torch.short | torch.ShortTensor | torch.cuda.ShortTensor |
| 32位带符号整数 | torch.int32/torch.int | torch.IntTensor | torch.cuda.IntTensor |
| 64位带符号整数 | torch.int64/torch.long | torch.LongTensor | torch.cuda.LongTensor |
| 布尔型 | torch.bool | torch.BoolTensor | torch.cuda.BoolTensor |
下面来看实验:
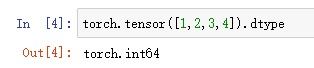
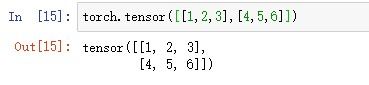
1.转换python列表为PyTorch张量

6.PyTorch默认浮点类型为32位单精度,numpy默认浮点类型为64位双精度
2.张量的创建方式
在PyTorch中创建张量主要有四种方式:
1.通过torch.tensor函数创建张量
这一部分内容如前文实验所述。
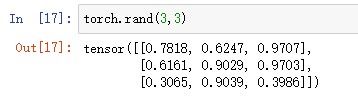
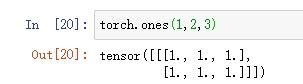
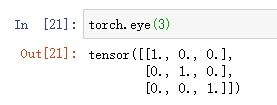
2.通过PyTorch内置函数创建张量
1.生成3×3的矩阵,矩阵元素服从[0,1]上的均匀分布

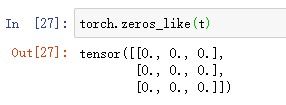
3.通过已知张量创建形状相同的张量
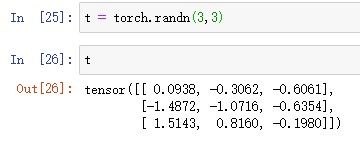
1.生成一个元素全为0的张量,形状和给定张量t相同

3.生成一个元素服从[0,1]均匀分布的张量,形状和给定张量t相同
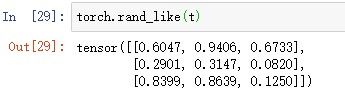
4.生成一个元素服从标准正态分布的张量,形状和给定张量t相同

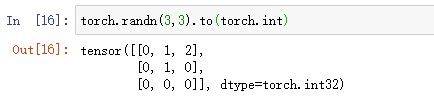
4.通过已知张量创建形状不同但数据类型相同的张量
这种方法在实际应用中很少用到,但在一定条件下,如写设备无关的代码有一定作用。
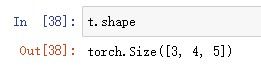
3.张量的维度
1.获取张量维度的数目和总元素数
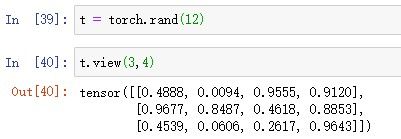
若view()的第一个参数为-1,则PyTorch会自动计算其具体的值。如view(-1,4)会自动计算为view(3,4)。
关于view方法:
view方法作用于原来的张量,传入改变新张量的形状,新张量的总元素数目和原来张量的元素数目相同。另外,假如新的张量有N维,可以指定其他N-1个维度的具体大小,留下一个指定为-1,这时PyTorch会自动计算那个维度的大小。view方法并不改变张量底层的数据,只是改变维度步长的信息,如果要重新生成一个新的张量,则需要调通contiguous方法。但是当引入transpose方法的时候,返回的新张量虽然还是共享底层的数据指针,但是维度和步长不再兼容。这时可以直接调用reshape方法,该方法会在形状信息不兼容的时候自动生成一个新的张量并自动复制原始张量的数据,相当于连续调用view方法和contiguous方法。
4.张量的切片和索引
1.对一个2×3×4的张量取0维1号,1维2号,2维3号的元素
4.张量的运算
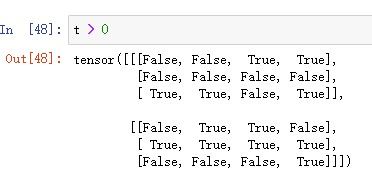
1.涉及单个张量的函数运算
1.张量的平方根
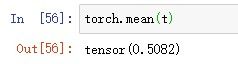
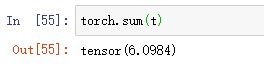
例如sqrt方法可以写成以_结尾,写成这种形式将会把这个张量的值复制到原始的张量中。同时例如求和、求平均等方法默认情况下会自动消除被计算的维度,如果要保留这些维度,需要设置参数keepdim=True,这样这个维度就会被保留为1。
2.涉及多个张量的函数运算
即张量之间逐个元素的四则运算,这里不再多讲。
3.张量的极值和排序
在进行深度学习的过程中,经常需要获取张量(沿着某个维度)的最大值和最小值,以及这些值所在的位置。如果只需要最大值或最小值的位置,可以使用argmax和argmin,通过传入具体要沿着哪个维度求最大值和最小值的位置,返回沿着该维度最大和最小值对应的序号是多少。如果既要获得最大和最小值的位置,又要获取具体的值,就需要使用max和min返回沿着该维度最大和最小值的位置以及对应最大最小值组成的元组。
1.返回沿着第0个维度极大值所在位置
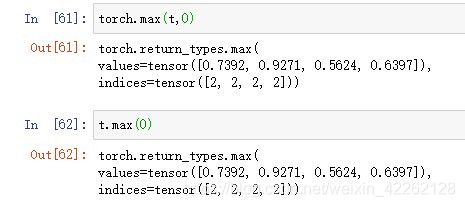
排序函数sort,默认顺序是从小到大,如果要从大到小需要设置参数descending=True。同样使传入具体需要进行排序的维度,返回的是排序完的张量,以及对应排序后的元素在原始张量中的位置。
1.沿着最后一个维度排序

4.矩阵的乘法和张量的缩并
除了四则运算外,由两个张量作为参数的操作还有矩阵乘法,即线性变换。

在深度学习中,经常用到Mini-batch的数据。因此一个矩阵实际上是一个Mini-batch的矩阵,即一个三维的张量。在这种情况下,如果对两个张量做矩阵乘法,一般情况下是沿着Mini-batch的方向分别对每个矩阵做乘法,最后把所有乘积的结果整合在一起。例如大小是b×m×k的张量和b×k×n的张量相乘,那么结果是b×m×n。

对于更大维度的张量的乘积,往往要决定各自张量元素乘积的结果需要沿着哪些维度求和,这个操作称为缩并。
对于爱因斯坦求和约定:

输入张量A,B得到输出结果C。这里把对应维度的下标分为三类:在A,B,C中都出现的,意味着这两个下标对应的一系列元素需要做两两乘积;如果仅在A,B中出现,但C中没有出现,意味着这两个下标对应的一系列元素要做乘积求和;在A,B中出现,C中仅出现一次且这两个指标对应的维度大小相对,意味着这两个维度之间元素按照位置做乘法。
torch.einsum函数在使用时需要传入两个张量下标对应的形状(以不同字母来区分)以及最后输出的张量的形状(用->连接)。
1.torch.stack函数通过传入的张量列表,同时指定并创建一个维度,把列表的张量沿着该维度堆叠起来,并返回堆叠以后的张量。(传入张量列表中所有张量的大小一致)。
将三个3×4的张量沿着最后一个维度堆叠,返回大小为3×4×3的张量

2.torch.cat通过传入张量列表指定某一个维度,吧列表中的张量沿着该维度堆叠起来,并返回堆叠以后的张量。与torch.stack的区别在于后者会新建一个维度,而cat中的维度是预先存在的,所有的张量会沿着这个维度堆叠。
将三个3×4的张量和一个3×2的张量沿着最后一个维度拼接得到一个3×14的张量

3.torch.split是执行前面叠加函数的反向操作,最后输出的是张量沿着某个维度分割后的列表。该函数传入三个参数,即被分割的张量、分割后维度的大小以及分割的维度。如果传入整数,则沿着传入维度分割成几段,每段沿着该维度的大小就是传入的整数;如果传入整数列表,则按照列表整数的大小来分割这个维度。
将一个3×6的张量沿着最后一个维度分割成3个张量
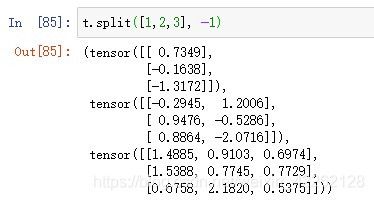
把张量沿着最后一个维度分割,分割大小为3,输出的张量大小均为3×3.

4.torch.chunk与split功能类似,区别在于前者传入的整数是分割的段数,输入张量在该维度的大小需要被分割的段数整除。
把张量沿着最后一个维度分割为三个张量,大小均为3×2.
6.张量的扩增和压缩
张量的扩增和压缩与张量大小等于1的维度有关。对一个张量来说,可以任意添加一个维度,该维度的大小为1,而不改变张量的数据。因为张量的大小等于所有维度大小的乘积,那些为1的维度不会改变张量的大小,这样就可以在张量中任意添加大小为1的维度。

7.张量的广播
如果两个不同维度张量之间做四则运算,这是不可行的。为了让其能够运算就需要把维度数目少的张量扩增到一致。举例来说,一个3×4×5的张量和3×5的张量做四则运算,先将3×5的张量展开成3×1×5,然后将3×1×5的张量沿着第二个维度复制4次,变成3×4×5的张量。
总结
以上就是关于PyTorch中的张量的一些基础知识,在深度学习的实践中会广泛运用。