Matlab数字图像处理 03 空域滤波(滤波器、线性滤波器、最大值滤波器、最小值滤波器、自适应中值滤波器、高斯低通滤波器、拉普拉斯算子锐化、钝化掩膜图像锐化))
第三章 空域滤波
-
- 3.1 线性滤波器
-
- 3.1.1 线性空域滤波器的计算流程
- 3.1.2 滤波核
- 3.1.3 相关运算与卷积运算
- 3.1.4 图像边界的处理
- 3.1.5 线性空域滤波器Matlab编程实现 ——imfilter( )、fspecia( )
- 3.2 统计排序滤波器
-
- 3.2.1 最大值滤波器、最小值滤波器
- 3.2.2 中值滤波器
- 3.2.3 自适应中值滤波器
- 3.2.4 中点滤波器
- 3.3 图像平滑
-
- 3.3.1 算术均值滤波器
- 3.3.2 高斯低通滤波器
- 3.4 图像锐化
-
- 3.4.1 基于拉普拉斯算子
- 3.4.2 钝化掩膜图像锐化
- 3.5 Matlab 常用的空域滤波函数
经典与现代滤波理论:
-
经典滤波器假定输人信号中的有用成分和希望去除的无用成分各自占有不同的频带,这样,当输入信号通过一个滤波器后,就可以将提取有用成分或去除无用成分。如果信号和噪声的频谱相互重叠,那么经典滤波器将无能为力。[根据傅里叶分析理论,任何满足一定条件的信号,都是由不同频率正弦信号线性组合而成。]
-
现代滤波器理论则从含有噪声的数据样本中,估计出信号的某些特征或信号本身。它把信号和噪声都视为随机信号,利用其统计特征导出一套最佳的估值算法,然后用硬件或软件予以实现,**维纳滤波器(Wienerfilter)、卡尔曼滤波器(Kalmanfilter)、自适应滤波器(Adaptivefilter)**便是这类滤波器的典型代表。本章介绍的统计排序非线性空域滤波器(Orderstatisticsfilter),也可归类为现代滤波器。
空域滤波与频域滤波: -
空域滤波(Spatial Filtering)按照一定的计算规则直接修改图像像素值。
-
频域滤波(Frequency Filtering)则是一种变换域滤波,它先对图像进行傅里叶变换,然后在变换域中对图像的频谱系数进行处理,再进行逆变换,最终获得滤波后的图像。
线性与非线性滤波 -
线性空域滤波器:滤波输出是该像素指定邻域内像素灰度值的线性组合。【均值滤波器、高斯低通滤波器】
例如, 3×3 均值滤波器,就是对该像素 3×3 邻域内9个像素灰度值,以相同的权值加权求和 -
非线性空域滤波器:滤波输出是该像素指定邻域内像素灰度值的非线性函数。
图像平滑与图像锐化 -
图像平滑:低通滤波器(low-passfilter)能保留信号的低频成分、去除或抑制高频成分,从而减弱图像像素灰度或颜色值的空间波动程度,使之变得平滑,导致图像模糊,故称图像平滑或模糊。
-
图像锐化:高通滤波器(high-passfilter)则保留信号的高频成分、去除或抑制低频成分,提取图像中的纹理细节;若将滤波结果叠加到原图像上,就可以强化图像边缘或轮廓,提高图像的清晰度,故称图像锐化。
![]()
3.1 线性滤波器
3.1.1 线性空域滤波器的计算流程
- 设计滤波器,确定滤波器作用区域的形状、尺寸和滤波器系数。
- 对图像中的每个像素(x,y),依据该像素的坐标(x,y)和滤波器作用区域的形状、尺寸,确定其邻域内参与运算的像素及其坐标。
- 将参与运算的像素灰度值与其对应滤波器系数相乘,并累加求和,得到像素(x,y)的滤波输出。
3.1.2 滤波核
线性空域滤波器作用区域的尺寸、形状,以及各像素的权值都可以用“滤波器系数数组” h 来描述,又称滤波模板、滤波掩模或滤波窗口、滤波器系数数组等。为便于编程,滤波器系数数组的行、列尺寸通常取奇数,以保证滤波模板在空间上为中心对称。因此,要定义一个m行、n列奇数尺寸的滤波模板,可令m=2a+1、n=2b+1,其中,a、b为非负整数,常用的滤波模板尺寸有3×3、5×5等。
模板中心:滤波器系数数组的中心位置元素称为模板中心,它是用于确定滤波器作用区域中像素与滤波器系数对应关系的“参考点”。
计算像素(x,y)滤波输出的一般步骤为:
(1) 将滤波模板h的中心平移到像素 (x,y) 上;
(2) 滤波器的每个系数 h(s,t) 与应像素的灰度值 f(x,y) 相乘,将乘积累加求和;
(3) 将累加和赋值给输出图像对应像素 g(x,y)
(4) 遍历图像 f(x,y) 的所有像素,重复步骤 (1~3)


3.1.3 相关运算与卷积运算
当滤波核的系数为中心对称时,即h(s,t)=h(-s,-t),线性空域滤波采用相关运算或卷积运算的结果是相同的。
MATLAB函数 imfilter 的输入参数filtering_mode用于指定在滤波过程中是使用相关('corr')还是卷积('conv'),输入参数无该选项时,默认采用相关('corr')。
3.1.4 图像边界的处理
在滤波过程中,会存在滤波器不能完全包含于图像中,位于图像外部的滤波器系数将没有像素与之对应,此时不能用 相关运算或者卷积运算,需要对图像边界进行处理。
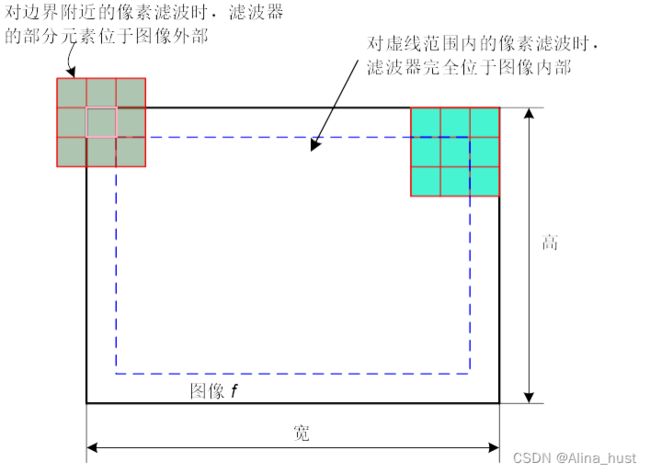
需要处理的图像边界部分可以定义为:滤波器的尺寸为 (2a+1) 行×(2b+1)列,需要对原图像上、下各扩展增加a行,左、右各扩展增加bl列。
常用方法有以下4种:
- 填充常值,图像边界外的像素用常值(例如,黑色0或灰色127)填充;
- 边界复制,将图像四个边界像素复制(replicate)到边界外;
- 边界镜像,将图像在四个边界处作镜像(symmetric)对称反射到边界外;
- 周期拓展,将图像在水平方向和垂直方向做周期性延拓(circular)
3.1.5 线性空域滤波器Matlab编程实现 ——imfilter( )、fspecia( )
函数 imfilter() 使用语法:

函数 fspecia( ) 使用语法:
函数 fspecial() 用来建立预定义的滤波器系数数组,其调用语法格式为:
h=fspecial(type)
h=fspecial(type,para)
- 返回值 h 是生成的滤波器系数数组;
- 输入参数 type为字符串变量,指定滤波模板类型,选项有
‘average’、‘disk’、‘gaussian’、‘laplacian’、‘log’、‘motion’、‘prewitt’、‘sobel’等。
参数type制定算子类型,parameters指定相应的参数,具体格式为:
type=‘average’,为均值滤波,参数为n,代表模版尺寸,用向量表示,默认值为[3,3]。
type= ‘gaussian’,为高斯低通滤波器,参数有两个,n表示模版尺寸,默认值为[3,3],sigma表示滤波器的标准差,单位为像素,默认值为0.5。
type= ‘laplacian’,为拉普拉斯算子,参数为alpha,用于控制拉普拉斯算子的形状,取值范围为[0,1],默认值为0.2。
type= ‘log’,为拉普拉斯高斯算子,参数有两个,n表示模版尺寸,默认值为[3,3],sigma为滤波器的标准差,单位为像素,默认值为0.5
type= ‘prewitt’,为prewitt算子,用于边缘增强,无参数。
type= ‘sobel’,为sobel算子,用于边缘提取,无参数。
type= ‘unsharp’,为对比度增强滤波器,参数alpha用于控制滤波器的形状,范围为[0,1],默认值为0.2。 - para指定类型滤波核相应的参数
示例:调用函数imfilter对图像平滑滤波
% 3.1 示例:调用函数imfilter对图像平滑滤波
clear;
clc;
f = imread('kafka.jpg');
h = fspecial('average',5);%创建一个5×5均值滤波器系数数组
g1 =imfilter(f,h);%用填充0扩展图像进行滤波(默认边界扩展方式)
g2 =imfilter(f,h,'replicate');%使用'replicate'选项扩展图像进行滤波
g3 = imfilter(f,h,'symmetric'); %边界处镜像
g4 = imfilter(f,h,'circular'); % 周期延拓
%显示处理结果
figure;
subplot(2,3,1);imshow(f);title('输入图像');
subplot(2,3,2);imshow(g1);title('填充0平滑滤波');
subplot(2,3,3);imshow(g2);title('扩展图像平滑滤波');
subplot(2,3,5);imshow(g3);title('边界处镜像平滑滤波');
subplot(2,3,6);imshow(g4);title('周期延拓平滑滤波');

数组扩展函数 padarray()

A: 输入图像; B:扩展后的图像

3.2 统计排序滤波器
非线性滤波器在某一像素处的滤波输出,是其邻域内像素值的非线性运算。统计排序空域滤波器是一类常用的非线性空域滤波器,如最大值滤波器。与线性空域滤波器另一个基本区别是,滤波模板的概念在非线性滤波处理中仍然存在,但通常用于规定参与运算的像素邻域的范围,如3×3最大值滤波器。

3.2.1 最大值滤波器、最小值滤波器
最大值滤波器适合 去除图像中黑色的噪声, 但同时会造成图像整体偏亮。

最小值滤波器适合去除图像中的白色噪点(高灰度值的脉冲噪声),与最大值滤波器相反,它会造成图像整体偏暗。
% 3.2 示例:最大值滤波器、最小值滤波器
clear;
clc;
i = imread('kafka.jpg');
f = rgb2gray(i);
%向图像中添加 椒噪声(peppernoise),噪声密度概率为0.1
%函数randperm(n,k)返回一个含k个不重复随机数的向量,元素在[1,n]范围内取值
pepper_ind = randperm(numel(f),floor(0.1*numel(f)));
%然后将图像中以该向量各元素值为线性序号的像素灰度值设为0,
fnp1 = f;
fnp1(pepper_ind) = 0; %加入黑噪点
%向图像中添加 盐噪声(saltnoise),噪声密度概率为0.1
fnp2 = f;
fnp2(pepper_ind) = 255; %加入白噪点
%3*3最大值滤波器去除“椒”噪声
g1=ordfilt2(fnp1,9,ones(3),'symmetric');
%3*3最小值滤波器去除“盐”噪声
g2=ordfilt2(fnp2,1,ones(3),'symmetric');
%显示处理结果
figure;
subplot(2,3,1);imshow(f);title('输入图像');
subplot(2,3,2);imshow(fnp1);title('加入椒噪声');
subplot(2,3,3);imshow(g1);title('最大值滤波');
subplot(2,3,4);imshow(f);title('输入图像');
subplot(2,3,5);imshow(fnp2);title('加入盐噪声');
subplot(2,3,6);imshow(g2);title('最小值滤波');
统计排序滤波函数 ordfilt2()
ordfilt2 :是一个2维统计排序滤波器,调用语法为:
其中,A为输入图像,B为输出图像。

-
ordfilt2 函数调用示例g = ordfilt2(f,1,ones(3)); % 3×3 最小值滤波 g = ordfilt2(f,5,ones(3)); % 3×3 中值滤波 g = ordfilt2(f,9,ones(3)); % 3×3 最大值滤波
图像噪声添加函数 imnoise()
3.2.2 中值滤波器
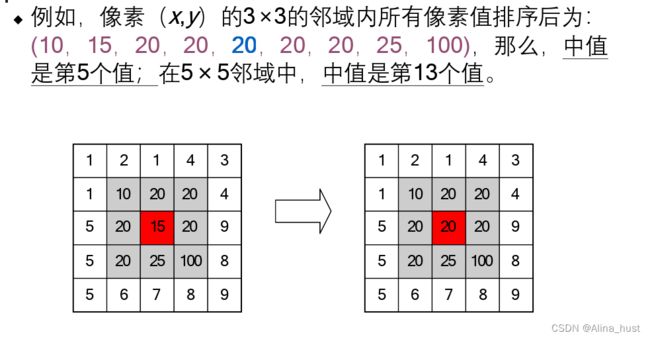
中值滤波器能有效去除图像脉冲噪声,即“椒盐”噪声。中值滤波器将像素(x,y)指定邻域 Sxy 内所有像素灰度值的中值,作为滤波器输出,即:

式中:Sxy为以像素(x,y)为中心的含有奇数个像素点的邻域窗口;一般取3×3、5×5等矩形邻域,也可以是线状、圆形、十字形或圆环形。
f(s,t) 为窗口Sxy内所有像素灰度值按大小排序后的一维数据序列。
% 3.2 示例:常规中值滤波与自适应中值滤波
clear;
clc;
i = imread('man.jpg');
f = rgb2gray(i);
%向图像中添加密度d=0.2的椒盐噪声
f1 = imnoise(f,'salt & pepper',0.2);
%采用常规3*3中值滤波器去噪
g1=medfilt2(f1,[3,3],'symmetric');
%采用常规5*5中值滤波器去噪
g2=medfilt2(f1,[5,5],'symmetric');
%采用最大邻域5*5自适应中值滤波器去噪
% g3=IMadpmedfilt2(f1,5);
%显示处理结果
figure;
subplot(2,3,1);imshow(f);title('输入图像');
subplot(2,3,2);imshow(f1);title('加入椒盐噪声');
subplot(2,3,4);imshow(g1);title('3*3中值滤波');
subplot(2,3,5);imshow(g2);title('5*5中值滤波');
%subplot(2,3,6);imshow(g3);title('最大邻域5*5自适应中值滤波');
中值滤波函数 medfilt2()
3.2.3 自适应中值滤波器
图像空域频率是指图像灰度或颜色在单位空间距离内周期性变化的次数。 算术均值滤波器又称滑动平均滤波器,是一种低通滤波器。令Sxy表示像素(x,y)的一个m×n矩形邻域,算术均值滤波就是计算邻域Sxy中所有像素灰度值的平均值,即: 二维高斯函数可表示为: 图像锐化(Image Sharpening)的本质,就是增强图像边缘的锐利程度。图像的高频分量与图像局部灰度值变化有关,图像锐化也就是增强图像的高频分量。 要注意的是,能够进行锐化处理的图像必须有较高的信噪比,否则,图像锐化后,信噪比会更低,因为锐化会提升噪声强度。一般是先去噪,再锐化操作 二维函数 f(x,y) 的拉普拉斯算子是指 沿 x 和 y 方向的二阶偏导数之和,作为各像素灰度值的局部变化量: 钝化掩膜(Unsharp Masking,USM)图像锐化技术,源于传统摄影中的暗室照片冲印技术,被很多图像处理软件采用,通常称USM滤镜(Unsharp Masking Filter)。

A步骤
先判断是否满足 Zmin
接下来考虑跳转到B之后的情况:判断中心点的像素值是否是噪声点,判断条件为 Zmin3.2.4 中点滤波器
3.3 图像平滑
边缘处像素灰度或颜色随空间的变化越锐利(变化快)、越剧烈(反差大),则边缘可辨程度越高,图像就越清晰。
反之,变化越圆钝(变化慢)、越柔和(反差小),则边缘可辨程度就越低,图像就越模糊。
3.3.1 算术均值滤波器

% 3.4 示例:滤波器尺寸对平滑效果的影响
clear;
clc;
i = imread('man.jpg');
f = rgb2gray(i);
%向图像中添加0均值,方差为0.01的高斯噪声
f1=imnoise(f,'gaussian',0,0.01);
%生成3*3均值滤波器
h=fspecial('average',3);
g1 = imfilter(f1,h,'replicate');%对原图像进行3*3平滑滤波
%生成9*9均值滤波器
h=fspecial('average',9);
g2 = imfilter(f1,h,'replicate');%对原图像进行9*9平滑滤波
%生成15*15均值滤波器
h=fspecial('average',15);
g3 = imfilter(f1,h,'replicate');%对原图像进行15*15平滑滤波
h=fspecial('average',35);
g4 = imfilter(f1,h,'replicate');%对原图像进行35*35平滑滤波
%显示处理结果
figure;
subplot(2,3,1);imshow(f);title('输入图像');
subplot(2,3,2);imshow(f1);title('加入高斯噪声');
subplot(2,3,3);imshow(g1);title('3*3平滑滤波');
subplot(2,3,4);imshow(g1);title('9*9平滑滤波');
subplot(2,3,5);imshow(g2);title('15*15平滑滤波');
subplot(2,3,6);imshow(g3);title('35*35平滑滤波');
3.3.2 高斯低通滤波器

示例:高斯低通滤波器图像平滑与边缘检测% 3.4.1 示例:高斯低通滤波器图像平滑与边缘检测
clear;
clc;
i = imread('man.jpg');
f = rgb2gray(i);
%采用edge函数,选择sobel算子对图像进行边缘检测
g=edge(f,'sobel');
%采用标准差sigma=1.5的高斯低通滤波器对图像平滑滤波
g1=imgaussfilt(f,1.5);
g2=edge(g1,'sobel');%对平滑后的图像进行边缘检测
%显示处理结果
figure;
subplot(2,2,1);imshow(f);title('输入图像');
subplot(2,2,2);imshow(g);title('sobel算子对图像进行边缘检测');
subplot(2,2,3);imshow(g1);title('sigma=1.5的高斯低通滤波器平滑滤波');
subplot(2,2,4);imshow(g2);title('对平滑后的图像进行边缘检测');
% 3.4.2 示例:对图像兴趣区域(ROI)进行平滑模糊
clear;
clc;
i = imread('man.jpg');
f = rgb2gray(i);
%鼠标交互获取兴趣区域ROI 运行后鼠标框出感兴趣区域,鼠标右键选择创建掩膜mask
mask=roipoly(f);
%采用20*20均值滤波器对指定区域平滑模糊
ha=fspecial('average',20);
g = roifilt2(ha,f,mask);
%显示处理结果
figure;
montage({f,g,mask},'Size',[1,3]);
title('输入图像| 对ROI平滑模糊结果 | ROI掩膜')
3.4 图像锐化
图像的清晰度与图像边缘和轮廓的锐利程度有关,边缘处像素的灰度或颜色随空间位置的变化越快、越剧烈,则图像就越清晰,细节的可辨程度就越高。
一般步骤:
3.4.1 基于拉普拉斯算子
Matab 中用滤波器创建函数 fspecial 创建拉普拉斯算子的滤波器调用格式
% 3.5 示例:用拉普拉斯算子进行图像锐化
clear;
clc;
i = imread('moon.jpg');
f = rgb2gray(i);
fd=double(f);%将原图像数据转换为double型
alpha=1.5;%定义锐化强度因子变量
%采用高斯低通滤波器对原图像平滑sigma=0.5
fs=imgaussfilt(fd,0.5);
%生成拉普拉斯滤波器系数数组
h=fspecial('laplacian',0);
%计算拉普拉斯二阶偏导图像
fL=imfilter(fs,h,'replicate');
g=fd-alpha*fL;%计算锐化图像
%对计算结果进行饱和处理
g(g<0)=0;g(g>255)=255;
%将锐化后的图像数据类型转换为uint8型
g = uint8(g);
%显示处理结果
figure;
subplot(1,3,1);imshow(f);title('输入图像');
subplot(1,3,2);imshow(g);title('拉普拉斯算子锐化结果');
subplot(1,3,3);imshow(fL,[]);title('拉普拉斯二阶偏导图像');
3.4.2 钝化掩膜图像锐化

示例:调用函数imsharpen进行钝化掩膜图像锐化% 3.5.1 示例:调用函数imsharpen进行钝化掩膜图像锐化
clear;
clc;
i = imread('moon.jpg');
f = rgb2gray(i);
%参数Radius-标准差,Amount-强度因子,Threshold-降噪阈值T
g=imsharpen(f,'Radius',1.5,'Amount',2,'Threshold',0.01);
%显示处理结果
figure;
montage({f,g});
title('输入图像(左)|锐化后的图像(右t)');
示例:钝化掩膜(USM)图像锐化的编程实现% 3.5.2 示例:钝化掩膜(USM)图像锐化的编程实现
clear;
clc;
i = imread('moon.jpg');
f = rgb2gray(i);
fd = double(f);
sigma=1.5;%定义高斯低通滤波器标准差,初始化为1.5
alpha=2;%定义锐化强度因子变量,并初始化为2
T=0.01;%定义降噪阈值,初始化为0.01
fs=imgaussfilt(fd,sigma);%对原图像进行高斯低通滤波平滑
fe=fd-fs;%用原图像减去模糊图像,差值即为边缘图像
%降低平缓区域中的锐化噪声,对边缘图像做阈值处理
fe(abs(fe)<T*255)=0;
%计算锐化图像,即原图像加上用alpha强度因子加权后的边缘图像
g=fd+alpha*fe;
%对计算结果进行饱和处理
g(g<0)=0;g(g>255)=255;
g=uint8(g);%将锐化后的图像数据类型转换为uint8型
%显示处理结果
figure;
subplot(1,3,1);imshow(f);title('输入图像');
subplot(1,3,2);imshow(g);title('USM 锐化结果');
subplot(1,3,3);imshow(fe,[]);title('USM 得到的边缘图像');
3.5 Matlab 常用的空域滤波函数







