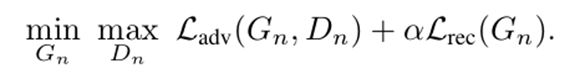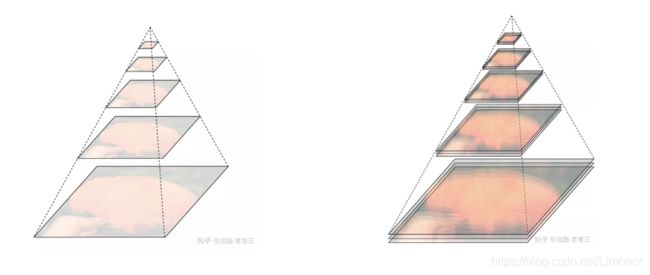CV笔记02：单图训练的SinGAN

SinGAN

从单个训练图像中学到的图像生成。 我们提出SinGAN ,一种在单个自然图像上训练的新的无条件生成模型。 我们的模型使用专用的多尺度对抗训练方案来跨多个尺度学习图像的补丁统计信息； 然后可以将其用于生成新的逼真的图像样本，该样本在创建新的对象配置和结构的同时保留原始补丁分布。

一、SinGAN是什么？

• SinGAN，这是一个可以从单张自然图像学习的非条件性生成式模型。
• 这个模型可以捕捉给定图像中各个小块内的内在分布，然后利用学到的信息，生成高质量、更多样性的样例，这些样例有着与原图相似的图像内容。
• SinGAN的结构是多个全卷积GANs组成的金字塔，这些全卷积GANs都负责学习图像中的某个小块中的数据分布，不同的GANs学习的小块的大小不同。
• 这种设计可以让它生成具有任意大小和比例的新图像，这些新图像在具有给定的训练图像的全局结构和细节纹理的同时，还可以有很高的可变性。
• 与此前的从单张图像学习GAN的研究不同的是，该方法是一个非条件性模型（也就是说它是从噪声生成图像的）。

三个关键字：单个自然图像 、非条件生成模型 、 内部尺度分布

作用是：生成高质量图像（同时又可以保持训练图像的整体结构和精细的纹理特征）

举例：油画作品变化、图片编辑、图像物体融合、 超分辨率图像、动画生成

二、背景和相关工作

• 普通GAN的应用情况使用已经比较全面，但是对训练数据集有限制。
• 本文将GAN带入了一个新领域–从单幅自然图像中学习非条件生成模型。单幅自然图像通常具有足够的内部统计信息，可以使网络学习到一个强大的生成模型。
• 作者提出了一种具有简单统一架构的模型SinGAN，能够处理包含复杂结构和纹理的普通自然图像，而不必依赖于具有同一类别图像的数据集。这是通过金字塔结构的全卷积GAN实现的，每个GAN负责捕捉不同尺度的图像分布。

文章中反复强调：

1. SinGAN：一种在单幅自然图像上训练的新型非条件生成模型
2. 训练数据源是来自单个图像
3. 一个统一的模型

作者提出sinGAN，打破了两个限制。SinGAN就在一张图像上训练，不在乎图像的类别，不管数据集都单类的人脸数据等，还是多类的分类数据等，都只在一张图像上训练，自然不在乎图像的类别的。采用Unconditional GAN能处理很多种任务同样是首创。

另一方面， 从新的角度上诠释了生成图像。以往的GAN，往往都在提供了某一类的众多的图像作为训练集，然后生成器学习到这些样本中的相同特征的分布。比如说人脸都有眼睛嘴巴等。那么我就用人脸举例子。然后测试的时候，输入噪声，网络就能输出带有人脸特征的人脸了。但SinGAN从新的角度，不去学习人脸类的共同特征，转而学习单一人脸图像的数据分布，这样网络可以生成这个人的脸，同时可能有不同视角下的这个人的脸。

三、模型

1. 文章的目的

我们的目标是学习一个无条件的生成模型，该模型捕获单个训练图像x的内部统计数据。

此任务在概念上与常规GAN设置相似，不同之处在于，此处训练样本是单幅图像不同尺度下的采样图像，而不是数据集中的整个图像样本。

模型选择处理更一般的自然图像，赋予模型生成纹理外的其他功能。为了捕捉图像中目标形状和排列位置这样的全局属性（如天空在顶部，地面在底部），以及精细的细节和纹理信息，SinGAN包含具有层级结构的patch-GANs（马尔可夫判别器），其中每个判别器负责捕捉x不同尺度的分布，如模型图所示。GAN的接收场较小，容量有限，因此无法记住单个图像。

虽然在GAN中已经探索使用了类似的多尺度结构，但本文还是第一个为从单幅图像进行内部学习而探索的网络结构。

2. 方法

SinGAN在仅仅一张图像上训练，这张图片既是训练样本也是测试样本。在这张图像上训练完了之后，同样在这样图片上测试。如果你想换一张图像测试，就必须先在那张图像上训练，这是有异于其他GAN的。

作者把原图按照一定的比例下采样，得到很多的下采样版本的图像，作者称这些样本为patch，用这些patches训练（patch的意思一般都是指从原图crop）

SinGAN采用无条件GAN方式设计，而且是级联式的Generator-Discriminator pair的形式。每一个G-D都负责一种尺度。作者发现，通过学习patch内部的数据分布，网络最终能在测试时输出保留原图中目标的结构以及形象，但是又不同于原图的真实图像。

3. 模型的结构

• 多尺度结构
• 单尺度模型
• 层级结构马尔科夫判别器

The generation of an image sample starts at the coarsest scale and sequentially passes through all generators up to the finest scale, with noise injected at every scale.

图像样本的生成从最粗的尺度开始，依次通过所有生成器，直到最细的尺度，在每个尺度注入噪声。

All the generators and discriminators have the same receptive field and thus capture structures of decreasing size as we go up the generation process.

所有的生成器和判别器都有相同的接收域，因此在生成过程中捕获的结构尺寸都在减小。

1) 生成器

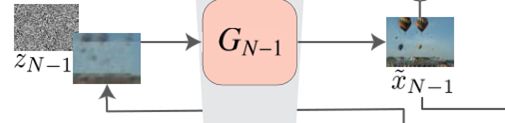
从最下面看开始看。先看G生成器这边，假设有N个尺度，最下面的第N个尺度是最粗糙的，最上面的尺度是最细的（finest）。

当处于最粗糙尺度时

$${\tilde{x}}_N=G_N(z_N)$$
在粗尺度上，这一代是纯生成，即 $Gn$ 映射空间高斯白噪声 $z_N$ 到图像样本 ${\tilde{x}}_N$。这一层的有效接受域通常为图像高度的一半，因此 $G_N$ 会生成图像和对象全局结构的总体布局。

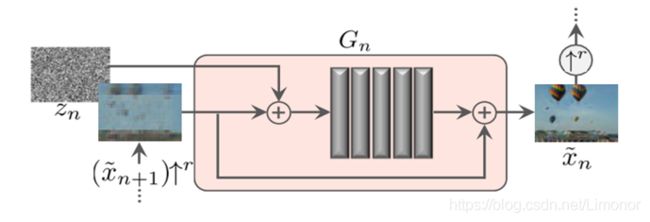
处于上面的N-1个更小尺度

$${\tilde{x}}_n=G_n(z_n,({\tilde{x}}_{n+1}){\uparrow }^r),n<N$$
添加了以前的尺度没有生成的细节。因此，除了空间噪声 $z_n$ 外，每个生成器 $G_n$ 还接受较粗尺度图像的上采样版本。即最下面的 $G$ 的输入是高斯噪声 $z_N$ ，输出 ${\tilde{x}}_N=G_N(z_N)$，然后 ${\tilde{x}}_N$ 上采样得到 ${\tilde{x}}_N{\uparrow }^r$ ，送到 $G_{N-1}$ 中，同时送进 $G_{N-1}$ 的还有$z_{N-1}$ ，以此类推。

图像样本的生成从最粗糙的级别开始，然后依次通过所有生成器，直到最精细的级别，并在每个级别注入噪声。所有的生成器和鉴别器都具有相同的接收域，因此在生成过程中捕获的结构尺寸都在减小。

2) 判别器

判别器 $D_{\tilde{x}}$ 和经过resize的patch x送到D中，和普通GAN的思路一样。论文采用的D是马尔科夫判别器，G和D的结构是相同的。（马尔科夫判别器在补充知识点有介绍）

3) 单尺度图像

其中ψn是一个有着5个Conv(3×3)-BatchNorm-LeakyReLU卷积块。我们在最粗糙的尺度上从每个块32个内核开始，然后每4个尺度增加2倍。因为生成器是全卷积的，所以我们可以在测试时生成任意大小和宽高比的图像(通过改变噪声图的尺寸)。

这张图具体来说，就是噪音 $z_n$ 是添加到图像$({\tilde{x}}_{n+1}){\uparrow }^r$ ，将噪声图和图像叠加后输入网络，送入一个卷积序列层，将网络输出与原图叠加后作为最终的输出。网络学习到的将是图像中缺失的细节信息（G输出的是后一个尺度所丢失的细节）。这确保了GAN不会忽略噪声。而卷积层的作用是生成的遗漏的细节 $({\tilde{x}}_{n+1}){\uparrow }^r$ （残差学习的思想）。输出的丢失细节加上上采样得到的更粗糙的图，就变成了更细化更具体的图。

4) 训练过程

从最大到最小尺度顺序地训练多尺度结构。一旦每个GAN被训练，它就会被固定下来。

我们可以先将图像缩小，再切出大图像块来训练。这样图像块分辨率低，容易训练，并且也保留了图像的整体信息。举个例子，对于原先200x200分辨率的图像，我们先降采样到40x40，再切成若干个11x11的块，能切出约800个，再用这800多个图像块训练GAN，生成的图像块应当保留了图像整体的布局信息。

虽然这样生成的图像很模糊，但我们已经有了一个整体的大致结构，只需要给图像上加上细节就可以了。不难想到，我们之前在原始图像上切出的11x11小图像块训练的GAN模型就有了意义，里面包含了我们目前所需要的细节信息。

再多加几个尺度进来，从最模糊的图像逐步加入细节。
SinGAN使用多个GAN结构分别学习了不同尺度下分辨率11x11的图像块的分布，并从粗糙到细致、从低分辨率到高分辨率逐步生成真实图像。

4. 关于感受野

这里有5个3x3的卷积层构成，感受野是11x11。

而最粗的那一个尺度上，输入的是原图经过下采样最小的patch，经过固定的11×11的感受野，因为输入的图像是原图缩小到很小的patch，即便是网络仅有很小的感受野，也能覆盖掉输入图像很大的区域，对应回原图，就是很大的区域。而越往细的尺度上，由于输入图像越来越大，感受野不变，能覆盖的尺度会越来越小。所以effective patch size越来越小，但也越关注细节，所以输出图像的细节更加丰富，逼真。

论文中也说明了小感受野的好处

5. 两种损失

• 对抗损失
• 重建损失

Adversarial loss

WGAN-GP:针对WGAN的问题的一种改进

Reconstruction loss

损失函数由adversarial loss和reconstruction loss两部分组成。其中adversarial loss使用了WGAN-GP loss，可以认为是文初提到的GAN loss的升级版，可以提升训练稳定性。reconstruction loss的目的是希望存在一组随机噪声输入，最终输出的图像就是原图。

四、实验应用

我们将探讨SinGAN在许多图像处理任务中的应用。为此，我们在训练后使用我们的模型，不进行架构更改或进一步调优，并对所有应用采用相同的方法。该思想是利用这样一个事实，即在推理时，SinGAN只能生成与训练图像具有相同patch分布的图像。因此，可以通过在n < N的某个尺度将图像(可能是向下采样的版本)注入到生成金字塔中，并通过生成器将其前馈传输，从而使其patch分布与训练图像的patch分布匹配，从而进行操作。不同的注入规模导致不同的效果。我们考虑以下应用。

1、paint-to-image（绘画到图像）：

在目标图像上训练SinGAN，在测试时将剪切画进行下采样将其输入到一个粗尺度中（n-1或n-2），

保留了画面的整体结构，真实地生成了与原图匹配的纹理和高频信息。

2、Harmonization（协调性）：

把粘贴的对象与背景图像融为一体，在原始图片（背景图）上进行SinGAN训练，在测试时将要粘贴的部分进行下采样，最后根据背景图像调整其外观和纹理（取得相对的平衡）。

3、Editing（编辑）：

在原始图像上找到要编辑的对象（建筑物），将它们组合到一起给SinGAN来训练，训练输出的结果与原始图像结合，重新生成一个图像。

4、Animation（图像到动画）：

从单个图像上来合成动图

如：一群鸟的图像中，模型可以获取鸟的所有羽翼的姿势（闪电也如此）

5、Super-resulation（超分辨率）：

通过因子s为输入的图像增加分辨率。先训练低分辨率图像，其中加入了一个重构损失，给了一个=的权重，并且加入了金字塔尺度因子 $r=\sqrt[k]{s}$ 。因为一些小结构倾向于在整个图的多个尺度反复出现，所以在测试时，作者通过因子r 为低分辨率上采样，然后和噪声一起作为输入送到最后一个生成器 $G_0$ 中。之后反复重复上述步骤 $k$ 次，最终得到高分辨率的图像。

尺度影响

在测试中的尺度影响

因为网络是多级的，在训练中有N个尺度，但是在测试中，可以使用更少的尺度，或者改变所使用的的尺度，来控制生成图像的变化。比如从第N-2个尺度开始，就会生成一些更真实的样本。下图的对比中，可以发现，从第N个尺度生成的斑马，有很多条腿。但是从第N-1个尺度开始，生成的样本就很真实了。而且对于细节保留的更多。

在训练中尺度的影响

选择更丰富的尺度，能捕获全局的结构，也是因为感受野大了。
尺度数目越小（意味着本身就从一个很细化的patch开始训练），仅仅能捕获到局部的纹理细节。丢失了全局的结构内容。

如何评价GAN网络的好坏？

在对抗生成网络中，生成器能骗过判别器 —> 出色；判别器能查出生成器 —> 出色。

但是判别器不能很好的衡量生成图片的质量和多样性。

通常，我们使用IS（inception score）和FID（Fréchet Inception Distance）这两个指标来评价不同的GAN模型。

相较于IS来说，FID会对模型坍塌这种问题更加敏感，所以更加适合GAN的学习。

共同的缺点：不适合描述模型的空间关系

文章采用了AMT和FID两种度量标准

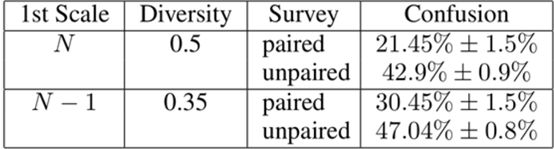
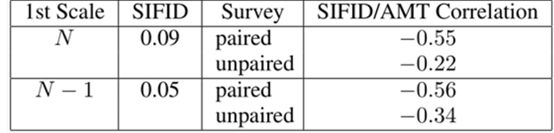
AMT：衡量生成图片的质量和多样性

解释：

（1）在非配对的情况下，混淆度更大；

（2）随着图片多样性的增多，混淆度会减小

FID（Fréchet Inception Distance ）

本文用到的真实图像和生成图像的深度特征的偏差
$$FID(x,g)=||{\mu }_x-{\mu }_g|{|}_2^2+Tr(\sum _x+\sum _g-2(\sum _x\sum _g{)}^{\frac{1}{2}})$$
较低的FID表示图片具有较高的质量和多样性。

解释：N-1生成的SIFID值低于N生成的，说明N-1级的图片具有较高质量和多样性

五、创新点

• 训练样本是单个图像，不是数据库中的样本集。
• SinGAN改善了上述不足，生成器Gn和判别器Dn使用同一个感受野，是第一个从单个图像进行内部学习的探索者；
• 与之前所有GAN相比，SinGAN定义的损失是针对所有图像的（并不是对于随机样本的损失）— 这允许网络可以学习边界条件。

六、结论

该论文介绍了一种可以从单幅自然图像中学习的新型非条件生成框架–SinGAN。证明了其不仅可以生成纹理，还具有为复杂自然图像生成各种逼真样本的能力。作者通过实验证明，SinGAN可以为多种图像处理任务提供非常强大的工具。

存在问题：

例如，如果训练图像只包含一条狗，SinGAN不会生成不同犬种的样本。

补充知识点

1. 图像金字塔

一组不同分辨率的图像。将不同scale 的图像送入网络提取出不同scale 的特征做融合，对于整个网络性能的提升很大。

采样方法：重叠和不重叠采样，如果是不重叠的，采样尺度因子为2，那就是每增加一层，行列分辨率为原来的1/2。如果是重叠的，采样尺度因子 r > 1时，分辨率的放大倍数将为γ^n 。

2. 多尺度学习

多尺度：对信号的不同粒度的采样

粒度越大（稀疏的采样）可以看到整体趋势（左图），但粒度越小（更密集的采样）可以看到更多的细节（右图）。

如果你的任务是判断图片中是否有前景（12*8）

如果你的任务是识别图片中的水果（64*48）

如果你的任务是后期合成该图片的景深（640*480）

3. patch-GANs（马尔可夫判别器）

它完全由卷积层构成，最后输出的是一个n$\times$n的矩阵，最后取输出矩阵的均值作为True/False的输出。

输出矩阵中的每一个输出，代表着原图中一个感受野，对应了原图的一片（patch），而具有这样结构的GAN被称为PatchGAN。（黄色部分**–patch**大小就是跟感受野有关）

每一层感受域的计算公式为：

图像中感受野：

结论：

Scale越大时 $\to$ fake和real在大致区域上会比较像

Scale较为精细时 $\to$ 两者在细节上已经比较像了。

4. 梯度消失，梯度爆炸

以前馈神经网络为例，假设存在一个网络结构如图：

其表达式为：$f(w_1)=f_3(w_3{f}_2(w_2{f}_1(w_1)))$

对表达式进行链式求导后：$\frac{\partial f}{\partial w_1}=\frac{\partial f_3}{\partial f_2}{w}_3\times \frac{\partial f_2}{\partial f_1}{w}_2\times \frac{\partial f_1}{w_1}$

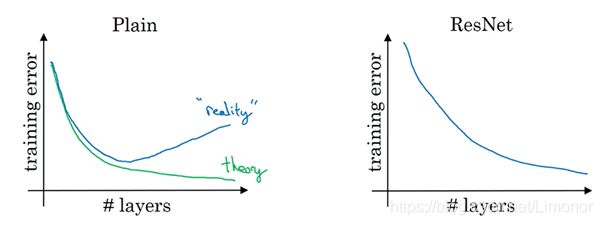
5. 残差网络resnet

解决梯度消失或梯度爆炸，让网络达到更深。由多个残差块构成。

残差块（Residual block）：远跳连接，可以训练更深的网络，也不会使得训练到越深损失不可控的问题。它可以根据残差块的不同使得网络变得简单。

使用残差网络“解决”梯度消失

论文参考：Deep Residual Learning for Image Recognition

或者参考我的上一篇残差网络的笔记 CV笔记01：残差网络学习

6. 采样

上采样（upsampling）：

保证分辨率的前提下来放大图像，使得放大后的图像能够在更高的分辨率的屏幕上显示。

三种方式：插值法 (Interpolation) 、反卷积 (Deconvolution) 和 反池化 (unPooling)

要将图像分辨率提升s倍，上采样因子，$r=\sqrt[k]{s}k\in N$

下采样（downsampling）：

生成图像的缩略图

原理：对一个M$\times$N的图像，进行s倍的下采样（s是m，n的公约数），用一个s$\times$s的窗口来取m$\times$n的图像的一个像素。最后的得到的这个像素点的值（pk）是s$\times$s窗口内所有像素点（Ii）的均值：
$$p_k=\sum _{i\in win(k)}\frac{I_i}{s^2}$$