XGBoost和Boosted Trees
树模型简介
树模型是工业界用得非常多的一个模型,它的representation类似于下图。其实基于树的模型都是通过一个个平行于坐标轴的平面去拟合训练集的实际分界面,理论上足够多的平行于坐标轴的平面能够拟合任意分界面。
![]()
Boosted Trees
XGBoost是“Extreme Gradient Boosting”的缩写,其中“Gradient Boosting”一词由Friedman在论文《Greedy Function Approximation: A Gradient Boosting Machine》中提出。XGBoost基于这个原始模型。本文是一个gradient boosted trees(梯度提升树)的教程,大部分内容是基于xgboost的作者的slides。
监督学习的要素
模型和参数
监督学习中的model通常是指给定输入 x i x_i xi如何去预测输出 y i y_i yi的数学结构。例如,一个常见的模型是 linear model,其预测是由 y ^ i = ∑ j θ j x i j \hat{y}_i = \sum_j \theta_j x_{ij} y^i=∑jθjxij给出的,这是输入特征的线性加权组合。 其实这里的预测 y y y可以有不同的解释,取决于做的任务,如回归或分类。 例如,可以通过 logistic 转换得到 logistic regression 中正类别的概率,当我们想要对输出结果排序的时候,也可以被用作排序得分。
parameters 是我们需要从数据中学习的未确定部分。在线性回归问题中,参数是系数 w w w。 通常我们使用 Θ \Theta Θ来表示参数。
目标函数:训练损失 + 正则
基于对 y i y_i yi的不同理解,我们可以得到不同的问题,比如回归,分类,排序等。我们需要找到一种方法来找到训练数据的最佳参数。为了做到这一点,我们需要定义一个所谓的 objective function 来衡量给定一组参数的模型的性能。
关于目标函数的一个非常重要的事实是,它们 must always 包含两个部分:training loss 和 regularization。
O b j ( Θ ) = L ( Θ ) + Ω ( Θ ) Obj(\Theta) = L(\Theta) + \Omega(\Theta) Obj(Θ)=L(Θ)+Ω(Θ)
其中 L L L是训练损失函数, Ω \Omega Ω是正则化项。 training loss 衡量我们的模型在训练数据上的预测性。 例如,常用的训练损失是 mean squared error(均方误差,MSE)。
L ( θ ) = ∑ i ( y i − y ^ i ) 2 L(\theta) = \sum_i (y_i-\hat{y}_i)^2 L(θ)=i∑(yi−y^i)2
另一个常用的损失函数是 logistic 回归的 logistic 损失。
L ( θ ) = ∑ i [ y i ln ( 1 + e − y ^ i ) + ( 1 − y i ) ln ( 1 + e y ^ i ) ] L(\theta) = \sum_i[ y_i\ln (1+e^{-\hat{y}_i}) + (1-y_i)\ln (1+e^{\hat{y}_i})] L(θ)=i∑[yiln(1+e−y^i)+(1−yi)ln(1+ey^i)]
regularization term(正则化项) 是人们通常忘记添加的内容。正则化项控制模型的复杂度,有助于避免过拟合。 这听起来有些抽象,那么我们在下面的图片中考虑下面的问题。在图像左上角给出输入数据点的情况下,要求您在视觉上拟合一个 step function(阶梯函数)。 您认为三种中的哪一种解决方案是最拟合效果最好的?
为什么要介绍一般原则
上面介绍的要素构成了监督学习的基本要素,它们是机器学习工具包的基石。例如,你应该能够描述boosted trees和random forests之间的差异和共同点。以正式的方式理解这个过程也有助于我们理解我们正在学习的目标以及启发式算法背后的原因,例如pruning和smoothing。
Tree ensembles
我们已经介绍了监督学习的要素,接下来开始真正的trees吧。首先,让我们先来了解一下 xgboost 的模型 : 集成树。 集成树模型是一组分类和回归树(CART)。 这里有一个 CART 的简单的示例,它可以分类某人是否会喜欢电脑游戏。
我们把一个家庭的成员分类到不同的叶子,并在相应的叶子节点上给他们分配分数。 CART与 decision trees有一些不同,decision trees叶子只包含决策值。在 CART 中,每个叶子都有一个真实的分数,这给了我们除了分类外更丰富的解释。 这也使统一的优化步骤更加容易,我们将在本教程的后面部分看到。
通常情况下,单棵树由于过于简单而不够强大到可以在实践中使用。实际中使用的是集成树模型,它将多棵树的预测加到一起。
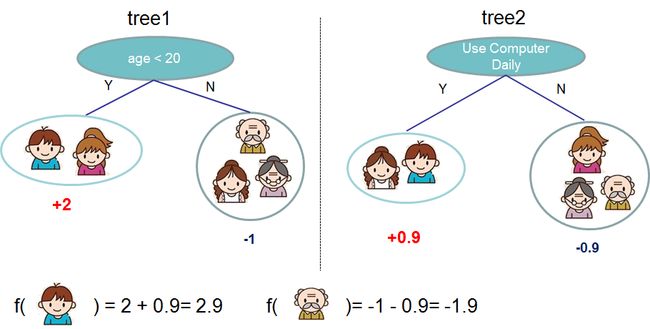
上图是两棵树的树集成的例子。将每棵树的预测分数加起来得到最终分数。如果你看一下这个例子,一个重要的事实就是两棵树试图相互补充。数学上,我们可以把模型写成
y ^ i = ∑ k = 1 K f k ( x i ) , f k ∈ F \hat{y}_i = \sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F} y^i=k=1∑Kfk(xi),fk∈F
其中 K K K是树的数量, f f f是函数空间 F \mathcal{F} F中的一个函数, F \mathcal{F} F是所有可能的CARTs的集合。因此我们优化的目标可以写成
obj ( θ ) = ∑ i n l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) \text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k) obj(θ)=i∑nl(yi,y^i)+k=1∑KΩ(fk)
那么问题来了,随机森林的模型是什么?就是树集成!所以 random forests 和 boosted trees 在模型上并没有什么不同,不同之处在于我们如何训练它们。这意味着如果你写一个 tree ensembles 的预测服务,你只需要编写它们中的一个,它们应该对random forests和 boosted trees都支持。这也是监督学习基石元素的一个例子。
Tree Boosting
在介绍完模型之后,我们从真正的训练部分开始。我们应该怎么学习trees呢? 答案是,像所有的监督学习模型一样:定义一个目标函数,然后优化它!
假设我们有以下目标函数(记住它总是需要包含训练损失和正则化)
obj = ∑ i = 1 n l ( y i , y ^ i ( t ) ) + ∑ i = 1 t Ω ( f i ) \text{obj} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) obj=i=1∑nl(yi,y^i(t))+i=1∑tΩ(fi)
Boosting的思想可以看成一种参数更新的思路,只不过这个参数是一个子树。通过生成一颗子树叠加到之前的子树上来减小损失函数。
Additive Training
我们要学习的是 f i f_i fi函数,每个函数都包含树的结构和叶子分数。这比传统的最优化问题要难得多。一次性训练所有的树并不容易,我们使用加法训练:固定好已经训练完的树,然后一次添加一棵新的树。运用加法训练,目标不再是直接优化整个目标函数,这已经被我们证明是行不通的。而是分步骤优化目标函数,首先优化第一棵树,完了之后再优化第二棵树,直至优化完K棵树。 我们把在 t t t步的预测值写做 y ^ i ( t ) \hat y_i^{(t)} y^i(t),所以有
y ^ i ( 0 ) = 0 y ^ i ( 1 ) = f 1 ( x i ) = y ^ i ( 0 ) + f 1 ( x i ) y ^ i ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y ^ i ( 1 ) + f 2 ( x i ) … y ^ i ( t ) = ∑ k = 1 t f k ( x i ) = y ^ i ( t − 1 ) + f t ( x i ) \begin{aligned}\hat{y}_i^{(0)} &= 0\\ \hat{y}_i^{(1)} &= f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ &\dots\\ \hat{y}_i^{(t)} &= \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)\end{aligned} y^i(0)y^i(1)y^i(2)y^i(t)=0=f1(xi)=y^i(0)+f1(xi)=f1(xi)+f2(xi)=y^i(1)+f2(xi)…=k=1∑tfk(xi)=y^i(t−1)+ft(xi)
另外还有一个问题,每一步我们想要哪棵tree呢?一个自然而然的事情就是添加一个优化我们目标的方法。
obj ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t ) ) + ∑ i = 1 t Ω ( f i ) = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t \begin{aligned}\text{obj}^{(t)} & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) \\ & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + constant \end{aligned} obj(t)=i=1∑nl(yi,y^i(t))+i=1∑tΩ(fi)=i=1∑nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+constant
如果我们考虑使用 MSE 作为损失函数,它将是下面的形式。
obj ( t ) = ∑ i = 1 n ( y i − ( y ^ i ( t − 1 ) + f t ( x i ) ) ) 2 + ∑ i = 1 t Ω ( f i ) = ∑ i = 1 n [ 2 ( y ^ i ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 ] + Ω ( f t ) + c o n s t a n t \begin{aligned}\text{obj}^{(t)} & = \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) \\ & = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + constant \end{aligned} obj(t)=i=1∑n(yi−(y^i(t−1)+ft(xi)))2+i=1∑tΩ(fi)=i=1∑n[2(y^i(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)+constant
MSE 的形式比较友好,具有一阶项(通常被称为残差)和二次项。 对于其他形式的损失(例如,logistic loss),获得这么好的形式并不是那么容易。 所以在一般情况下,我们把损失函数泰勒展开到二阶
O b j ( t ) = ∑ i = 1 n [ l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) + c o n s t a n t Obj^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + constant Obj(t)=i=1∑n[l(yi,y^i(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)+constant
其中 g i g_i gi和 h i h_i hi被定义为
g i = ∂ y ^ i ( t − 1 ) l ( y i , y ^ i ( t − 1 ) ) h i = ∂ y ^ i ( t − 1 ) 2 l ( y i , y ^ i ( t − 1 ) ) \begin{aligned}g_i &= \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)})\\ h_i &= \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)}) \end{aligned} gihi=∂y^i(t−1)l(yi,y^i(t−1))=∂y^i(t−1)2l(yi,y^i(t−1))
我们删除了所有的常量之后,t步中的具体目标就变成了
∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)
这成为了这棵新树的优化目标。这个定义的一个重要优点是它只依赖于 g i g_i gi和 h i h_i hi。这就是 xgboost 如何支持自定义损失函数。 我们可以使用完全相同的使用 g i g_i gi和 h i h_i hi作为输入的 solver(求解器)来优化每个损失函数进,包括 logistic regression 和 weighted logistic regression。
模型复杂度
我们已经介绍了训练步骤,但是等等,还有一个重要的事情,regularization(正则化)! 我们需要定义树的复杂度 Ω ( f ) \Omega(f) Ω(f) 。为了做到这一点,让我们首先改进一棵树的定义 f ( x ) f(x) f(x)如下
f t ( x ) = w q ( x ) , w ∈ R T , q : R d → { 1 , 2 , ⋯ , T } . f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} . ft(x)=wq(x),w∈RT,q:Rd→{1,2,⋯,T}.
这里 w w w是叶子上的分数向量, q q q是将每个数据点分配给对应叶子的函数, T T T是叶子的数量。 在 XGBoost 中,我们将复杂度定义为
Ω ( f ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2 Ω(f)=γT+21λj=1∑Twj2
当然有不止一种方法来定义复杂度,但是这个具体的方法在实践中运行良好。正则化是大多数树的包不那么谨慎或简单忽略的一部分。这是因为对传统的树学习算法的对待只强调提高 impurity(不纯性),而复杂度控制则是启发式的。 通过正式定义,我们可以更好地了解我们正在学习什么,它在实践中也运行良好。
结构分数
这是 derivation(派生)的神奇部分。在对树模型进行重新格式化之后,我们可以用第 t t t棵树来编写目标值:
O b j ( t ) ≈ ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \begin{aligned}Obj^{(t)} &\approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\\ &= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T \end{aligned} Obj(t)≈i=1∑n[giwq(xi)+21hiwq(xi)2]+γT+21λj=1∑Twj2=j=1∑T[(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2]+γT
………………
obj ( t ) = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T obj(t)=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT
w j ∗ = − G j H j + λ obj ∗ = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T \begin{aligned}w_j^\ast &= -\frac{G_j}{H_j+\lambda}\\ \text{obj}^\ast &= -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T\end{aligned} wj∗obj∗=−Hj+λGj=−21j=1∑THj+λGj2+γT

如果所有这些听起来有点复杂,让我们看看图片,看看如何计算得分。简单的说,对于给定的树结构,我们将统计信息 g i g_i gi和 h i h_i hi推送到它们所属的叶子,将统计数据加在一起,并使用公式计算树的好坏。 这个分数就像决策树中的不纯度,不过它还考虑了模型的复杂度。
学习树结构
既然我们有了一个方法来衡量一棵树有多好,理想情况下我们会列举所有可能的树并挑选出最好的树。 在实践中,这种方法是比较棘手的,所以我们会尽量一次优化树的一层。 具体来说,我们试图将一片叶子分成两片,得到增加的分数
G a i n = 1 2 [ G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ ] − γ Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma Gain=21[HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2]−γ
这个公式可以分解为 1) 新左叶上的得分 2) 新右叶上的得分 3) 原始叶子上的得分 4) 附加叶子上的正则化。 我们可以在这里看到一个重要的事实:如果增益小于 λ \lambda λ,我们最好不要添加那个分支。这正是基于树模型的 pruning(剪枝)技术!通过使用监督学习的原则,我们自然会想到这些技术有效的原因 ?
对于真正有价值的数据,我们通常要寻找一个最佳的分割。为了有效地做到这一点,我们把所有的实例按照排序顺序排列,如下图所示。
然后从左到右的扫描就足以计算所有可能的拆分解决方案的结构得分,我们可以有效地找到最佳的拆分。
XGBoost 最后的话
既然你明白了什么是 boosted trees 了,你可能会问这在 XGBoost 中的介绍在哪里? XGBoost 恰好是本教程中引入的正式原则驱动的工具! 更重要的是,它在 systems optimization(系统优化) 和 principles in machine learning(机器学习原理) 方面都有深入的研究。 这个库的目标是推动机器计算限制的极限,以提供一个 scalable(可扩展), portable(可移植) 和 accurate(精确的) 库。 确保你尝试了它,最重要的是,向社区贡献你的智慧(代码,例子,教程)!
##参考:
Introduction to Boosted Trees
https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf