元启发式 启发式_启发式出现的思维弯曲世界可能意味着我们是人造的
元启发式 启发式
想象一下中奖!
我知道。 有什么机会吧?
一秒钟,逗我一下。
假装我们正在玩赢强力球大奖。 在您的脑海中,选择5个正确的数字以及正确的强力球。 只要您有计算器,就可以很容易地计算出赔率:
5/69 x 4/68 x 3/67 x 2/66 x 1/65 x 1/26 = 120/35 064160560 = 1/292 201338
为了论证,我们说这是两亿九千万。 可以使用科学符号以更简洁的方式编写两亿九千万:
2.9 x10⁸
2.9乘以10连续八次。
这是一个很大的数字。 如此之大,以至于在不真正意识到它有多大的情况下,就可以简单地将其作为“ 大数字 ”丢弃。
为了获得一些观点,我们可以将其与闪电袭击的可能性进行比较。 我们大多数人并不特别担心被雷击,因为机会太少了。
根据《 国家地理》杂志的数据 ,在美国一年内被雷击的几率是70万比1或7 x10⁵。
那么赔率如何增加呢?
在被雷击的几率与赢得彩票的几率相匹配之前,您必须生存417年以上。
到目前为止和我在一起?
太好了,这就是我们的热身工作。 让我们开始看一些实数。
头顶上,您能想到的最小的东西是什么?
是否想到了氢原子 ?
好吧,可以肯定的是,有很多东西比氢原子还小-电子,夸克,许多亚原子粒子, 普朗克长度等等。
就我们的目的而言,一个氢原子就足够了。 主要是因为它是我们宇宙中最丰富的元素( 假设没有暗氢 ),因此它为大量类比提供了一个很好的基础。
为了了解氢气的数量,我们可以考虑一下一个250ml杯子中有多少水H2O分子。 使用称为水的摩尔质量的某种物质 ,我们知道18克水大约包含:
6.022 x10²³
水分子。 假设我们有一个250毫升的杯子。 我们知道分子总数将是:
250/18 x 6.022 x10²³= 8.36 x10²⁴
当然,一个水分子有两个氢原子,因此我们的氢原子总数为:
1.67 x10²⁵
现在是一个实数。
根据地球上所有海洋中所有水量的估计,海洋中250ml杯水的数量为:
5 x10²¹
这产生了相当惊人的结果。
一杯水中的分子比所有水中的杯子都要多。
我们可以通过简单的乘法来计算地球上所有水中所有氢原子的总数:
1.67 x10²⁵x 5 x10²¹= 8.35 x10⁴⁶
那已经过去了,但我们仍然可以考虑更大。
太阳。
太阳系统中约有99.8%的质量保持在太阳中 。 很大
它也主要是氢气( 尽管已将其融合到氦气和其他重元素中 ),这使其非常适合我们的用途。 对太阳中氢原子数的估计略高于:
10⁵⁷
您可能会以为地球上所有水中的氢原子数目都非常接近这个数目。 毕竟只少了10⁰。 实际上,这种差异仍然是中奖几率的34倍左右,因此它比看起来更大。
不过,太阳只是一个相当大的星系中的一颗恒星。
我们的银河系是一个大约十万光年的禁止旋转的星系,包含约1000亿太阳质量 。 估算整个银河中的氢原子数很简单:
10⁵⁷x10¹¹=10⁶⁸
整个宇宙中的恒星总数估计为10²³。 将存在的所有恒星中的氢原子总数:
10⁵⁷x10²³=10⁸⁰
现在,这是一个粗略的估计,但它也是一个很大的数字。
除了不是。
这是一个很小的数字。 微不足道。 微小的。
与NP-Hard ( 非确定性多项式Hard )问题的复杂性相比,没什么。
10英镑必须去幼儿园,学校,大学并获得十年的工作经验,才能与最温和的NP-Hard问题相提并论。
NP-硬问题的一种著名类型是旅行商问题 ( TSP )。 本质上,目标是找出最有效的方式来访问多个地点。 出于现实目的,我们通常希望考虑一个轻微的变化,称为多重旅行销售问题 ( mTSP) 。
mTSP有很多实际应用,尤其是在路由优化领域。 送货公司希望确保其车队尽可能高效地运行,以节省燃油,人工,磨损等方面的时间和金钱。
考虑一家小型运输公司,该公司有5辆车的车队和100辆车要完成。 绝不是不合理的现实情况。
对于此类问题,如果不检查每种可能性,就无法知道给定的解决方案是否是最佳解决方案。
从表面上看,这似乎并不难。 我们要做的就是找出各种可能性,尝试每种可能性,然后选择最好的可能性。
要确定有多少潜在的解决方案,我们可以重复以下过程,直到访问完所有位置为止:
1.从5辆车中选择1辆移至100个地点中的1个。
2.从5辆车中选择1辆,移至其余99个位置中的1个。
3.从5辆车中选择1辆,移至其余98个位置中的1个。
4.…
100.从5辆车中选择1辆到最后的剩余位置
要计算这将是一个很长的公式:
(1/5 x 1/100)x(1/5 x 1/99)x(1/5 x 1/98)x(1/5 x 1/97)x…x(1/5 x 1/1 )
为了获得排列的总数,我们可以更简洁地编写以下内容:
Vᴸx L!
其中V是车辆数,L是位置数。 感叹号是写出乘法序列的简写形式( 在我们的例子中是从100开始 ):
100 x 99 x 98 x 97 x…x 1
插入车辆数量为5,位置数量为100,我们得到以下数量:
7.88 x10⁶⁹x 9.33 x10¹⁵⁷= 7.36 x10²²⁷
请记住,整个已知宇宙中所有星系中所有恒星中的氢原子总数仅为10。 即使我们将宇宙的大小低估了100万倍,这个数字也只有10⁸⁶。
我们真的没有一种语言来描述这个数字比运行中的mTSP的复杂度小多少。
要检查这么多排列,我们将需要开始考虑可能需要花费多长时间。
由IBM为Oak Ridge国家实验室制造的SUMMIT超级计算机具有历史上( 迄今为止 )最快的处理能力。 这用称为FLOPS的东西来衡量, FLOPS代表每秒的浮点操作数 。
SUMMIT管理着可观的200 petaflops。 Peta表示10⁵,因此我们可以将SUMMIT中的petaflop数写为2 x 10⁷。 令人印象深刻的快速。
让我们非常慷慨,并假设一次翻牌等同于对我们问题中一种可能性的完整检查。 从本质上讲,这意味着我们每秒钟可以测试2 x 10 15个可能性。
在寻求帮助后,我们可以节省一些处理时间,解决问题,并在我们等待时去喝杯咖啡。 等一下 等一下 还有...
就是这个 以每秒2 x10¹⁷的速度进行检查:
7.36 x10²²⁷/ 2 x10¹⁷= 3.68 x10²²⁰秒
除以一分钟的分钟数,一小时的分钟数,一天的小时数,一年的天数,我们得到:
1.16 x10²⁰³年
这将使我们在其他等待轮到他们的科学家中不受欢迎。
我们的最佳估计告诉我们, 宇宙目前已有138亿年的历史,并且可能还会持续50亿年 -不管它是热死,紧缩还是大泪。
我们拥有50亿年,即5 x 10 x。 我们需要完成1.16 x10²⁰³的计算。 这有点令人沮丧。
数以百万计的SUMMIT超级计算机比宇宙的寿命长几万亿年,将无法检查我们规模适中的NP-Hard问题中的每个排列。
我们将需要找到解决该问题的另一种方法,以帮助送货公司降低成本。
一种可能性是使用量子计算,因为这将使我们能够同时( 理论上 )检验无限可能性。 不幸的是,我们还没有准备好量产,所以可能还需要几年的时间。
目前,我们仍停留在传统计算上。
如果硬件不能更改,则必须使用我们的方法。
可以不用反复使用蛮力来检查所有可能性,而可以尝试反复比较猜测的解( 近似值 )。 如果我们对如何产生这些猜测很明智,并且对从比较中得出的教训很聪明,那么就有可能产生非常好的结果( 即使我们永远无法证明这是最好的结果 )。
比较备选方案的算法( 与传统的过程算法相反,即采用预定义的一组步骤来得出结果 )被称为启发式算法 。 随着时间的推移,这些新兴的解决方案常常会从自然界中汲取灵感。
这里出现的单词很关键。
当系统显示出在其任何组成部分中均未观察到的特性时,就会发生出现。
我们的太阳系就是一个很好的例子。 通过重力作用下的气体和尘埃云,形成了一颗由行星和卫星以及生命本身组成的恒星,虽然最初并不存在,但随着时间的流逝而出现。
蚁群优化 ( ACO )模仿了蚂蚁在巢附近觅食的行为。 最初,蚂蚁向各个方向前进。 如果发现食物,它会回到巢中,留下一条微弱的信息素痕迹,可能会被连续的蚂蚁波捕获。
如果其他蚂蚁在同一个地方发现食物或资源,它们也会留下一连串的信息素,返回巢穴。 随着时间的流逝,这些信息素的踪迹逐渐积累,导致越来越多的蚂蚁直接跟随它们。 一段时间后,巢与周围资源之间便出现了非常直接和有效的运输路线。
这如何适用于mTSP?
一种方法是对解决方案进行10个( 或一百个或一千个 )随机猜测,并记录每个花费多少。 成本最低的猜测可能会使每个组成路线都标记有数字信息素。
一次又一次地重复此过程,以建立越来越强大的数字信息素轨迹,这些信息轨迹可能会开始如此轻微地影响连续猜测-偏向于降低成本( 因为我们只将信息素添加到每次迭代的最低成本结果中 )。
经过数以千计,数以千计或数万次的迭代后,相当强大的信息素踪迹累积了起来( 希望如此 )才是一种非常有效的解决方案。
ACO不是我们可以使用的唯一启发式算法。 模拟退火 ( 退火是在金属冷却时连续加热和加工金属的过程,以消除原子的晶体排列中的弱点 ), 遗传算法也增加了自己独特的启发式机会来产生更好的解决方案。
不同的启发式算法具有各自独特的优点和缺点,因此将它们组合在一起可以帮助更快地生成更好的解决方案。
能够描绘出现实世界中5辆车辆100个位置问题可能看起来像什么。
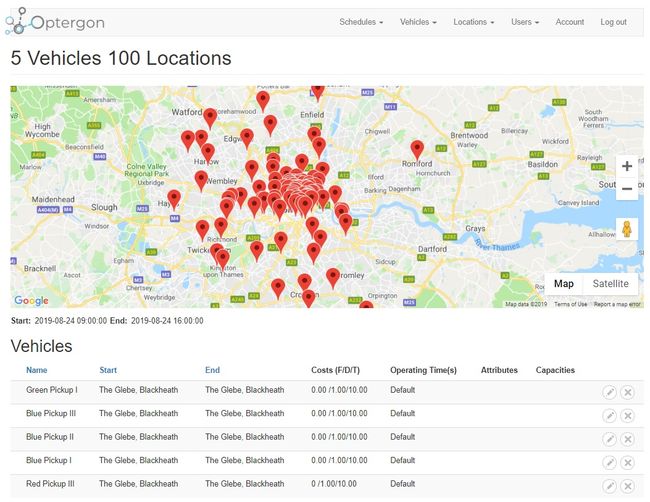
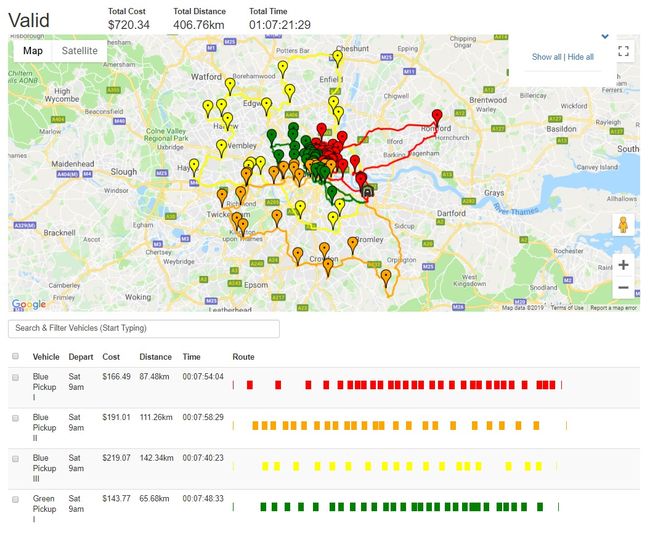
5辆汽车100个位置路线优化地图,由 Optergon提供
此屏幕快照显示了在伦敦周围散布的100个位置( 实际上,对于那些对旋风历史之旅感兴趣的人来说,这是一个很大的博物馆列表 )。
请注意,与现实世界一样,对问题本身的表述也有一些限制。
例如,车辆有营业时间。 在这种情况下,上午9点至下午4点之间。 它们具有与之相关的成本- 固定 , 距离和时间 。 在此示例中,距离成本( 包括燃料和磨损等 )设置为每公里1美元,时间成本( 例如驾驶员工资 )设置为每小时10美元。 这些费用将根据相关公司的特定运营成本进行更改( 例如,轻型皮卡车与大型卡车相比,基于距离的成本可能更低 )。
位置具有与之相关的时间。 重要的是要考虑到车辆为了完成其任务(即交付,提取或服务 )而需要停在某个位置的时间。
这是结果。
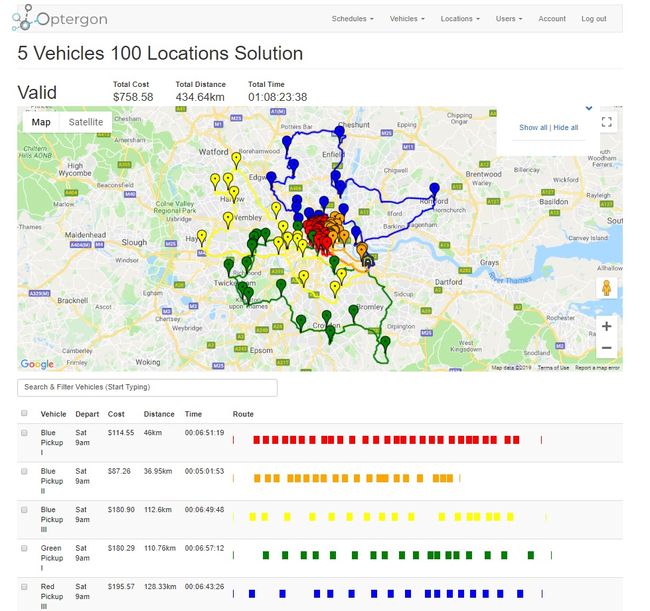
5车辆100位置路线优化解决方案,由 Optergon提供
此结果有一些有趣的特性,可能不会立即显现出来。
首先,它可以访问所有以按给定的时间框架提供的车辆的位置。 这个很重要。 无法很好地优化路线的公司需要扩展其机队,以便以显着更高的成本管理工作量。
其次,每辆车的路线有些重叠。 我们常常会直觉上期望每辆车都在其自己的地图小分区内工作。 实际上,这通常是优化算法内置的捷径的结果,这些捷径旨在降低问题的复杂性。
本质上,可以通过对地图进行划分并优化V个较小的问题( 其中V是车辆数 )来大大降低mTSP问题的复杂性。 为每辆车分配地图的分区以大致相等地划分位置,这会给我们带来以下复杂性( 仅大致来说,因为有许多方法可以划分表面 ):
(L / V)!ⱽ
插入5辆汽车和100个地点可得到:
(100/5)!⁵= 20!⁵= 8.5 x10⁹¹
问题的最初表述的复杂性可以忽略不计,仅为7.36 x10²²⁷。
这极大地减少了潜在解决方案空间的大小。 但是,它不是免费提供的。 总会有一个权衡。 由于极大地限制了可供探索的解决方案空间,因此降低复杂性所获得的结果可能会失去准确性。
在许多情况下,优化的路线将交叉和/或重叠。 尤其是在像伦敦这样的城市,那里有许多单向街道,动脉路线的移动速度明显快于较小,更直接的路线,时间,距离和车辆容量的限制等。
我们在这里使用的一个特殊问题是,城镇中心的位置密集且位置密集,周围的中心点周围有更远的外围点。 由于密集的中央集群中的位置比一辆车所能容纳的更多,因此有更多的人需要访问同一区域。
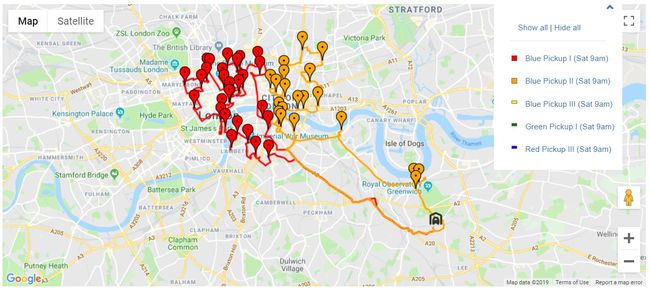
处理大量密集集群的两辆车需要先从车库沿着相同的高速公路行驶,然后再前往各自的位置。
部分差异化的路线由 Optergon提供
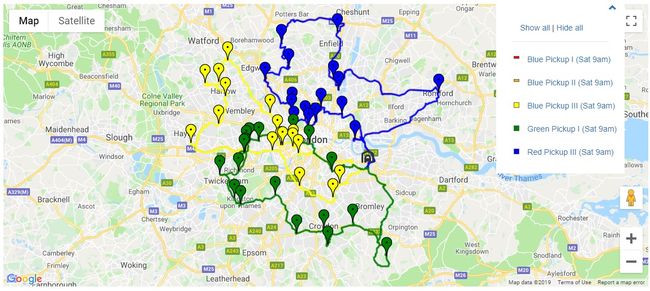
其他三辆车则处理了大部分偏远地区,同时拾取了一些集中地点作为其较长( 按距离 )路线的一部分。
Optergon 提供的部分重叠路线
如果允许车辆留出更多时间,您会期望什么? 他们可以从上午9点至下午5点工作,而不是从上午9点至下午4点工作。
这是结果。
降低成本和车辆路线由 Optergon提供
该解决方案便宜约5%。 满足所提出问题的需求所需的车辆更少。 至少,使用较少的车辆可以减少往返仓库的多余时间和距离。
同样,结果表明,即使有5辆车,该公司也有可能在特定时间范围内仅使用4辆车实现其目标。 另一个重要结果是,它显示了更小,更高效的机队如何潜在地降低成本。
到目前为止,使用的每辆车的成本都完全相同。 实际上,在不同类型的大型车队之间可能会有重大变化。 由于整个优化过程都是降低成本的一项工作,因此,重要的是要看到成本不均匀的影响。
假设一辆汽车比较旧,并且燃油消耗往往会更差。 每公里的路程成本上升至1.50美元。 另一辆车正由一位半小时的替换驾驶员驾驶,每小时15美元。
新的问题公式如下所示。
独特的时间和成本参数由 Optergon提供
现在,“绿色皮卡I” ( 清单顶部 )的距离成本为$ 1.50每公里。 Blue Pickup III ( 第二名 )现在的小时成本为15美元。 您期望结果有什么不同(如果有)?
这是新结果。
距离成本优化结果由 Optergon提供
结果稍贵。 可以预期,因为成本增加了。
使用了绿色皮卡I ( 距离费用增加了50% ),但总共行驶了49公里。 小于任何其他车辆距离的一半。
根本没有使用Blue Pickup III 。
回想一下,我们有五辆车可用,因此只有一辆昂贵的车才能成功实现所有目标。
您能猜测如果将时间范围缩短到上午9点至下午4点以强制使用所有五辆车会发生什么情况?
这是结果。
Optergon 提供的不对称距离和时间成本优化结果
显而易见 ,虽然必须使用Blue Pickup III ,但其操作时间却比其他任何车辆少30%。 在“ 绿色皮卡”行驶期间, 我的行驶距离远少于其他任何车辆,从而进一步降低了成本。
距离和时间成本之间的细微差别在塑造最佳结果中起着重要作用。 两者都很重要。 考虑两个成本参数会增加系统的复杂性,因为它现在必须平衡非对称成本条件。
从表面上看,这些结果似乎是令人满意的。 它们就是您所期望的,对吗? 常识。
想一想。
底层算法没有常识概念。 他们只操纵和比较备选方案。 但是,他们将以坚定不移的准确性取得我们所期望的结果-除非它们的表现超越我们( 最有可能是由于我们在问题开始时无法预见的情况 )。
同意启发式算法对我们的意义远大于对算法的意义。
人类不能希望执行优化这些类型问题所需的计算。 这不会阻止我们使用我们认为理所当然的各种抽象,技巧和思维飞跃来直观地知道预期的结果。
事实证明,我们是肉体上的试探者 。 我们的大脑实现它们,而我们的大脑和身体都通过它们进化。
像接球的日常任务是有技巧的,我们必须通过实践过来,以建立“替代品”,我们以预测的最大比较实时我们目前的情况的显著数量出现反复可能的结果( 并避免撞到鼻子 )。
启发式不仅被我们的思维所利用 ; 他们习惯于建立我们的思想。
DNA是数百万年遗传启发法的产物,这些遗传学法催生了新的适应能力强的个体,它们有可能生存和繁殖。
这里奇怪的是,一个自然的启发式过程( 即遗传进化 )出现了另一个有机的启发式过程( 常识,硬性地连接到我们的大脑中 )。
如果自然界一直在使用启发式方法和新兴方法通过重力和气体云产生智能生命,也许使用启发式方法解决NP-Hard问题是帮助我们产生远比mTSP解决方案意义深远的途径。
现在,启发式技术可以通过多种日常方式帮助您提高效率。 特别是在解决创造性问题时( 程序上不能强行解决 )。 SubMerge技术 ,在如何赚钱博客中的第12节中进行了说明。 是一个很好的例子,说明了如何将启发式方法应用于一系列日常创意问题,例如提出新的文章创意。
但是,归根结底,启发式方法可能是产生人工智能的一种好方法( 如果愿意,可以使用人工智能常识 )。
“选择性压力作用下的反复变化”是出现进化的确切场景。
仅根据非常简单的规则来控制哪些启发式程序是基于目的的适应性而 “ 生存 ”或“ 消亡 ”的,例如那些被编入康威《生活游戏》的规则 ,丰富而多样的,Swift发展的程序生态系统可能会确立自己的地位。
在这种情况下,适合用途的一个很好的例子可能是设计更好的芯片,更好的体系结构,创造力,更准确的天气模式预测,股市变化等。
各种竞争性计划对我们有价值的生态系统将为新兴的生态系统提供适合用途的一种潜在定义。 无法使用并失去处理资源。 使用并捕获其他资源。 在自然界中竞争(食物和资源,例如 饮用水,盐,住所等 )的类似物。
软件中的启发式出现将成为人工进化的驱动力,最终可能会导致自我意识的人工实体,就像物理启发式方法和出现会导致像我们一样的自我意识的自然生物一样。
唯一的区别是软件的发展将Swift发生。
非常快。
大自然花费了数百万年的时间,可能要花费数月,数周,然后数天的软件…
自我意识的软件是想探索我们的物理宇宙,还是建造冯·诺依曼机器来制造带FTL旅行的虫洞和/或船( 希望带我们同行 ),还是仅仅居住在自己的虚拟宇宙中,这是任何人的猜测。
除非它担心太阳系水平的灭绝事件,否则前一个选项对于软件来说似乎是不必要的过时,所以我赞成后者( 虚拟宇宙 )选项。
无论如何, 费米悖论暗示这是最可能的情况。
这导致一个极其令人不安的结论。
考虑以下原则:
已知大小的无序集合中的一个元素大于一个,则不应假定它是按集合唯一的。
完全公开:我提出了这一原则。 它很可能以一种形式或其他形式存在。
为了演示它的实际效果,请想象一大罐饼干。
您抓到的第一个饼干有巧克力片。
假设它是独特的,并且大罐子里没有其他饼干有巧克力片,这是否合理? 还是至少假设其他饼干中有巧克力片更合理?
我们可以对宇宙中的生活应用相同的论点。
考虑一个由大约10²的行星组成的宇宙。 观测到的第一个行星( 称为地球 )拥有丰富的生命。 您是否应该假设它是独特的,或者至少其他一些星球更有生命?
我们可以将此原理依次应用于宇宙。
考虑以下场景( 为论证起见,我们将其称为启发式智能Universe场景 ):
启发式智能出现在一个足以创建人造宇宙的宇宙中。 这意味着一组宇宙大于一个( 这在地球上没有必要发生,只是它可能在宇宙中的任何地方发生 )。
在一组已知的宇宙大于一个的情况下,我们不应该假设唯一性。
因此,我们的宇宙可能不是第一个( 因为这将使其在设定上具有唯一性 )。
这给我们留下了一个温和的结论,即我们可能存在于上述过程的某些迭代中,其中 人造宇宙是由出现从智能启发式方法应运而生 。
David为SME Pals(在线创业公司的博客)做出了贡献,并为包括Optergon在内的各种技术创业公司提供咨询。 他无法撼动我们在模拟中运行的感觉。
翻译自: https://hackernoon.com/how-the-mind-bending-world-of-heuristic-emergence-may-lead-to-artificial-universes-u79w32xu
元启发式 启发式