python数据分析实战：DCM模型设计及实现（以波音公司用户选择为例）

1.DCM介绍

离散选择模型DCM（Discrete Choice Model）是一类模型族，这个名字听起来有些陌生，但其包含的模型却是我们熟知的LR（Logistics Regression，逻辑回归模型），以及其变种MNL（MultiNomial Logit，多项Logit模型）和NL（Nested Logit，嵌套Logit模型）。
DCM可用于经济学中的选择问题，是分析“从有限互斥选项集中进行单项选择”的计量模型。主要包括五个部分：决策者（决策者属性）、备选项集合、备选项属性、决策准则和选择结果，数学表达式如下：
$$选择结果=F(决策者，备选项集合，备选项属性)$$
$F$是决策准则，即效用最大化准则。模型最终实现的功能是在给定决策者、备选项集合、备选项属性后，基于效用最大化准则，得到选择结果。

消费者内心的满足感可以用经济学中的“效用”来表示，理性消费者面对一系列商品时，会选择效用最大的商品。

2.项目背景

数据集来自于biogeme官网数据集中的Airline Itinerary数据，这里是数据介绍。总结来说，波音公司进行了一个调查，给乘客提供三个备选项：1.直飞，2.中转但同一公司，3.中转但非同一公司。调查涉及各个备选项的飞行时间、价格、空间等备选项属性，以及乘客本身的收入、受教育程度、出行人数等决策者属性。
我们要做的流程：设计DCM效用函数$\to$用真实数据进行回归$\to$修改DCM效用函数$\to$对结果进行解读。

3.数据预处理

3.1变量的分类

原数据信息如下：

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3609 entries, 0 to 3608
Data columns (total 56 columns):
 #   Column                             Non-Null Count  Dtype  
---  ------                             --------------  -----  
 0   SubjectId                          3609 non-null   int64  
 1   OriginGMT                          3609 non-null   int64  
 2   DestinationGMT                     3609 non-null   int64  
 3   Direction                          3609 non-null   int64  
 4   q02_TripPurpose                    3609 non-null   int64  
 5   q03_WhoPays                        3609 non-null   int64  
 6   q11_DepartureOrArrivalIsImportant  3609 non-null   int64  
 7   q12_IdealDepTime                   3609 non-null   int64  
 8   q13_IdealArrTime                   3609 non-null   int64  
 9   q14_PartySize                      3609 non-null   int64  
 10  q15_Age                            3609 non-null   float64
 11  q16_Income                         3609 non-null   int64  
 12  Cont_Income                        3609 non-null   float64
 13  q17_Gender                         3609 non-null   int64  
 14  q19_Occupation                     3609 non-null   int64  
 15  q20_Education                      3609 non-null   int64  
 16  AirlineFirstFlight_1               3609 non-null   int64  
 17  AirlineFirstFlight_2               3609 non-null   int64  
 18  AirlineFirstFlight_3               3609 non-null   int64  
 19  AirlineSecondFlight_1              3609 non-null   int64  
 20  AirlineSecondFlight_2              3609 non-null   int64  
 21  AirlineSecondFlight_3              3609 non-null   int64  
 22  AirplaneFirstFlight_1              3609 non-null   int64  
 23  AirplaneFirstFlight_2              3609 non-null   int64  
 24  AirplaneFirstFlight_3              3609 non-null   int64  
 25  AirplaneSecondFlight_1             3609 non-null   int64  
 26  AirplaneSecondFlight_2             3609 non-null   int64  
 27  AirplaneSecondFlight_3             3609 non-null   int64  
 28  DepartureTimeHours_1               3609 non-null   float64
 29  DepartureTimeHours_2               3609 non-null   float64
 30  DepartureTimeHours_3               3609 non-null   float64
 31  DepartureTimeMins_1                3609 non-null   int64  
 32  DepartureTimeMins_2                3609 non-null   int64  
 33  DepartureTimeMins_3                3609 non-null   int64  
 34  ArrivalTimeHours_1                 3609 non-null   float64
 35  ArrivalTimeHours_2                 3609 non-null   float64
 36  ArrivalTimeHours_3                 3609 non-null   float64
 37  ArrivalTimeMins_1                  3609 non-null   int64  
 38  ArrivalTimeMins_2                  3609 non-null   int64  
 39  ArrivalTimeMins_3                  3609 non-null   int64  
 40  FlyingTimeHours_1                  3609 non-null   float64
 41  FlyingTimeHours_2                  3609 non-null   float64
 42  FlyingTimeHours_3                  3609 non-null   float64
 43  TripTimeHours_1                    3609 non-null   float64
 44  TripTimeHours_2                    3609 non-null   float64
 45  TripTimeHours_3                    3609 non-null   float64
 46  Legroom_1                          3609 non-null   int64  
 47  Legroom_2                          3609 non-null   int64  
 48  Legroom_3                          3609 non-null   int64  
 49  Fare_1                             3609 non-null   int64  
 50  Fare_2                             3609 non-null   int64  
 51  Fare_3                             3609 non-null   int64  
 52  BestAlternative_1                  3609 non-null   int64  
 53  BestAlternative_2                  3609 non-null   int64  
 54  BestAlternative_3                  3609 non-null   int64  
 55  TripPurpose                        3609 non-null   int64  
dtypes: float64(14), int64(42)
memory usage: 1.5 MB

第0项是id，第1-15包含了决策者的个人信息，为决策者变量；16-51为备选项属性，后面的1、2、3区分三个选项；52-54为0-1型数据，代表是否选择该项。

3.2长宽数据转换

常用的机器学习模型大多使用宽数据，但Logit使用的是长数据，在这里使用pylogit.convert_wide_to_long方法进行宽转长的操作。

#决策者变量
ind_var=['OriginGMT', 'DestinationGMT', 'Direction', 'q02_TripPurpose',
       'q03_WhoPays', 'q11_DepartureOrArrivalIsImportant', 'q12_IdealDepTime',
       'q13_IdealArrTime', 'q14_PartySize', 'q15_Age', 'q16_Income',
       'Cont_Income', 'q17_Gender', 'q19_Occupation', 'q20_Education','TripPurpose']
#备选项属性变量
spv=['AirlineFirstFlight','AirlineSecondFlight','AirplaneFirstFlight','AirplaneSecondFlight',
     'DepartureTimeHours','DepartureTimeMins','ArrivalTimeHours','ArrivalTimeMins','FlyingTimeHours',
    'TripTimeHours','Legroom','Fare']

#备选项对应的字段
alt_varying_var={}
for n in spv:
    dic={}
    for i in 1,2,3:
        dic[i]=n+'_'+str(i)
    alt_varying_var[n]=dic

#选项可用性
avail_var={1:'avil_1',2:'avil_2',3:'avil_3'}

#备选项id
alt_id='ALT_ID'

#观测id
obs_id='OBS_ID'
airline[obs_id]=np.arange(airline.shape[0],dtype=int)+1

#选择结果
choice_id='choice'
long_df=pl.convert_wide_to_long(airline,ind_var,alt_varying_var,avail_var,obs_id,choice_id,new_alt_id_name=alt_id)

3.3数据初筛

当数据特征多且杂时，要在一开始对数据进行初步筛选，这一步要结合数据的信息与个人经验：

• 删掉空值过多的特征。
• 信息高度重合的特征只保留一个。
• 删掉与目标无关联的特征。

除此之外要尽可能保留特征，被删掉的特征也不是被判了“死刑”，后续视情况决定是否恢复。可以用df.info()函数查看数据的格式及空值情况。
最后经过长宽转化、数据清洗及初筛后保留下的结果：

OBS_ID	ALT_ID	Direction	q02_TripPurpose	q03_WhoPays	q11_DepartureOrArrivalIsImportant	q14_PartySize	q15_Age	q16_Income	q20_Education	q17_Gender	q19_Occupation	FlyingTimeHours	DepartureTimeHours	ArrivalTimeHours	TripTimeHours	Legroom	Fare	choice
2	1	1	2	1	2	1	3.5	10	6	1	1	2.53333	7.5	10.0333	2.53333	2	315	0
2	2	1	2	1	2	1	3.5	10	6	1	1	3.03333	15	18.5333	3.53333	2	315	1
2	3	1	2	1	2	1	3.5	10	6	1	1	3.03333	12	16.5333	4.53333	3	350	0
3	1	1	2	1	1	2	3.5	6	6	1	2	2.53333	7.5	10.0333	2.53333	3	195	0
3	2	1	2	1	1	2	3.5	6	6	1	2	3.03333	9	13.5333	4.53333	1	160	1
3	3	1	2	1	1	2	3.5	6	6	1	2	3.03333	12	17.0333	5.03333	4	170	0
4	1	1	2	3	1	2	6	12	6	2	2	0.966667	18	18.9667	0.966667	3	135	0
4	2	1	2	3	1	2	6	12	6	2	2	1.46667	18	21.4667	3.46667	3	125	0
4	3	1	2	3	1	2	6	12	6	2	2	1.46667	12	13.9667	1.96667	1	140	1
6	1	2	4	1	1	1	3.5	7	5	2	5	4.56667	7	14.5667	4.56667	3	400	1
6	2	2	4	1	1	1	3.5	7	5	2	5	5.06667	13	22.0667	6.06667	1	330	0

4.模型构建

4.1单因素分析

简单来说，单因素分析方法就是检验分析一个因素与另外一个因素的关联的分析方法， 单因素分析只观察两个因素间的关联，不代表因果关系 。这里应用单因素分析对特征进行进一步筛选。

方法	应用数据类型	例子
卡方检验	定类和定类	性别和是否戴眼镜之间的关系
t检验、ANOVA	定类和定量	性别和身高的关系
pearson相关系数	定量和定量	身高和体重的关系

除上述方法外，还可以使用单因素回归分析，不同于单因素分析利用传统统计学手段，单因素回归分析是将单个特征和待拟合项纳入我们的回归模型，其效果作为我们筛选特征的依据。
在我们的例子中，因变量是定类的数据，所以选择卡方检验来分析定类的特征，对定量的特征我们直接代入Logit模型进行单因素回归分析。注意这里使用的是宽数据而非最终带入模型的长数据。

卡方分析

##卡方分析
from scipy.stats import chi2_contingency 
import statsmodels.api as sm
from sklearn import metrics
def Disc_var_test(df,col,target):
    p_value=[]
    for n in col:
        crosstab=pd.crosstab(df[n],df[target])
        p=chi2_contingency(crosstab)[1]
        p_value.append(p)
    df=pd.DataFrame({'features':col,'p_value':p_value})
    return df


col=['Direction','q02_TripPurpose','q03_WhoPays','q11_DepartureOrArrivalIsImportant','q17_Gender','q19_Occupation']
Disc_var_test(df_wide,col,'choice')

MNL模型单因素回归分析

import pandas
import statsmodels.api as st#利用MNL模型单因素回归分析
def Mnl_var_test(df,col,target):
    l1,l2,l3,l4=[],[],[],[]
    for n in col:
        mdl = st.MNLogit(df_wide[target],df_wide[n])
        mdl_fit = mdl.fit()
        mdl_margeff = mdl_fit.get_margeff()
        l=list(mdl_margeff.summary_frame()['Pr(>|z|)'])
        l1.append(l[0])
        l2.append(l[1])
        l3.append(l[2])
        l4.append(mdl_fit.aic)
    df=pd.DataFrame({'features':col,'p_value_1':l1,'p_value_2':l2,'p_value_3':l3,'aic':l4})
    return df

col=['q14_PartySize','q15_Age','q16_Income','q20_Education','FlyingTimeHours_1','FlyingTimeHours_2','FlyingTimeHours_3'
      ,'DepartureTimeHours_1','DepartureTimeHours_2','DepartureTimeHours_3'
      ,'ArrivalTimeHours_1','ArrivalTimeHours_2','ArrivalTimeHours_3'
      ,'TripTimeHours_1','TripTimeHours_2','TripTimeHours_3'
      ,'Legroom_1','Legroom_2','Legroom_3'
      ,'Fare_1','Fare_2','Fare_3']
Mnl_var_test(df_wide,col,'choice')

结果汇总

定类数据结果	定量数据结果

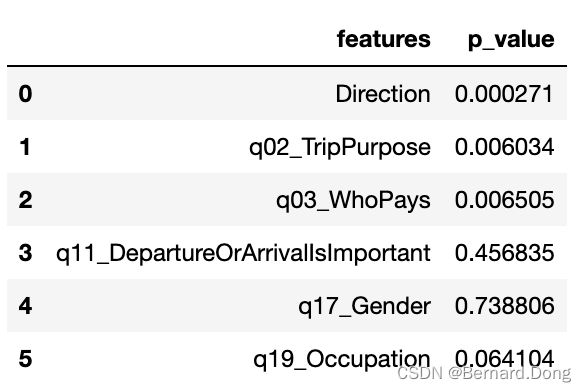剔除p>0.05的特征，即：
q11_DepartureOrArrivalIsImportant q17_Gender q19_Occupation

4.2共线性检测

由于Logit模型是线性模型，变量间严重的多重共线性会影响参数估计的准确性以及泛化能力，所以要对数值型数据进行线性共线性检测。这里使用variance indlation factor（方差膨胀因子）进行评估：
VIF的一般标准为：

• 当0
• 当5
• 当10
• 当VIF>100，严重共线性。

在这里处理vif大于10的特征，保留单变量分析中aic最小的变量。

在这里插入代码片from statsmodels.stats.outliers_influence import variance_inflation_factor
X=df_wide[['q14_PartySize','q15_Age','q16_Income','q20_Education','FlyingTimeHours_1','FlyingTimeHours_2','FlyingTimeHours_3'
      ,'DepartureTimeHours_1','DepartureTimeHours_2','DepartureTimeHours_3'
      ,'ArrivalTimeHours_1','ArrivalTimeHours_2','ArrivalTimeHours_3'
      ,'TripTimeHours_1','TripTimeHours_2','TripTimeHours_3'
      ,'Legroom_1','Legroom_2','Legroom_3'
      ,'Fare_1','Fare_2','Fare_3']]
vif=pd.DataFrame()
vif['VIF Factor']=[variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
vif['features']=X.columns
print(vif)

剔除共线性前

      VIF Factor              features
0   4.197024e+00         q14_PartySize
1   1.538147e+01               q15_Age
2   8.150309e+00            q16_Income
3   1.385489e+01         q20_Education
4            inf     FlyingTimeHours_1
5            inf     FlyingTimeHours_2
6            inf     FlyingTimeHours_3
7   6.470689e+12  DepartureTimeHours_1
8   2.144571e+13  DepartureTimeHours_2
9   2.180920e+13  DepartureTimeHours_3
10  1.235555e+13    ArrivalTimeHours_1
11  5.060224e+13    ArrivalTimeHours_2
12  5.146971e+13    ArrivalTimeHours_3
13           inf       TripTimeHours_1
14  4.370305e+12       TripTimeHours_2
15  4.419627e+12       TripTimeHours_3
16  5.904812e+00             Legroom_1
17  5.905125e+00             Legroom_2
18  6.059211e+00             Legroom_3
19  5.584576e+01                Fare_1
20  5.883837e+01                Fare_2
21  5.442192e+01                Fare_3

剔除共线性后

   VIF Factor           features
0    3.900565      q14_PartySize
1    5.741539         q16_Income
2    9.107147  FlyingTimeHours_1
3    5.134774          Legroom_1
4    4.759455          Legroom_2
5    4.844795          Legroom_3
6    7.644040             Fare_1

4.3哑变量处理

对于三值以上的离散变量要进行哑变量处理

from sklearn.preprocessing import OneHotEncoder
col=['Direction','q02_TripPurpose','q03_WhoPays']
col1=['Direction','q02_TripPurpose','q03_WhoPays']
col2=['q14_PartySize','q16_Income']
col3=['OBS_ID','ALT_ID','TripTimeHours','Legroom','Fare','choice']
df_long=clean(long_df,col1,col2,col3)
# #将值作映射
def make_dummy(df,col):
    encode = pd.get_dummies(df[col])
    df=df.drop(col,1)
    df=pd.concat([df,encode],axis=1)
    return df
data=make_dummy(df_long,col)

4.4模型训练

MNL模型需要满足IIA假设，即无关选择独立性假设。具体来说对于任何决策者，选择两个备选项的概率之比与其他选项的存在无关。换句话说，选项之间不能有明显的从属关系，但在我们的例子中，选项二和选项三都有中转行为，明显区别于选项一，所以我们使用NL嵌套Logit模型代替MNL。

from collections import OrderedDict
User=['Direction_1', 'Direction_2', 'q02_TripPurpose_1',
       'q02_TripPurpose_2', 'q02_TripPurpose_3', 'q02_TripPurpose_4',
       'q03_WhoPays_1', 'q03_WhoPays_2', 'q03_WhoPays_3','q14_PartySize', 'q16_Income']
# User=[]
Dicision=['Legroom','Fare']
Features=User+Dicision

nest,basic_spec,basic_name=OrderedDict(),OrderedDict(),OrderedDict()
nest['one_flight']=[1]
nest['two_flight']=[2,3]

basic_spec['intercept']=[1,2,3]
basic_name['intercept']=['ASC_1','ASC_2','ASC_3']

for n in User:
    basic_name[n]=[n]
    basic_spec[n]=[[1,2,3]]

for n in Dicision:
    basic_name[n]=[n+'_'+str(i) for i in range(1,4)]
#     basic_name[n]=[n]
    basic_spec[n]=[1,2,3]
    
mnl=pl.create_choice_model(
    data=data,
    alt_id_col='ALT_ID',
    obs_id_col='OBS_ID',
    choice_col='choice',
    specification=basic_spec,
    model_type='Nested Logit',
    names=basic_name,
    nest_spec=nest
)
mnl.fit_mle(np.zeros(22))
mnl.get_statsmodels_summary()

5.结果

Dep. Variable:	choice	No. Observations:	1,761
Model:	Nested Logit Model	Df Residuals:	1,739
Method:	MLE	Df Model:	22
Date:	Thu, 16 Jun 2022	Pseudo R-squ.:	0.358
Time:	21:18:13	Pseudo R-bar-squ.:	0.346
AIC:	2,260.567	Log-Likelihood:	-1,108.283
BIC:	2,380.987	LL-Null:	-1,727.465

	coef	std err	z	p_value	[0.025	0.975]
one_flight	0	nan	nan	nan	nan	nan
two_flight	0.3720	0.254	1.466	0.143	-0.125	0.869
ASC_1	0.6701	nan	nan	nan	nan	nan
ASC_2	-0.2182	nan	nan	nan	nan	nan
ASC_3	-0.4519	nan	nan	nan	nan	nan
Direction_1	-2.395e-13	4.17e+21	-5.74e-35	1.000	-8.18e+21	8.18e+21
Direction_2	-1.131e-12	4.21e+21	-2.68e-34	1.000	-8.26e+21	8.26e+21
q02_TripPurpose_1	-2.475e-13	nan	nan	nan	nan	nan
q02_TripPurpose_2	-1.024e-12	nan	nan	nan	nan	nan
q02_TripPurpose_3	-1.863e-14	nan	nan	nan	nan	nan
q02_TripPurpose_4	-7.025e-14	nan	nan	nan	nan	nan
q03_WhoPays_1	-1.109e-12	nan	nan	nan	nan	nan
q03_WhoPays_2	-1.833e-13	nan	nan	nan	nan	nan
q03_WhoPays_3	-2.636e-14	nan	nan	nan	nan	nan
q14_PartySize	-2.206e-12	2.09e+14	-1.06e-26	1.000	-4.09e+14	4.09e+14
q16_Income	-1.147e-11	4.32e+13	-2.66e-25	1.000	-8.46e+13	8.46e+13
Legroom_1	0.1991	0.053	3.733	0.000	0.095	0.304
Legroom_2	0.1185	0.053	2.238	0.025	0.015	0.222
Legroom_3	0.1448	0.054	2.692	0.007	0.039	0.250
Fare_1	-0.0177	0.001	-15.623	0.000	-0.020	-0.015
Fare_2	-0.0201	0.001	-14.779	0.000	-0.023	-0.017
Fare_3	-0.0192	0.001	-14.381	0.000	-0.022	-0.017
TripTimeHours_1	-0.4809	0.095	-5.051	0.000	-0.668	-0.294
TripTimeHours_2	-0.2588	0.083	-3.130	0.002	-0.421	-0.097
TripTimeHours_3	-0.3010	0.083	-3.617	0.000	-0.464	-0.138

我们发现虽然前面做了那么多分析，从结果来看真正显著的项只有Legroom Fare TripTime，即座位空间、票价和旅行时间，与选择者本人的属性如收入、旅行人数等都无关联。
从系数来看，其中影响程度最大的为旅行时间，其次是座位空间，票价反倒影响不那么大。其中的缘由可能就是统计学实验中的选择性偏差吧，飞机属于较昂贵的出行方式，购买机票的群体本身对价格并不十分敏感，更看重飞行体验。
完整代码及数据