PyTorch深度学习 学习记录6_2

1x1的卷积核

1x1的卷积核的主要目的是为了降维，在面对大量数据的时候运算量往往会变得非常大，那么1x1的卷积核能对数据进行处理，将维度降下来：
像如上运算将三个通道降维了一个通道。经过这种处理我们在整个数据集上就会有一个显著的提升：
在我们是由1x1的卷积核以后尽管网络变得复杂了但是计算量缺少了一个量级，大幅降低了我们的计算时间。
详情可见这里

GoogleNet

以上的网络就是GoogleNet是现在常见的一种网络架构，虽然看着很恐怖但其中有很多和红圈中一样的重复的模块，这个模块称为为Inception，具体情况如下：

其中的网络是并行处理的，我们把数据丢进去同时在多个网络中进行训练，哪个网络训练的好就赋予该网络更多的权重，就是做这样简单的事情，其模块的代码为：

import torch
import torch.nn
import torch.nn.functional as F
class InceptionA(torch.nn.Module):
    def __init__(self,in_channels):
        super(InceptionA,self).__init__()
        
        self.branch1x1=nn.Conv2d(in_channels,16,kernel_size=1)
        
        self.branch5x5_1=nn.Conv2d(in_channels,16,kernel_size=1)
        self.branch5x5_2=nn.Conv2d(16,24,kernel_size=5,padding=2)
        
        self.branch3x3_1=nn.Conv2d(in_channels,16,kernel_size=1)
        self.branch3x3_2=nn.Conv2d(16,24,kernel_size=3,padding=1)
        self.branch3x3_3=nn.Conv2d(24,24,kernel_size=3,padding=1)
        
        self.branch_pool=nn.Conv2d(in_channels,24,kernel_size=1)
        
    def forward(self,x):
        branch1x1=self.branch1x1(x)
        
        branch5x5=self.branch5x5_1(x)
        branch5x5=self.branch5x5_2(branch5x5)
        
        branch3x3=self.branch3x3_1(x)
        branch3x3=self.branch3x3_2(branch3x3)
        branch3x3=self.branch3x3_3(branch3x3)
        
        branch_pool=F.avg_pool2d(x,kernel_size=3,stride=1,padding=1)
        branch_pool=self.branch_pool(branch_pool)
        
        outputs=[branch1x1,branch5x5,branch3x3,branch_pool]
        return torch.cat(outputs,dim=1)#把channel的维度拼起来

还是使用MNIST数据集我们简单做一个网络：

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv1=nn.Conv2d(1,10,kernel_size=5)
        self.conv2=nn.Conv2d(88,20,kernel_size=5)
        
        self.incep1=InceptionA(in_channels=10)
        self.incep2=InceptionA(in_channels=20)
        
        self.mp=nn.MaxPool2d(2)
        self.fc=nn.Linear(1408,10)
        
    def forward(self,x):
        in_size=x.size(0)
        x=F.relu(self.mp(self.conv1(x)))
        x=self.incep1(x)
        x=F.relu(self.mp(self.conv2(x)))
        x=self.incep2(x)
        x=x.view(in_size,-1)
        x=self.fc(x)
        return x

梯度消失

通常会认为将网络越叠越深我们会不断提高网络的性能，但实际上并不会这样：
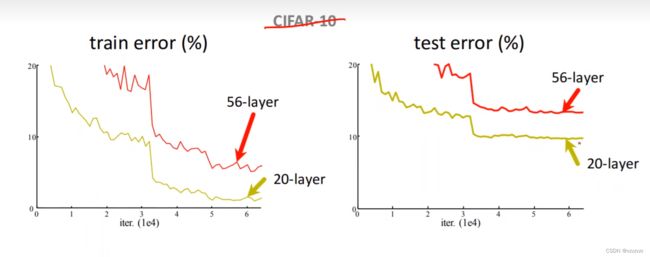我们能看到56层的网络远不如20层的网络，过高的层数意味着我们的反向传播会变得很长，链式法则是通过相乘进行运算的，也就是说我们反向传播的过程中有许多小于1的数最终的结果会变得可以忽略不记，在计算机中甚至可能会由于精度问题直接下溢，这种情况被称为梯度消失。为了解决这个问题我们引入residual net（残差网络）

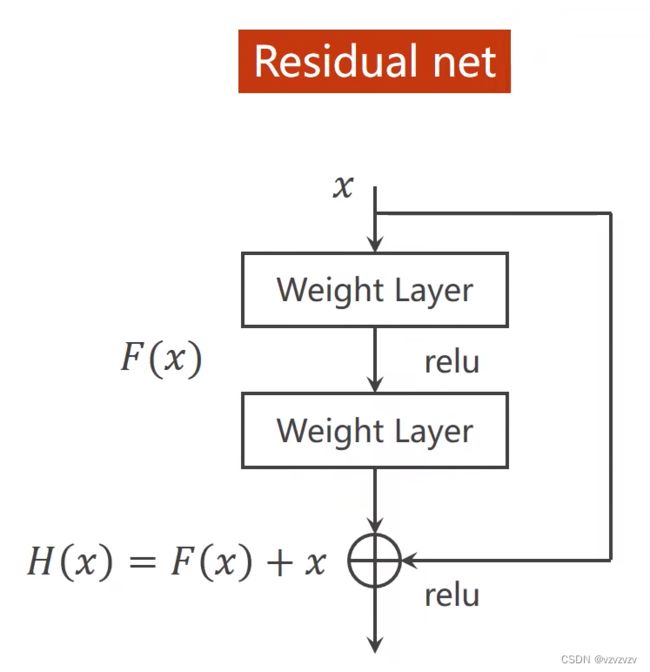
在激活之前我们将H(X)对X求导$$\frac{\partial H(x)}{\partial x}=\frac{\partial F(x)}{\partial x}+1$$那么即使发生梯度消失最终的值也会在1附近，这样我们就可以对比较前面的层进行更好的学习。
代码块：

class ResidualBlock(nn.Module):
    def __init__(self,channels):
        super(ResidualBlock,self).__init__()
        self.channels=channels
        self.conv1=nn.Conv2d(channels,channels,kernel_size=3,padding=1)#保证输入输出的通道数不变
        self.conv2=nn.Conv2d(channels,channels,kernel_size=3,padding=1)
        
    def forward(self,x):
        y=F.relu(self.conv1(x))
        y=self.conv2(y)#在激活之前
        return F.relu(y+x)
    
class Net(nn.Module):
    def __init__(self):
        super(Net2,self).__init__()
        self.conv1=nn.Conv2d(1,16,kernel_size=5)
        self.conv2=nn.Conv2d(16,32,kernel_size=5)
        self.mp=nn.MaxPool2d(2)
        
        self.rcblock1=ResidualBlock(16)
        self.rcblock2=ResidualBlock(32)
        
        self.fc=nn.Linear(512,10)
        
    def forward(self,x):
        batch_size=x.size(0)
        x=self.mp(F.relu(self.conv1(x)))
        x=self.rcblock1(x)
        x=self.mp(F.relu(self.conv2(x)))
        x=self.rcblock2(x)
        x=x.view(batch_size,-1)
        print(x.size(1))
        x=self.fc(x)
        return x