边缘检测方法 -- 一阶边缘检测

目录

摘要

一阶边缘检测基础算子（First Order Edge Detection）

改进的一阶边缘检测

Rorberts交叉算子

Prewitt边缘检测算子 

Sobel检测算子：

---

一阶边缘检测（First Order Edge Detection）

摘要

基于边缘检测的分析不易受整体光照强度变化的影响，边缘检测强调的是图像对比度，即亮度上的差别。要检测边缘位置，我们首先可以应用一阶微分，因为一阶微分可以使变化增强；而当信号没有变化时，一阶微分不会有响应。

一阶边缘检测基础算子（First Order Edge Detection）

定义垂直边缘：（E是edge的缩写）

定义水平边缘：

则垂直和水平边缘：（垂直边缘和水平边缘相加）

                                                

叫做一阶边缘检测。

模板为：

伪代码：

function edge = basic_difference(inage)

for x = 1:cols-2 
    for y = 1:rows-2
        edge(y,x)=abs(2*image(y,x)-image(y+1,x)-image(y+1,x))
    end
end

-------------------------------------------------------------------------------------------------------------------------------- 

改进的一阶边缘检测

泰勒级数分析表明对相邻点的差分处理可以用来估算点的一阶导数

                

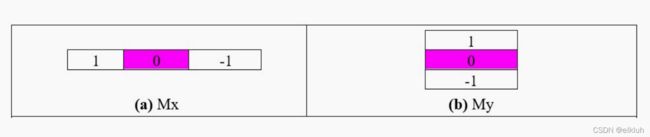
 因此改进的一阶差分模板为：

 Mx为垂直模板，My为水平模板。

 所以改进后的公式为

---------------------------------------------------------------------------------------------------------------------------------

Rorberts交叉算子

是最早的边缘检测算子之一，它实现的是边缘检测，利用两个模板，计算对角线上而不是沿坐标轴的微分。这两个模板分别为：

 边缘点Ex,y是在图像点Px,y对这两个模板进行卷积计算得到的两个值中的较大值，公式为：

 Roberts交叉算子的应用：

--------------------------------------------------------------------------------------------------------------------------------

Prewitt边缘检测算子 

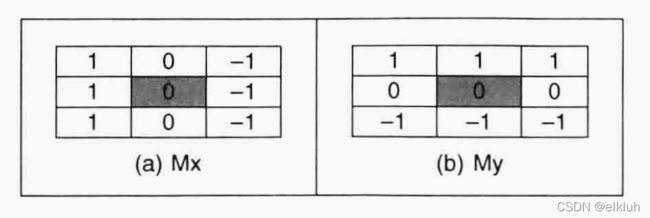
Prewitt算子模板为： 

 其中Mx是垂直模板，My是水平模板。

对于垂直模板，首先（a）图中最中间阴影部分是我们要求的像素值。它等于它周围的8个像素值做卷积得到，也就是Mx与这九个像素值做内积，像素 P_00 * 1 + P_01 * 0 + P_02 * (-1) + P_10 * 1 + P_11 * 0 + P_12 * (-1) + P_20 * 1 + P_21 * 0 + P_22 * (-1)。 得到Mx(x,y)。（这个符号我也没有看懂代表啥）

对于水平模板，首先（b）图中最中间阴影部分是我们要求的像素值。它等于它周围的8个像素值做卷积得到，也就是Mx与这九个像素值做内积，像素 P_00 * 1 + P_01 * 1 + P_02 * 1 + P_10 * 0 + P_11 * 0 + P_12 * 0 + P_20 * (-1) + P_21 * (-1) + P_22 * (-1)。 

然后把Mx(x,y) , My(x,y)的平方和开方得到我们阴影部分就是最中心的那个像素值。这是矢量的求法，（类似于求三角形形的斜边）如下面的式子所示。

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

边缘强度M表示的是矢量的长度，边缘方向θ表示的是矢量的方向。

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

Matlab代码

image=double(imread('lizardsmall.png'));
[rows, cols]=size(image)
edge = zeros(rows,cols)
kernelx = [1,0,-1;1,0,-1;1,0,-1]
kernely = [1,1,1;0,0,0;-1,-1,-1]
for x = 2:cols-1 
    for y = 2:rows-1
        tempx = sum(sum(image(y-1:y+1,x-1:x+1) * kernelx,1),2);
        tempy = sum(sum(image(y-1:y+1,x-1:x+1) * kernely,1),2);
        edge(y,x)=abs(sqrt(tempx*tempx+tempy*tempy));
    end
end
imshow(uint8(edge)),title('original');

---

 

Sobel检测算子：

Prewitt算子模板为：

 Sobel算子的每个像素的计算公式和Prewitt相同，就是前面的系数变了。

参考书籍 《Feature extraction and image processing》 Mark S. Nixon and Alberto S. Aguado 

中文版，《特征提取与图像处理》