基于朴素贝叶斯的鸢尾花数据集分类

1.作者介绍

王炜鑫，男，西安工程大学电子信息学院，2021级研究生
研究方向：小型无人直升机模型辨识
电子邮件：[email protected]

刘帅波，男，西安工程大学电子信息学院，2021级研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：[email protected]

2.理论知识介绍

2.1算法介绍

Naive Bayes算法，又叫朴素贝叶斯算法，朴素：特征条件独立；贝叶斯：基于贝叶斯定理。属于监督学习的生成模型，实现简单，没有迭代，并有坚实的数学理论（即贝叶斯定理）作为支撑。在大量样本下会有较好的表现，不适用于输入向量的特征条件有关联的场景。
朴素贝叶斯的过程主要分为两个阶段。第一阶段，对实验样本进行分类，分别计算不同条件下其概率。第二阶段，输入测试样本，计算不同条件其概率，比较其概率大小，从而完成对测试样本的分类。下图显示两类实验样本的概率分布情况。

实现样本的分类，需要通过计算条件概率而得到，计算条件概率的方法称为贝叶斯准则。条件概率的计算方法：

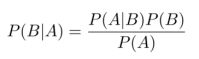
其中P(A|B)代表条件B下，结果A发生的概率，P(B|A)代表条件A下，结果B发生的概率，P(B)代表条件B发生的概率，P(A)代表条件A发生的概率。
当条件与结果发生交换，计算P(B|A)的方法，在已知 P(A|B)，P(B)，P(A)的情况下可由如上公式得到。
朴素贝叶斯分类器，其核心方法是通过使用条件概率来实现分类。应用贝叶斯准则可以得：

其中P(ci|x,y)代表中给定某个由x、y表示的数据点，该数据点属于类别 ci 的概率。 而朴素贝叶斯分类器基于一个简单的假定：给定目标值时属性之间相互条件独立。即P(x,y|ci)（i=1,2,3……n）相互独立，互不影响。通过贝叶斯准则，定义贝叶斯分类准则为：如果P(c1|x,y)>P(c2|x,y)，那么属于类别c1; 如果P(c2|x,y)> P(c1|x,y)，那么属于类别 c2;
朴素贝叶斯分类器具体步骤如下：
（1）输入训练样本，统计特征。
（2）完成训练样本的向量化。
（3）计算各个特征的条件概率。
（4）输入测试样本
（5）根据测试样本中提供的特征，计算不同类别的条件概率。
（6）根据最大条件概率，完成测试样本分类。

2.2数据集介绍

iris数据集：数据集包含150个样本，对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息，所以iris数据集是一个150行5列的二维表。通俗地说，iris数据集是用来给花做分类的数据集，每个样本包含了sepal_length(花萼长度)、sepal_width(花萼宽度)、petal_length(花瓣长度)、petal_width(花瓣宽度)四个特征（前4列），我们需要建立一个分类器，分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾（这三个名词都是花的品种）。下图是样本局部截图：

3.实验代码及结果

3.1 数据集下载

iris数据集下载地址：http://download.tensorflow.org/data/iris_training.csv，下载后重命名为iris.csv，并保存到代码所在文件夹
注意：复制上面网址粘贴到网页空白页，按回车键即可下载该数据集

3.2实验代码

#导入数据分析所需要的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

data = pd.read_csv('iris.csv',header=None)
x = data.drop([4],axis=1)
x = x.drop([0],axis=0)
x = np.array(x,dtype=float)
print(x)
y=pd.Categorical(data[4]).codes
print(data[4])
y=y[1:151]
print(y)
p=x[:,2:5]

x_train1,x_test1,y_train1,y_test1=train_test_split(x,y,train_size=0.8,random_state=14)
x_train,x_test,y_train,y_test=x_train1,x_test1,y_train1,y_test1
print('训练数据集样本数目：%d，测试数据集样本数目：%d'%(x_train.shape[0],x_test.shape[0]))
clf=GaussianNB()
ir=clf.fit(x_train,y_train)
y_pred=ir.predict(x_test)
acc = np.sum(y_test == y_pred)/x_test.shape[0]
print('测试集准确度：%.3f'% acc)
y_pred = ir.predict(x_train)
acc = np.sum(y_train == y_pred)/x_train.shape[0]
print('训练集准确度：%.3f'% acc)

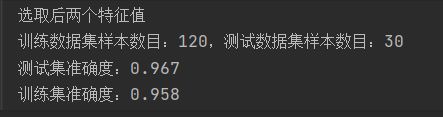
print('选取前两个特征值')
p=x[:,:2]
p_train1,p_test1,y_train1,y_test1=train_test_split(p,y,train_size=0.8,random_state=1)
p_train,p_test,y_train,y_test=p_train1,p_test1,y_train1,y_test1
print('训练数据集样本数目：%d，测试数据集样本数目：%d'%(p_train.shape[0],p_test.shape[0]))
clf=GaussianNB()
ir=clf.fit(p_train,y_train)
y_pred=ir.predict(p_test)
acc = np.sum(y_test == y_pred)/p_test.shape[0]
print('测试集准确度：%.3f'% acc)
y_pred = ir.predict(p_train)
acc = np.sum(y_train == y_pred)/p_train.shape[0]
print('训练集准确度：%.3f'% acc)

p1_max,p1_min = max(p_test[:,0]),min(p_test[:,0])
p2_max,p2_min = max(p_test[:,1]),min(p_test[:,1])
t1 = np.linspace(p1_min,p1_max,500)
t2 = np.linspace(p2_min,p2_max,500)
p1,p2 = np.meshgrid(t1,t2)#生成网格采样点
p_test1 = np.stack((p1.flat, p2.flat), axis=1)
y_hat = ir.predict(p_test1)
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.figure(facecolor='w')
plt.pcolormesh(p1, p2, y_hat.reshape(p1.shape),shading='auto', cmap=cm_light) # 预测值的显示
plt.scatter(p_test[:, 0], p_test[:, 1], c=y_test, edgecolors='k', s=50, cmap=cm_dark)  # 样本
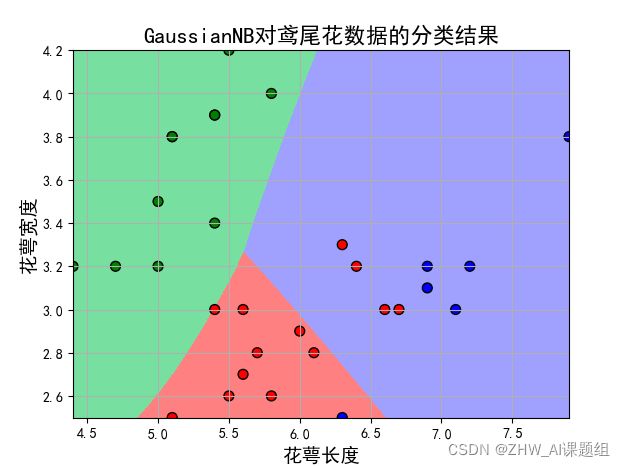
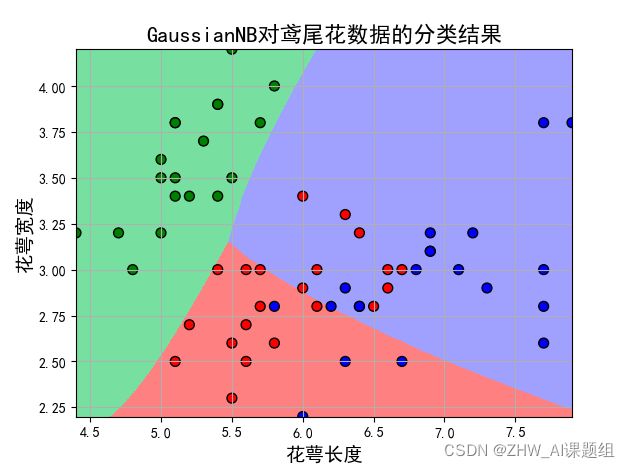
plt.xlabel(u'花萼长度', fontsize=14)
plt.ylabel(u'花萼宽度', fontsize=14)
plt.title(u'GaussianNB对鸢尾花数据的分类结果', fontsize=16)
plt.grid(True)
plt.xlim(p1_min, p1_max)
plt.ylim(p2_min, p2_max)
plt.show()

print('选取后两个特征值')
q=x[:,2:4]
q_train1,q_test1,y_train1,y_test1=train_test_split(q,y,train_size=0.8,random_state=1)
q_train,q_test,y_train,y_test=q_train1,q_test1,y_train1,y_test1
print('训练数据集样本数目：%d，测试数据集样本数目：%d'%(q_train.shape[0],q_test.shape[0]))
clf=GaussianNB()
ir=clf.fit(q_train,y_train)
y_pred=ir.predict(q_test)
acc = np.sum(y_test == y_pred)/q_test.shape[0]
print('测试集准确度：%.3f'% acc)
y_pred = ir.predict(q_train)
acc = np.sum(y_train == y_pred)/q_train.shape[0]
print('训练集准确度：%.3f'% acc)

q1_max,q1_min = max(q_test[:,0]),min(q_test[:,0])
q2_max,q2_min = max(q_test[:,1]),min(q_test[:,1])
t1 = np.linspace(q1_min,q1_max,500)
t2 = np.linspace(q2_min,q2_max,500)
q1,q2 = np.meshgrid(t1,t2)#生成网格采样点
q_test1 = np.stack((q1.flat, q2.flat), axis=1)
y_hat = ir.predict(q_test1)
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.figure(facecolor='w')
plt.pcolormesh(q1, q2, y_hat.reshape(q1.shape),shading='auto', cmap = cm_light) # 预测值的显示
plt.scatter(q_test[:, 0], q_test[:, 1], c=y_test, edgecolors='k', s=50, cmap= cm_dark)  # 样本
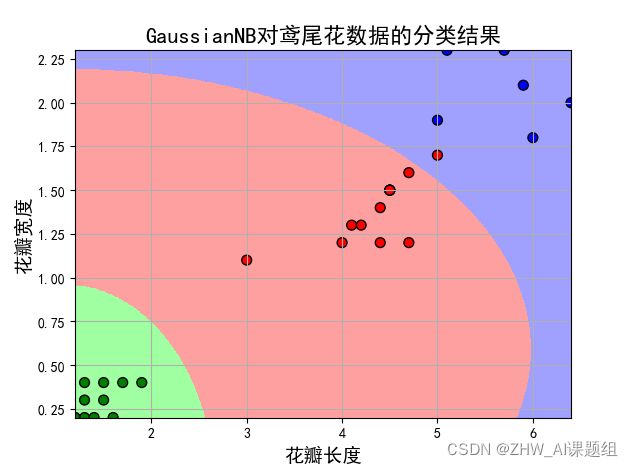
plt.xlabel(u'花瓣长度', fontsize=14)
plt.ylabel(u'花瓣宽度', fontsize=14)
plt.title(u'GaussianNB对鸢尾花数据的分类结果', fontsize=16)
plt.grid(True)
plt.xlim(q1_min, q1_max)
plt.ylim(q2_min, q2_max)
plt.show()

3.2实验结果

(1)取前两个特征值：

(2)取后两个特征值：

改变训练集大小为train_size=0.6

(3)取前两个特征值：

(4)取后两个特征值：


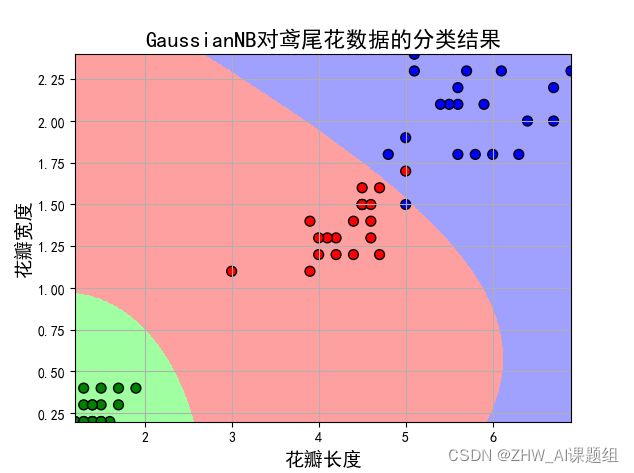
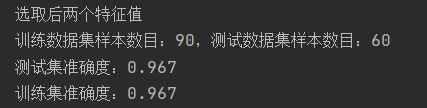
分析：改变训练集与测试集比例后，经过对比分析发现，前两个特征值对检测结果的误差更大，后两个特征值更适合进行分类。训练样本与测试样本之间的比重也会在很大程度上影响到测试误差。