Pytorch中的卷积、空洞卷积和组卷积
Pytorch中的卷积、空洞卷积和组卷积
- 标准卷积Conv2d
-
- 具体操作
- 空洞卷积
- 组卷积
- 参考文献
标准卷积Conv2d
最基础的卷积。下面图虽然丑了点,但足够说明问题了。
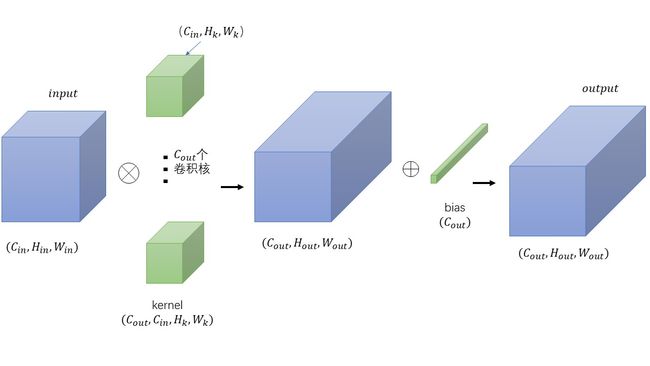
注:
(1) kernel的值在初始化中是随机生成的,可以每个值之间都不一样。
(2)每个通道只对应一个bias值。
具体操作
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
x = torch.rand([1,10,7,7])
a = torch.nn.Conv2d(10,20,1)
y = a(x)
I n p u t : ( N , C i n , H i n , W i n ) O u t p u t : ( N , C o u t , H o u t , W o u t ) Input:(N, C_{in}, H_{in}, W_{in}) \\ Output:(N, C_{out}, H_{out}, W_{out}) Input:(N,Cin,Hin,Win)Output:(N,Cout,Hout,Wout)
H o u t = ⌊ H i n + 2 × padding [ 0 ] − dilation [ 0 ] × ( kernel_size [ 0 ] − 1 ) − 1 stride [ 0 ] + 1 ⌋ H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{padding}[0] - \text{dilation}[0] \times (\text{kernel\_size}[0] - 1) - 1}{\text{stride}[0]} + 1\right\rfloor Hout=⌊stride[0]Hin+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1+1⌋
W o u t = ⌊ W i n + 2 × padding [ 1 ] − dilation [ 1 ] × ( kernel_size [ 1 ] − 1 ) − 1 stride [ 1 ] + 1 ⌋ W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{padding}[1] - \text{dilation}[1] \times (\text{kernel\_size}[1] - 1) - 1}{\text{stride}[1]} + 1\right\rfloor Wout=⌊stride[1]Win+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1+1⌋
注意:
(1)如果把dilation=1带入,就是最基础的公式。
(2)输出的H和W都会向下取整
空洞卷积
通过torch.nn.Conv2d实现,设置不同的dilation。
作用是(1)用于扩大感受野。(2)不同的空洞率可以生成不同尺度的感受野。也就是可以通过不同空洞率来完成多尺度。这对于语义分割很有帮助。
缺点也很明显,跳过了一些信息。
先来一张示意图(图来自于网络)。
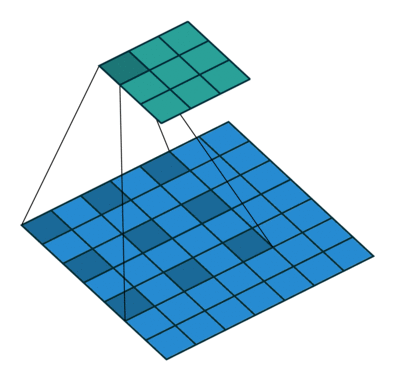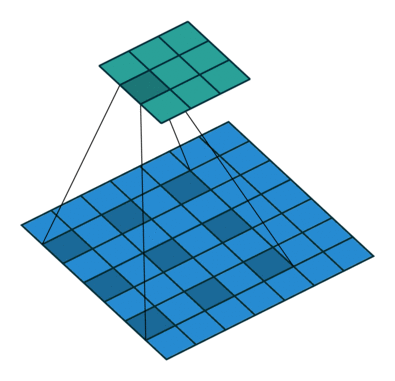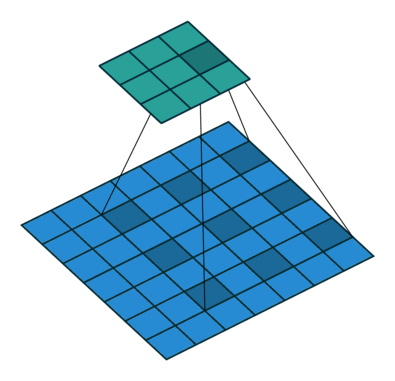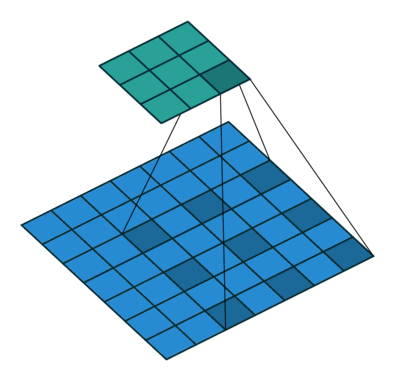
上图表明:当kernel_size=3时,如果将dilation=2,就可以获得相当于kernel_size=5的感受野效果。dilation=3,相当于kernel_size=7。。。通过上面的公式计算,也可以验证。
关于dilation的值可以这么理解,(dilation-1)就是两个卷积核的点之间插入的空格数。
上图中卷积核中两个值的空余部分,可以是0。Pytorch中如何实现有待考证。
组卷积
通过torch.nn.Conv2d实现,设置不同的groups。
-
groups = 1(默认值),就如同普通的卷积
-
groups = 2 分组卷积 ,相当于有两个卷积层,每一层的输入为原来输入通道数的一半,输出也为原来输出的一半,然后再连接:
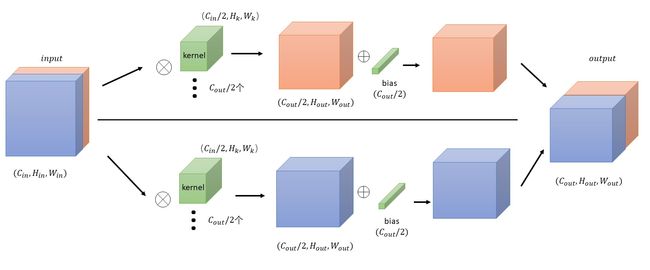
x = torch.ones([1,10,7,7]) a1 = torch.nn.Conv2d(10,20,3,groups=2,bias=False) # 对权重强行赋值,前半部分全为0,后半部分全为1 a1.weight.data[0:10,...] = torch.zeros([10,5,3,3]) a1.weight.data[10:,...] = torch.ones([10,5,3,3]) # 查看y的值,发现前10个通道的值均为0,后10个通道的值均为45 y = a1(x)当group=3,4,…时,可按相同思路考虑。
-
深度卷积depthwise,此时group=in_channels,也就是对每一个输入的通道分别用不同的卷积核卷积。out_channels必须是in_channels的整数倍。
o u t _ c h a n n e l s i n _ c h a n n e l s = k \frac{{out\_channels}}{{in\_channels}} = k in_channelsout_channels=k可以这样理解:
假设torch.nn.Conv2d(in_channels=10,out_channels=20,kernel_size=3,groups=10),input的第0个通道的值负责生成output的第0,1通道的值,input的第1个通道的值负责生成output的第2,3通道的值,以此类推。类似的,当k = 1时,out_channels = in_channels,每一个卷积核分别和每一个输入的通道进行卷积,最后在concat起来。
参考文献
- https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
- https://pytorch.org/docs/1.4.0/