吴恩达机器学习课后习题(学习曲线)
一、学习曲线
实现回归算法后,需要根据拟合数据的情况进行修改算法,增加训练集的数量、增加训练集特征、或改变lambda的大小。本次使用线性回归对计算出的函数曲线进行尽力拟合。
二、实现学习曲线
导入数据包。
import numpy as np
import pandas as pd
import scipy.io as sio
import scipy.optimize as opt
import matplotlib.pyplot as plt
导入数据,并赋值各个变量为数据集,将其初始化。
画出散点图。
data = sio.loadmat("E:\\Pycharm\\workspace\\ex_Andrew\\ex5_Andrew\\ex5data1.mat")
X,y,Xval,yval,Xtest,ytest = map(np.ravel,[data['X'],data['y'],data['Xval'],data['yval'],data['Xtest'],data['ytest']])
#初始化X与y的各个值,map函数为映射函数,将数据集中的数据按分类都转换成一维的数据
#以上数据的shape分别为 (12,), (12,), (21,), (21,), (21,), (21,)。其中各个数据集的数据无关联
fig,ax = plt.subplots(figsize=(8,6))
ax.scatter(X,y)
ax.set_xlabel('water_level')
ax.set_ylabel('flow')
X, Xval, Xtest = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]
theta = np.ones(X.shape[1])
#X,Xval,Xtest的shape都重构为(12,2)(21,2)(21,2),增加一列1。theta的shape为(2,)
定义代价函数、正则化代价函数、梯度函数。
def cost(theta, X, y): #未正则化的代价计算函数
m = X.shape[0]
inner = X @ theta - y
square_sum = inner.T @ inner
cost = square_sum / (2 * m)
return cost
def costReg(theta, X, y, reg):
m = X.shape[0]
inner = X @ theta - y #@运算符为矩阵运算符号
square_sum = inner.T @ inner #线性回归的代价计算
cost = square_sum / (2 * m)
regularized_term = (reg / (2 * m)) * np.power(theta[1:], 2).sum() #正则项计算
return cost + regularized_term
print("初始代价为:",costReg(theta,X,y,1))
def gradient_Reg(theta,X,y,learningrate):
m = X.shape[0]
inner = X.T@(X@theta-y)/(m)
reg_term = theta
reg_term[0] = 0
reg_term = (learningrate*reg_term)/m
return inner+reg_term
print("初始的梯度为:",gradient_Reg(theta,X,y,1))
对初始值使用高级优化算法计算theta值,画出曲线(线性回归拟合程度差)。
fmin = opt.minimize(fun=costReg,x0=theta,jac=gradient_Reg,args=(X,y,0),method='TNC',options={'disp':False})
#options参数:可以是maxiter:int。 要执行的最大迭代数。也可以是disp:布尔型。 设置为True可打印聚合消息(看不懂)。
print("优化函数处理后的梯度为:",fmin.x)
plt.plot(X[:,1],X[:,1]*fmin.x[1]+fmin.x[0],c='b',label='prediction') #plt函数画出直线
设计线性回归函数,用于计算theta。
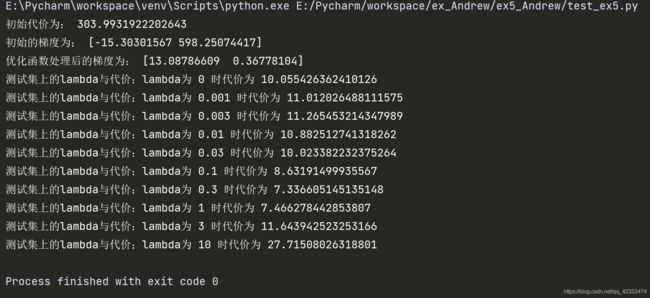
以训练集大小作为横坐标,计算出训练集中不同大小的代价与交叉验证集的代价。
画出学习曲线(训练集代价、交叉验证机代价)
def linear_regression(X,y,learningrate=1): #学习算法,返回优化后的值,向量为res.x
theta = np.ones(X.shape[1])
res = opt.minimize(fun=costReg,x0=theta,jac=gradient_Reg,args=(X,y,learningrate),method='TNC',options={'disp':False})
return res
training_cost = []
cv_cost = [] #初始化代价
m = X.shape[0] #12
for i in range(1,m+1):
res = linear_regression(X[:i,:],y[:i],0) #从第一行开始递增,第一次循环为第一行数据,每次循环中没有第1行
tc = costReg(res.x,X[:i,:],y[:i],0) #前i行训练集的代价
cv = costReg(res.x,Xval,yval,0) #计算一次cv集的代价,每次执行的res值不同,cv值也不同
training_cost.append(tc) #append为增加维度,而非加法运算
cv_cost.append(cv)
#横轴为m,代表训练集大小不同时(1,2...12)的代价,画出曲线后发现欠拟合,高偏差,需要增加
fig,ax_learn = plt.subplots(figsize=(8,6))
plt.plot(np.arange(1,m+1),training_cost,label='training_cost')
plt.plot(np.arange(1,m+1),cv_cost,label='cv_cost')
plt.legend()
观察学习曲线,该算法欠拟合,选择扩大x的特征。
定义扩大特征值函数、均值化归一函数、执行函数(其中使用前两种函数,并加一列数据1,返回修改好的X数据集)
def poly_features(x, power, as_ndarray=False): #布尔型变量控制打印出的是数据集还是矩阵数据
data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)} #for循环实现x扩大参数,利用乘方运算
df = pd.DataFrame(data)
return df.values if as_ndarray else df #False时打印df数据集,而非数据矩阵
def normalize_feature(df): #均值归一化已经扩容的特征
return df.apply(lambda column:(column-column.mean())/column.std())
def prepare_ploy_data(*args,power):
def prepare(x): #返回扩大好的、归一化后的X矩阵
df = poly_features(x, power) #扩大X为三列数据
ndarr = normalize_feature(df).values
return np.insert(ndarr,0,np.ones(ndarr.shape[0]),axis=1)
return [prepare(x) for x in args] #返回args中的X矩阵
重新赋值数据集中的数据进行下一次测试,将原始数据扩容、均值化归一、增加列数。
data = sio.loadmat("E:\\Pycharm\\workspace\\ex_Andrew\\ex5_Andrew\\ex5data1.mat") #找到最初始的数据
X, y, Xval, yval, Xtest, ytest = map(np.ravel,[data['X'], data['y'], data['Xval'], data['yval'], data['Xtest'], data['ytest']])
X_ploy,Xval_ploy,Xtest_ploy = prepare_ploy_data(X,Xval,Xtest,power=8) #增大特征数到8,再加一列1,得出X_ploy的shape为(12,9)
设计画学习曲线的函数,在其中进行计算不同训练集大小的代价(训练集代价、交叉测试及代价)。画出两个图形,一个为学习曲线,一个为拟合数据曲线。
使用之前重新赋值与初始化好的数据调用函数,lambda分别使用1和100观察后发现都不太能合适地拟合数据。
def plot_learning_curve(X, Xinit, y, Xval, yval, l=0):
training_cost, cv_cost = [], [] #初始化数组保存训练集代价与交叉验证集的代价
m = X.shape[0]
for i in range(1, m + 1):
res = linear_regression(X[:i, :], y[:i], l)
tc = cost(res.x, X[:i, :], y[:i])
cv = cost(res.x, Xval, yval)
training_cost.append(tc)
cv_cost.append(cv)
#ax[0]画出学习曲线,训练集代价过低,过度拟合,高方差
fig, ax = plt.subplots(2, 1, figsize=(6,6))
ax[0].plot(np.arange(1, m + 1), training_cost, label='training cost')
ax[0].plot(np.arange(1, m + 1), cv_cost, label='cv cost')
ax[0].legend()
#拟合数据集X,过度拟合数据
fitx = np.linspace(-50, 50, 100) #(-50,50)之间步长100的横坐标
fitxtmp = prepare_ploy_data(fitx, power=8) #扩容100个数据点,扩容为8个数据并加1数据列
fity = np.dot(fitxtmp[0], linear_regression(X, y, l).x.T) #fitxtmp[0]为返回的数组中的数据,点乘运算结果集的theta
ax[1].plot(fitx, fity, c='r', label='fitcurve') #曲线fity
ax[1].scatter(Xinit, y, c='b', label='initial_Xy') #X数据中的散点图
ax[1].set_xlabel('water_level')
ax[1].set_ylabel('flow')
plot_learning_curve(X_ploy, X, y, Xval_ploy, yval, l=0) #X_ploy 为已经扩容且均值化归一后的数据集
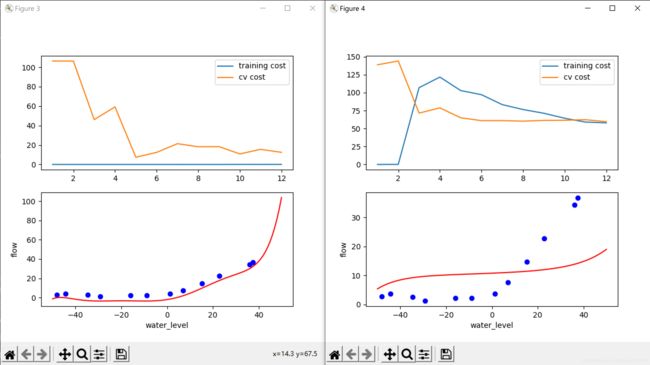
#将l改为100,则出现欠拟合情况,训练集的代价过高
plot_learning_curve(X_ploy, X, y, Xval_ploy, yval, l=100)
初始化几个lambda值,分别算出不同lambda对应的代价(训练集代价、交叉验证集代价)。
画出横坐标为lambda的学习曲线,并打印各个lambda值的代价,从中选择代价最小的即为合适的lambda。
最后打印lambda对应代价是使用的时测试集(Xtest、ytest)。得到的结果与使用不同集而不同。
l_candidate = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost,cv_cost = [],[]
for l in l_candidate:
res = linear_regression(X_ploy,y,l)
tc = cost(res.x,X_ploy,y)
cv = cost(res.x,Xval_ploy,yval)
training_cost.append(tc)
cv_cost.append(cv)
#画出lambda的曲线图,可以看到在3左右值的代价合适
fig,ax = plt.subplots(figsize=(8,6))
ax.plot(l_candidate,training_cost,label='training_cost')
ax.plot(l_candidate,cv_cost,label='cv_cost')
plt.xlabel=('lembda')
plt.ylabel=('cost')
#plt.show()
for l in l_candidate:
theta = linear_regression(X_ploy,y,l).x
print("测试集上的lambda与代价:lambda为",l,"时代价为",cost(theta, Xtest_ploy, ytest))
三、运行结果
初始值使用普通线性回归(直线),拟合数据后根据数据图像与学习曲线观察出此时欠拟合,出现高偏差,此时增加数据数量用处不大。
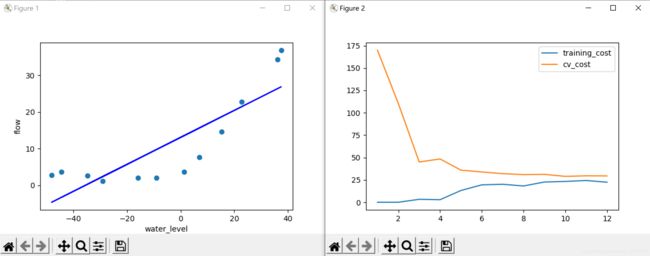
欠拟合状态,可以增加特征数量,或者增加特征多项式的次数。本算法增加多项式特征数量,当lambda值为1时,过度拟合,训练集代价太低几乎不变,故选择提高lambda的值;
当lambda值为100时,欠拟合,训练集和交叉训练集代价都不低,应降低lambda的值。
初始化各lambda的值,使用数组测试各个lambda的代价情况。可以观察到lambda等于3左右时代价都达到最低点。
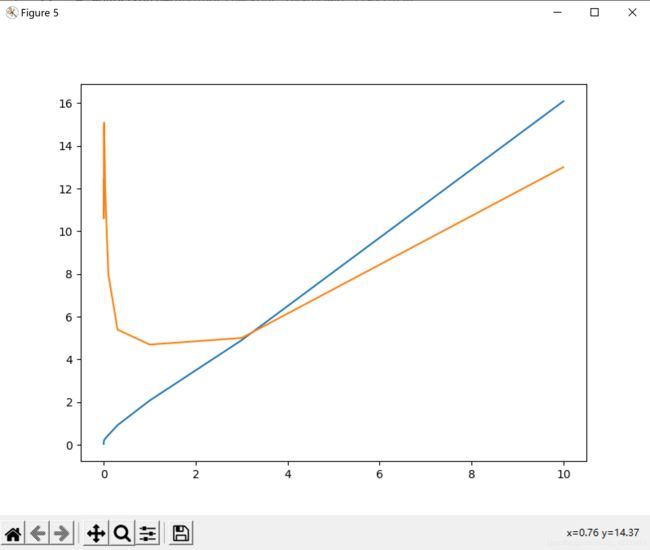
打印之前的数据与lambda不同时的代价,根据数据显示在测试集(test)上的结果得到lambda等于0.3时更优。