【理论+实践】史上最全-论文中常用的图像分割评价指标-附完整代码
图像分割的评价指标非常多,论文中常用的包括像素准确率(Pixel Accuracy, PA)、交并比(Intersection-Over-Union,IOU)、Dice系数(Dice Coeffcient), 豪斯多夫距离( Hausdorff distance,HD95),体积相关误差(relative volume error, RVE)。
文末还为懒癌星人提供一站式服务,只需修改地址,就可以实现所有指标,并且将结果存为Excel。
接下来,一一为大家解答。内容超多,建议收藏,需要用到时再来学习。
文中所有案例均是二分类,label中只有0和1
文章目录
- 1 像素准确率
-
- 1.1 理论
- 1.2 代码中如何表达
- 2 交并比 IoU
-
- 2.1 理论
- 2.2. 代码中如何表达
- 3 骰子系数Dice
-
- 3.1 原理
- 3.2 代码中如何实现
- 4 表面距离计算
-
- 4.1 Hausdorff distance 豪斯多夫距离
- 4.2 代码如何实现 H D 95 HD_{95} HD95和ASD
- 5 相关体积误差 RVE
- 6 为懒癌星人进行打包服务
1 像素准确率
1.1 理论
定义: 它是图像中正确分类的像素百分比。即分类正确的像素占总像素的比例。用公式可表示为:
P A = ∑ i = 0 n p i i ∑ i = 0 n ∑ j = 0 n p i j = T P + T N T P + T N + F P + F N PA =\frac{\sum_{i=0}^{n} p_{ii}}{\sum_{i=0}^{n} \sum_{j=0}^{n}p_{ij}} = \frac{TP + TN}{TP +TN + FP + FN} PA=∑i=0n∑j=0npij∑i=0npii=TP+TN+FP+FNTP+TN
其中:
- n : 类别总数,包括背景的话就是n+1
- p i i p_{ii} pii: 真实像素类别为 i i i 的像素被预测为类别 i i i 的总数量,就是对于真实类别为 i i i 的像素来说,分对的像素总数有多少。
- p i j p_{ij} pij: 真实像素类别为 i i i 的像素被预测为类别 j j j 的总数量, 换句话说,就是对于类别为 i i i 的像素来说,被错分成类别 j j j 的数量有多少。
- TP: 真阳性数,在label中为阳性,在预测值中也为阳性的个数
- TN: 真阴性数, 在label中为阴性,在预测值中也为阴性的个数
- FP: 假阳性数, 在label中为阴性,在预测值中为阳性的个数
- FN: 假阴性数, 在label中为阳性,在预测值中为阴性的个数
TP+TN+FP+FN=总像素数
TP+TN=正确分类的像素数
因此,PA 可以用两种方式来计算。
下面使用一个3 * 3 简单地例子来说明: 下图中TP=3,TN=4, FN=2, FP=0

P A = 3 + 4 3 + 4 + 2 = 77.8 % PA = \frac{3 + 4}{3+4+2}=77.8\% PA=3+4+23+4=77.8%
即图中正确分类的像素数为7,总像素数为9。
1.2 代码中如何表达
def binary_pa(s, g):
"""
calculate the pixel accuracy of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
pa = ((s == g).sum()) / g.size
return pa
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
pa = binary_pa(s, g)
是不是就很简单~~~~
思考一下,PA很简单,但是,它绝不是最好的指标。

在这个案例中,即使模型什么也没有分割出来,但他的PA = 95%, what???
嗯。我们的计算有问题吗?不。完全正确。只是背景类是原始图像的 95%。因此,如果模型将所有像素分类为该类,则 95% 的像素被准确分类,而其他 5% 则没有。
因此,尽管您的准确率高达 95%,但您的模型返回的是完全无用的预测。这是为了说明高像素精度并不总是意味着卓越的分割能力。
这个问题称为类别不平衡。当我们的类极度不平衡时,这意味着一个或一些类在图像中占主导地位,而其他一些类只占图像的一小部分。不幸的是,类不平衡在许多现实世界的数据集中普遍存在,因此不容忽视。
因此,这个指标基本没什么指导意义。
2 交并比 IoU
Intersection-Over-Union (IoU),也称为 Jaccard 指数,是语义分割中最常用的指标之一……这是有充分理由的。IoU 是一个非常简单的指标,非常有效。
2.1 理论
简单地说,IoU 是预测分割和标签之间的重叠区域除以预测分割和标签之间的联合区域(两者的交集/两者的并集),如图所示。该指标的范围为 0–1 (0–100%),其中 0 表示没有重叠,1 表示完全重叠分割。
对于二元分类而言,其计算公式为:
I o U = ∣ A ⋂ B ∣ ∣ A ⋃ B ∣ = T P T P + F P + F N IoU = \frac{|A \bigcap B|}{|A \bigcup B|} = \frac{TP}{TP + FP + FN} IoU=∣A⋃B∣∣A⋂B∣=TP+FP+FNTP
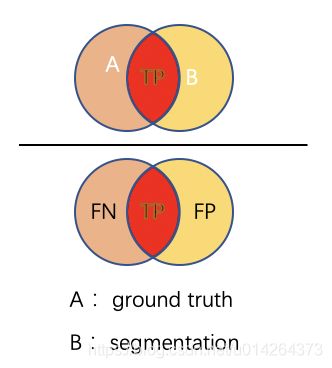
还是上面那个3 * 3 的例子,我们来计算一下它的IoU
I o U = 交 集 = 3 并 集 = 5 = T P = 3 T P + F P + F N = 5 = 60 % IoU=\frac{交集=3}{并集=5} = \frac{TP=3}{TP+FP+FN=5} = 60\% IoU=并集=5交集=3=TP+FP+FN=5TP=3=60%
2.2. 代码中如何表达
# IOU evaluation
def binary_iou(s, g):
assert (len(s.shape) == len(g.shape))
# 两者相乘值为1的部分为交集
intersecion = np.multiply(s, g)
# 两者相加,值大于0的部分为交集
union = np.asarray(s + g > 0, np.float32)
iou = intersecion.sum() / (union.sum() + 1e-10)
return iou
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
iou = binary_iou(s, g)
print(iou)
如果理解了原理,代码依然很简单。
tips: 分母中加了一项1e-10, 是为了防止分母为0的情况出错。
3 骰子系数Dice
3.1 原理
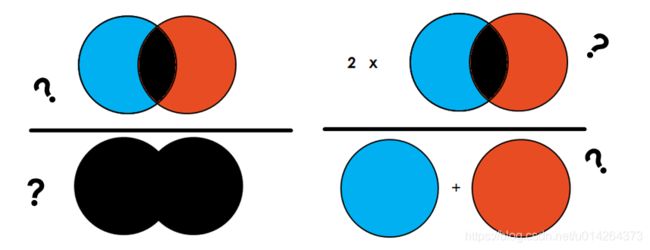
定义: Dice系数定义为两倍的交集除以像素和,也叫F1 score。Dice 系数与 IoU 非常相似,它们是正相关的。这意味着如果一个人说模型 A 在分割图像方面比模型 B 更好,那么另一个人也会这么说。
与 IoU 一样,它们的范围都从 0 到 1,其中 1 表示预测和真实之间的最大相似度。
其公式为:
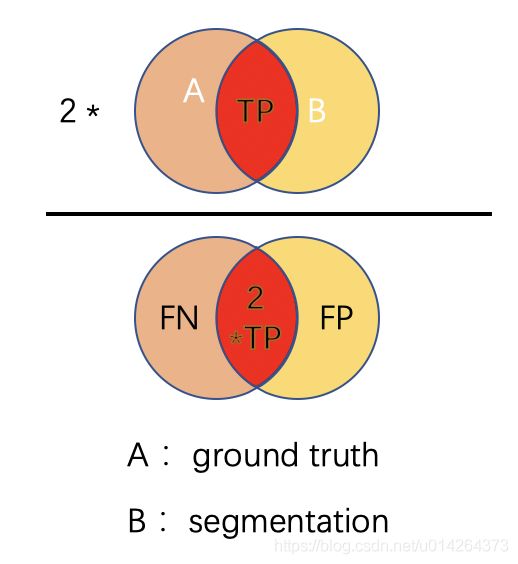
D i c e = 2 ∣ A ⋂ B ∣ ∣ A ∣ + ∣ B ∣ = 2 T P 2 T P + F P + F N Dice = \frac{2 |A \bigcap B|}{|A| + |B|} = \frac{2 TP}{2TP + FP + FN} Dice=∣A∣+∣B∣2∣A⋂B∣=2TP+FP+FN2TP
可以看到Dice系数对应于IoU,分子分母中的TP都取了两倍
还是上面那个3 * 3 的例子,我们来计算一下它的Dice:
D i c e = 2 ∗ 3 5 + 3 = 2 T P = 6 2 T P + F P + F N = 8 = 75 % Dice=\frac{2 * 3 }{5+ 3} = \frac{2TP=6}{2TP+FP+FN=8} = 75\% Dice=5+32∗3=2TP+FP+FN=82TP=6=75%
3.2 代码中如何实现
def binary_dice(s, g):
"""
calculate the Dice score of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
assert (len(s.shape) == len(g.shape))
prod = np.multiply(s, g)
s0 = prod.sum()
dice = (2.0 * s0 + 1e-10) / (s.sum() + g.sum() + 1e-10)
return dice
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
dice = binary_dice(s, g)
print(dice)
以上的指标意义可以重点掌握,以下有点难度,看不懂直接拉到最后,抄作业就好~~
4 表面距离计算
当我们评价图像分割的质量和模型表现时,经常会用到各类表面距离的计算。
比如
- Average surface distance 平均表面距离
- Hausdorff distance 豪斯多夫距离
- Surface overlap 表面重叠度
- Surface dice 表面dice值
- Volumetric dice 三维dice值
4.1 Hausdorff distance 豪斯多夫距离
将Hausdorff distance, HD 用于分割指标,主要是用来度量边界的分割准确度
HD 是描述两组点集之间相似程度的一种量度,它是两个点集之间距离的一种定义形式:假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的HD定义为:
H ( A , B ) = m a x ( h ( A , B ) , h ( B , A ) ) . . . . . . ( 1 ) H(A, B) = max(h(A, B), h(B,A)) ...... (1) H(A,B)=max(h(A,B),h(B,A))......(1)

- 式(1)称为双向Hausdorff distance,是Hausdorff distance的最基本形式;
- 式(2)中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离。即h(A,B)实际上首先对点集A中的每个点ai到距离此点ai最近的B集合中点bj之间的距离‖ai-bj‖进行排序,然后取该距离中的最大值作为h(A,B)的值;h(B,A)同理可得。
- 由式(1)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了两个点集间的最大不匹配程度。
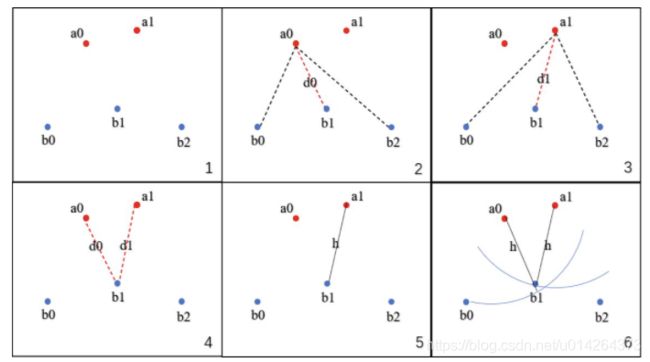
刚说了那么多,是不是也不是很清楚,只看公式确实是一件不好玩的事情,那我用网上常用的图来说明一下,还有一个比较简单清晰的计算流程。给定两个点集合A{ a0, a1, … }和B{ b0, b1, b2, …}
- 取A集合中的一点a0,计算a0到B集合中所有点的距离,保留最短的距离d0
- 遍历A集合中所有点,图中一共两点a0和a1,计算出d0和d1
- 比较所有的距离{ d0, d1 },选出最长的距离d1
- 这个最长的距离就是h,它是A→B的单向豪斯多夫距离,记为h( A, B
- 对于A集合中任意一点a,我们可以确定,以点a为圆心,h为半径的圆内部必有B集合中的
- 交换A集合和B集合的角色,计算B→A的单向豪斯多夫距离h( B, A ),选出h( A, B )和h( B, A )中最长的距离,就是A,B集合的双向豪斯多夫距离
此部分参考链接
在实际计算中,我们并不是选取的不是最大距离,而是将距离从大到小排列后,取排名为5%的距离。这么做的目的是为了排除一些离群点所造成的不合理的距离,保持整体数值的稳定性。所以也叫== H D 95 HD_{95} HD95.==
4.2 代码如何实现 H D 95 HD_{95} HD95和ASD
# Hausdorff and ASSD evaluation
def get_edge_points(img):
"""
get edge points of a binary segmentation result
"""
dim = len(img.shape)
if (dim == 2):
strt = ndimage.generate_binary_structure(2, 1)
else:
strt = ndimage.generate_binary_structure(3, 1) # 三维结构元素,与中心点相距1个像素点的都是邻域
ero = ndimage.morphology.binary_erosion(img, strt)
edge = np.asarray(img, np.uint8) - np.asarray(ero, np.uint8)
return edge
def binary_hausdorff95(s, g, spacing=None):
"""
get the hausdorff distance between a binary segmentation and the ground truth
inputs:
s: a 3D or 2D binary image for segmentation
g: a 2D or 2D binary image for ground truth
spacing: a list for image spacing, length should be 3 or 2
"""
s_edge = get_edge_points(s)
g_edge = get_edge_points(g)
image_dim = len(s.shape)
assert (image_dim == len(g.shape))
if (spacing == None):
spacing = [1.0] * image_dim
else:
assert (image_dim == len(spacing))
img = np.zeros_like(s)
if (image_dim == 2):
s_dis = GeodisTK.geodesic2d_raster_scan(img, s_edge, 0.0, 2)
g_dis = GeodisTK.geodesic2d_raster_scan(img, g_edge, 0.0, 2)
elif (image_dim == 3):
s_dis = GeodisTK.geodesic3d_raster_scan(img, s_edge, spacing, 0.0, 2)
g_dis = GeodisTK.geodesic3d_raster_scan(img, g_edge, spacing, 0.0, 2)
dist_list1 = s_dis[g_edge > 0]
dist_list1 = sorted(dist_list1)
dist1 = dist_list1[int(len(dist_list1) * 0.95)]
dist_list2 = g_dis[s_edge > 0]
dist_list2 = sorted(dist_list2)
dist2 = dist_list2[int(len(dist_list2) * 0.95)]
return max(dist1, dist2)
# 平均表面距离
def binary_assd(s, g, spacing=None):
"""
get the average symetric surface distance between a binary segmentation and the ground truth
inputs:
s: a 3D or 2D binary image for segmentation
g: a 2D or 2D binary image for ground truth
spacing: a list for image spacing, length should be 3 or 2
"""
s_edge = get_edge_points(s)
g_edge = get_edge_points(g)
image_dim = len(s.shape)
assert (image_dim == len(g.shape))
if (spacing == None):
spacing = [1.0] * image_dim
else:
assert (image_dim == len(spacing))
img = np.zeros_like(s)
if (image_dim == 2):
s_dis = GeodisTK.geodesic2d_raster_scan(img, s_edge, 0.0, 2)
g_dis = GeodisTK.geodesic2d_raster_scan(img, g_edge, 0.0, 2)
elif (image_dim == 3):
s_dis = GeodisTK.geodesic3d_raster_scan(img, s_edge, spacing, 0.0, 2)
g_dis = GeodisTK.geodesic3d_raster_scan(img, g_edge, spacing, 0.0, 2)
ns = s_edge.sum()
ng = g_edge.sum()
s_dis_g_edge = s_dis * g_edge
g_dis_s_edge = g_dis * s_edge
assd = (s_dis_g_edge.sum() + g_dis_s_edge.sum()) / (ns + ng)
return assd
这部分的计算相对有难度,另外,对于表面距离的计算还有公开库可用,如表面距离计算库, 可以实现上述距离算法。
5 相关体积误差 RVE
relative volume error, RVE, 暂时没找到很好的解释,可以参考:rve参考链接
公式为:
R V E ( R a , R b ) = a b s ( ∣ R a ∣ − ∣ R b ∣ ) ∣ R b ∣ RVE(R_a, R_b) = \frac{abs(|R_a|-|R_b|)}{|R_b|} RVE(Ra,Rb)=∣Rb∣abs(∣Ra∣−∣Rb∣)
- R_a: segmentation results
- R_b: ground truth
在代码中的实现为:
def binary_relative_volume_error(s_volume, g_volume):
s_v = float(s_volume.sum())
g_v = float(g_volume.sum())
assert (g_v > 0)
rve = abs(s_v - g_v) / g_v
return rve
6 为懒癌星人进行打包服务
是不是想一键get同款,复制下面代码,只需改名字就可以拿到所有的指标结果。适用于三维数据,数据格式为nii.gz…如果是二维数据,需要给一下数据读取方式。
# 计算三维下各种指标
from __future__ import absolute_import, print_function
import pandas as pd
import GeodisTK
import numpy as np
from scipy import ndimage
# pixel accuracy
def binary_pa(s, g):
"""
calculate the pixel accuracy of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
pa = ((s == g).sum()) / g.size
return pa
# Dice evaluation
def binary_dice(s, g):
"""
calculate the Dice score of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
assert (len(s.shape) == len(g.shape))
prod = np.multiply(s, g)
s0 = prod.sum()
dice = (2.0 * s0 + 1e-10) / (s.sum() + g.sum() + 1e-10)
return dice
# IOU evaluation
def binary_iou(s, g):
assert (len(s.shape) == len(g.shape))
# 两者相乘值为1的部分为交集
intersecion = np.multiply(s, g)
# 两者相加,值大于0的部分为交集
union = np.asarray(s + g > 0, np.float32)
iou = intersecion.sum() / (union.sum() + 1e-10)
return iou
# Hausdorff and ASSD evaluation
def get_edge_points(img):
"""
get edge points of a binary segmentation result
"""
dim = len(img.shape)
if (dim == 2):
strt = ndimage.generate_binary_structure(2, 1)
else:
strt = ndimage.generate_binary_structure(3, 1) # 三维结构元素,与中心点相距1个像素点的都是邻域
ero = ndimage.morphology.binary_erosion(img, strt)
edge = np.asarray(img, np.uint8) - np.asarray(ero, np.uint8)
return edge
def binary_hausdorff95(s, g, spacing=None):
"""
get the hausdorff distance between a binary segmentation and the ground truth
inputs:
s: a 3D or 2D binary image for segmentation
g: a 2D or 2D binary image for ground truth
spacing: a list for image spacing, length should be 3 or 2
"""
s_edge = get_edge_points(s)
g_edge = get_edge_points(g)
image_dim = len(s.shape)
assert (image_dim == len(g.shape))
if (spacing == None):
spacing = [1.0] * image_dim
else:
assert (image_dim == len(spacing))
img = np.zeros_like(s)
if (image_dim == 2):
s_dis = GeodisTK.geodesic2d_raster_scan(img, s_edge, 0.0, 2)
g_dis = GeodisTK.geodesic2d_raster_scan(img, g_edge, 0.0, 2)
elif (image_dim == 3):
s_dis = GeodisTK.geodesic3d_raster_scan(img, s_edge, spacing, 0.0, 2)
g_dis = GeodisTK.geodesic3d_raster_scan(img, g_edge, spacing, 0.0, 2)
dist_list1 = s_dis[g_edge > 0]
dist_list1 = sorted(dist_list1)
dist1 = dist_list1[int(len(dist_list1) * 0.95)]
dist_list2 = g_dis[s_edge > 0]
dist_list2 = sorted(dist_list2)
dist2 = dist_list2[int(len(dist_list2) * 0.95)]
return max(dist1, dist2)
# 平均表面距离
def binary_assd(s, g, spacing=None):
"""
get the average symetric surface distance between a binary segmentation and the ground truth
inputs:
s: a 3D or 2D binary image for segmentation
g: a 2D or 2D binary image for ground truth
spacing: a list for image spacing, length should be 3 or 2
"""
s_edge = get_edge_points(s)
g_edge = get_edge_points(g)
image_dim = len(s.shape)
assert (image_dim == len(g.shape))
if (spacing == None):
spacing = [1.0] * image_dim
else:
assert (image_dim == len(spacing))
img = np.zeros_like(s)
if (image_dim == 2):
s_dis = GeodisTK.geodesic2d_raster_scan(img, s_edge, 0.0, 2)
g_dis = GeodisTK.geodesic2d_raster_scan(img, g_edge, 0.0, 2)
elif (image_dim == 3):
s_dis = GeodisTK.geodesic3d_raster_scan(img, s_edge, spacing, 0.0, 2)
g_dis = GeodisTK.geodesic3d_raster_scan(img, g_edge, spacing, 0.0, 2)
ns = s_edge.sum()
ng = g_edge.sum()
s_dis_g_edge = s_dis * g_edge
g_dis_s_edge = g_dis * s_edge
assd = (s_dis_g_edge.sum() + g_dis_s_edge.sum()) / (ns + ng)
return assd
# relative volume error evaluation
def binary_relative_volume_error(s_volume, g_volume):
s_v = float(s_volume.sum())
g_v = float(g_volume.sum())
assert (g_v > 0)
rve = abs(s_v - g_v) / g_v
return rve
def compute_class_sens_spec(pred, label):
"""
Compute sensitivity and specificity for a particular example
for a given class for binary.
Args:
pred (np.array): binary arrary of predictions, shape is
(height, width, depth).
label (np.array): binary array of labels, shape is
(height, width, depth).
Returns:
sensitivity (float): precision for given class_num.
specificity (float): recall for given class_num
"""
tp = np.sum((pred == 1) & (label == 1))
tn = np.sum((pred == 0) & (label == 0))
fp = np.sum((pred == 1) & (label == 0))
fn = np.sum((pred == 0) & (label == 1))
sensitivity = tp / (tp + fn)
specificity = tn / (tn + fp)
return sensitivity, specificity
def get_evaluation_score(s_volume, g_volume, spacing, metric):
if (len(s_volume.shape) == 4):
assert (s_volume.shape[0] == 1 and g_volume.shape[0] == 1)
s_volume = np.reshape(s_volume, s_volume.shape[1:])
g_volume = np.reshape(g_volume, g_volume.shape[1:])
if (s_volume.shape[0] == 1):
s_volume = np.reshape(s_volume, s_volume.shape[1:])
g_volume = np.reshape(g_volume, g_volume.shape[1:])
metric_lower = metric.lower()
if (metric_lower == "dice"):
score = binary_dice(s_volume, g_volume)
elif (metric_lower == "iou"):
score = binary_iou(s_volume, g_volume)
elif (metric_lower == 'assd'):
score = binary_assd(s_volume, g_volume, spacing)
elif (metric_lower == "hausdorff95"):
score = binary_hausdorff95(s_volume, g_volume, spacing)
elif (metric_lower == "rve"):
score = binary_relative_volume_error(s_volume, g_volume)
elif (metric_lower == "volume"):
voxel_size = 1.0
for dim in range(len(spacing)):
voxel_size = voxel_size * spacing[dim]
score = g_volume.sum() * voxel_size
else:
raise ValueError("unsupported evaluation metric: {0:}".format(metric))
return score
if __name__ == '__main__':
import os
import nibabel as nib
seg_path = '你的分割结果文件夹'
gd_path = '你的label文件夹'
save_dir = 'excel 存放文件夹'
seg = sorted(os.listdir(seg_path))
dices = []
hds = []
rves = []
case_name = []
senss = []
specs = []
for name in seg:
if not name.startswith('.') and name.endswith('nii.gz'):
# 加载label and segmentation image
seg_ = nib.load(os.path.join(seg_path, name))
seg_arr = seg_.get_fdata().astype('float32')
gd_ = nib.load(os.path.join(gd_path, name))
gd_arr = gd_.get_fdata().astype('float32')
case_name.append(name)
# 求hausdorff95距离
hd_score = get_evaluation_score(seg_arr, gd_arr, spacing=None, metric='hausdorff95')
hds.append(hd_score)
# 求体积相关误差
rve = get_evaluation_score(seg_arr, gd_arr, spacing=None, metric='rve')
rves.append(rve)
# 求dice
dice = get_evaluation_score(seg_.get_fdata(), gd_.get_fdata(), spacing=None, metric='dice')
dices.append(dice)
# 敏感度,特异性
sens, spec = compute_class_sens_spec(seg_.get_fdata(), gd_.get_fdata())
senss.append(sens)
specs.append(spec)
# 存入pandas
data = {'dice': dices, 'RVE': rves, 'Sens': senss, 'Spec': specs, 'HD95': hds}
df = pd.DataFrame(data=data, columns=['dice', 'RVE', 'Sens', 'Spec', 'HD95'], index=case_name)
df.to_csv(os.path.join(save_dir, 'metrics.csv'))
文章持续更新,可以关注微信公众号【医学图像人工智能实战营】获取最新动态,一个关注于医学图像处理领域前沿科技的公众号。坚持已实践为主,手把手带你做项目,打比赛,写论文。凡原创文章皆提供理论讲解,实验代码,实验数据。只有实践才能成长的更快,关注我们,一起学习进步~
我是Tina, 我们下篇博客见~
最后,求点赞,评论,收藏。或者一键三连
![]()