【人工智能 学习总结】第三章 搜索策略（1）

3.1搜索的基本概念

3.1.1搜索的含义

（1）概念

搜索就是要寻找一个操作序列，使问题从初始状态转换到目标状态。这个操作序列就是目标的解。换言之，就是根据问题的实际情况，按照一定的策略或规则，从知识库中寻找可利用的知识，从而构造一条使问题获得解决的推理路线的过程

（2）类型

①按是否使用启发式信息：盲目搜索、启发式搜索；

②按问题的表示方式：状态空间搜索、与或树搜索

3.1.2状态空间法

（1）概念

基于解空间的问题表示和求解方法就是状态空间法。状态空间搜索的研究焦点在于设计高效的搜索算法，以降低搜索代价并解决组合爆炸问题

（2）状态空间及其搜索的表示

①状态

是表示问题求解过程中每一步问题状况的数据结构，它可形式地表示为：

 ={ 0, 1, …}

当对每一个分量都给以确定的值时，就得到了一个具体的状态

②操作（算符）

是把问题从一种状态变换为另一种状态的手段。操作可以是一个机械步骤，一个运算，一条规则或一个过程。操作可理解为状态集合上的一个函数，它描述了状态之间的关系

③状态空间

用来描述一个问题的全部状态以及这些状态之间的相互关系

常用一个三元组表示为：(S, F, G)

其中，S为问题的所有初始状态的集合；F为操作的集合；G为目标状态的集合

例：

 

 

3.1.3问题归约法

（1）概念

是另一种对问题进行描述及求解的办法。其基本思想是：对问题进行分解和变换，将此问题最终变为一个子问题的集合，通过求解子问题达到求解原问题的目的

由下面3个部分组成：

①一个初始问题的描述

②一套把问题变成子问题的操作符

③一套本原问题的描述

（2）与或树的相关概念

①节点与弧线

父节点：是一个初始问题或是可分解为子问题的问题节点

子节点：是一个初始问题或是子问题分解的子问题节点

或节点：只要解决某个问题就可解决其父问题的节点集合

与节点：只有解决所有子问题，才能解决其父问题的节点集合

端节点：没有子节点的节点

终止节点：本原问题所对应的节点。由此可见，终止节点一定是端节点，而端节点却不一定是终止节点

弧线：是父辈节点指向子节点的圆弧连线

②或树、与树、与/或树和解树

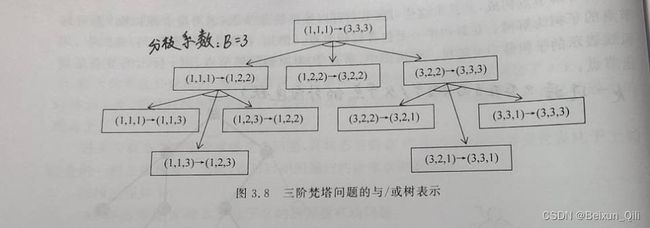
（3）例：

 

3.2状态空间搜索

3.2.1盲目搜索

（1）算法的数据结构和符号约定

①Open表：用于存放刚生成的节点，表结构如下所示

节点	父节点编号

②Closed表：用于存放已经扩展或将要扩展的节点，表结构如下所示

编号	节点	父节点编号

S0：表示问题的初始状态

G：表示搜索过程所得到的搜索图

M：表示当前扩展节点新生成的且不为自己先辈的子节点集

（2）一般图搜索

是在状态空间中搜索从初始状态到目标状态解答路径的过程

其中，状态空间搜索的基本思想可以概括为：

将问题的初始状态作为当前扩展节点对其进行扩展，生成一组子节点，然后检查问题的目标状态是否出现在这些子节点中

若出现，则搜索成功，找到了问题的解；若没出现，则再按照某种搜索策略从已生成的子节点中选择一个节点作为当前扩展节点

重复上述过程，直到目标状态出现在子节点中或者没有可供操作的节点为止。所谓对一个节点进行“扩展”是指对该节点用某个可用操作进行作用，生成该节点的一组子节点

一般图搜索步骤如下：

①把初始节点S0放入OPEN表，并建立目前仅包含S0的图G

②检查OPEN表是否为空，若为空则问题无解，失败退出

③把OPEN表的第一个节点取出放入CLOSED表，并记该节点为节点n

④判断节点n是否为目标节点。若是则得到了问题的解，成功退出

⑤考查节点n，生成一组子节点。把其中不是节点n先辈的那部分子节点记作集合M，并把这些子节点作为节点n的子节点加入G中

⑥针对M中子节点的不同情况，分别作如下处理：

<1>对那些没有在G中出现过的M成员设置一个指向其父节点（即节点n）的指针，并把它放OPEN表

<2>对那些原来已在G中出现过，确定是否需要修改它指向父节点的指针

 <3>对于那些先前已在G中出现并且已经扩展了的M成员，确定是否需要修改其后继节点指向父节点的指针

⑦按某种策略对OPEN表中的节点进行排序

⑧转第②步

（3）广度优先搜索（宽度优先搜索）

是一种先生成的节点先扩展的简单策略。从初始节点S0开始逐层向下扩展，只有当同一层的节点全部被搜索完以后，才能进入下一层继续搜索

其基本思想是：从初始节点S0，开始逐层对节点进行扩展并考察它是否为目标节点，在第n层节点还没有全部扩展并考察之前，不对第n+1层节点进行扩展

其搜索过程如下：

①把初始节点S0放入Open表中

②若Open表为空，则问题无解，退出

③把Open表的第一个节点（记为n）取出放入Closed表

④考察节点n是否为目标节点。若是，则得到问题的解，成功退出

⑤若节点n不可扩展，则转第②步

⑥扩展节点n，将其子节点放入Open表的尾部，并为每一个子节点设置指向父节点的指针，然后转第②步

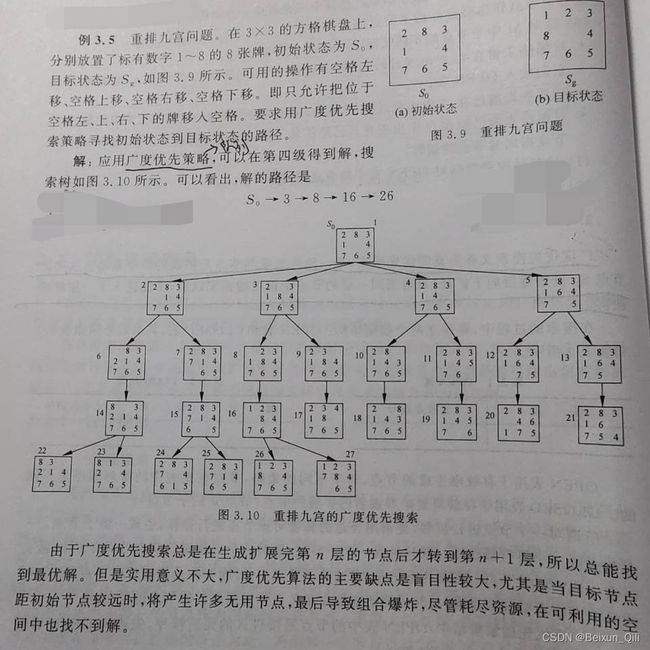
例：

（4）深度优先搜索

深度优先搜索总是先扩展后生成的节点

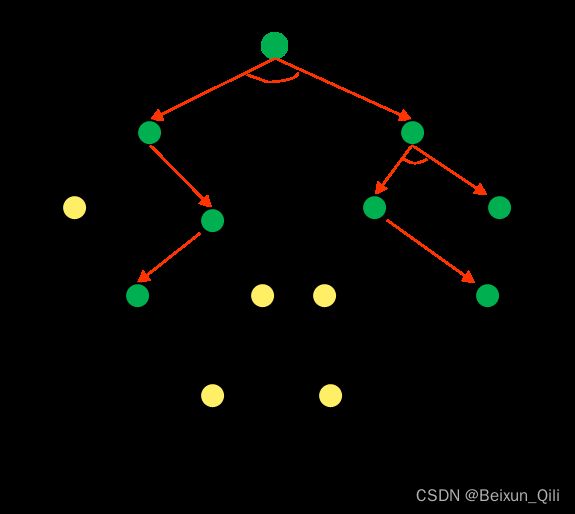
其基本思想是：从初始节点S0开始，在其子节点中选择一个最新生成的节点进行考察，如果该子节点不是目标节点且可以扩展，则扩展该子节点，然后再在此子节点的子节点中选择一个最新生成的节点进行考察，依此向下搜索，当到达某个子节点，此子节点既不是目标节点又不能继续扩展时，才选择其兄弟节点进行考察

其搜索过程如下：

①把初始节点S0放入Open表中

②若Open表为空，则问题无解，退出

③把Open表的第一个节点（记为n）取出放入Closed表

④考察节点n是否为目标节点。若是，则得到问题的解，退出

⑤若节点n不可扩展，则转第②步；

⑥扩展节点n，将其子节点放入Open表的首部，并为每一个子节点设置 指向父节点的指针， 然后转第②步

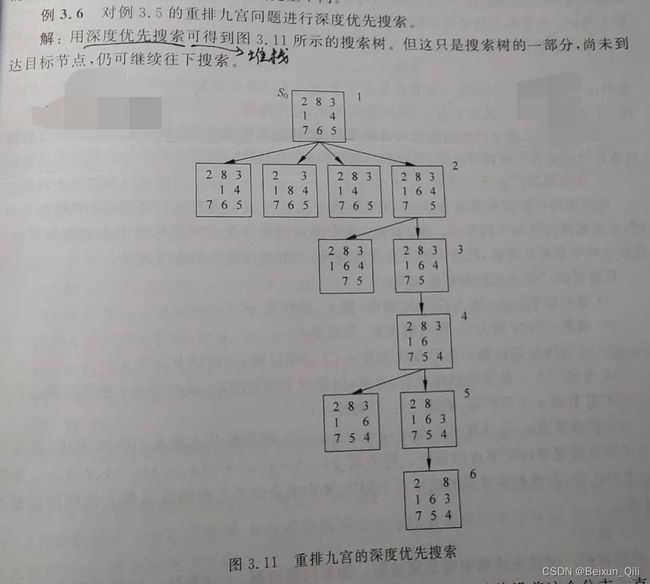
例：

 （5）代价树搜索

①代价树的代价表示

g(n 2) = g(n 1) + c(n 1, n 2)

其中，n 1与n 2分别表示某一父节点与其子节点，g(n)表示从初始节点S 0到节点n的代价，用c(n 1, n 2)表示从父节    点n 1到其子节点n 2的代价

②代价树的广度优先搜索

算法如下：

① 把初始节点S0放入Open表中，置S0的代价g(S 0)=0

②如果Open表为空，则问题无解 ，失败退出

③把Open表的第一个节点取出放入Closed表，并记该节点为n

④考察节点n是否为目标。若是，则找到了问题的解，成功退出，否则继续

⑤若节点n不可扩展，则转第②步,否则转第⑥步

⑥扩展节点n，生成其子节点n i (i=1, 2, …)，将这些子节点放入Open表中，并为每一个子节点设置指向父节点的指针

按如下公式 g(n i)=g(n)+c(n，n i)   (i=1,2,…)计算各子结点的代价，并根据各子结点的代价对Open表中的全部结点按由小到大的顺序排序

⑦转第②步

代价树的广度优先搜索策略时完备的

如果问题有解，上述算法一定能找到它，并且找到的一定是最优解

3.2.2状态空间的启发式搜索

（1）估价函数与启发式信息

①估价函数

估价函数f(n)被定义为从初始节点S0出发，约束经过节点n到达目标节点S g的所有路径中最小路径代价的估计值

它的一般形式为：f(n)=g(n)+h(n)

其中，g(n)是从初始节点S0到节点n的实际代价；h(n)是从节点n到目标节点S g的最优路径的估计代价

（2）启发信息

①有效地帮助确定扩展节点的信息

②有效的帮助决定哪些后继节点应被生成的信息

③能决定在扩展一个节点时哪些节点应从搜索树上删除的信息

（3）A算法（启发式搜索算法）

①把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)

②如果Open表为空，则问题无解 ，失败退出

③把Open表的第一个节点取出放入Closed表，并记该节点为n； 

④考察节点n是否为目标节点。若是，则找到了问题的解，成功退出

⑤若节点n不可扩展，则转第②步

⑥扩展节点n，生成其子节点n i (i=1, 2, …)，计算每一个子节点的估价值 f(n i)(i=1, 2, …)，并为每一个子节点设置指向父节点的指针，然后将这些子节点放入Open表中

⑦根据各节点的估价函数值，对Open表中的全部节点按从小到大的顺序重新进行排序

⑧转第②步

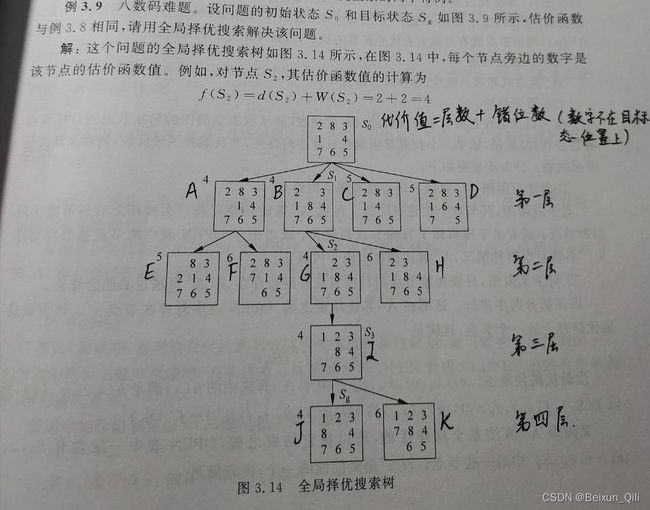
例：

 （4）A*算法

A*算法对A算法（全局择优的启发式搜索算法）中的g(n)和h(n)分别提出如下限制：

①g(n)是对最小代价g∗(n)的估计，且 g(n) ≥ g∗(n) 

②h(n)是最小代价h∗(n)的下界，即对任意节点n均有h(n) ≤ h∗(n)

即满足上述两条限制的A算法称为A*算法

（5）A*算法性质

①可采纳性；②单调性；③信息性

例：