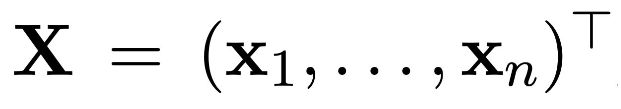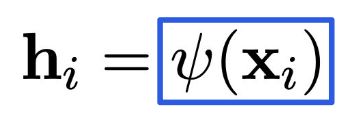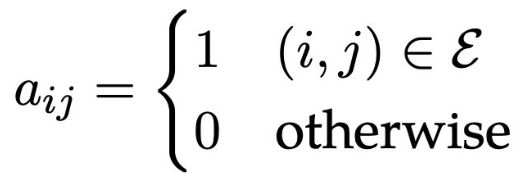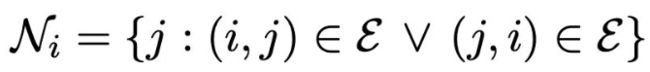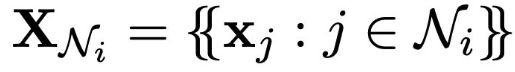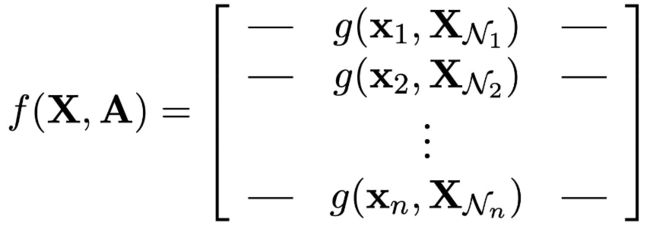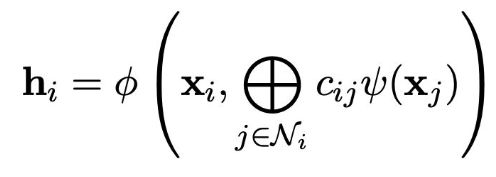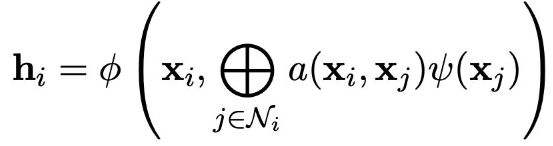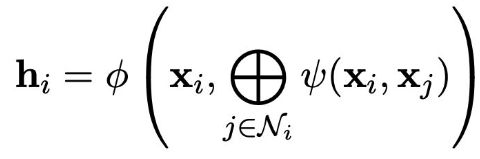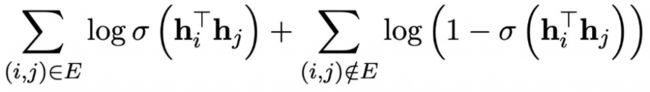图神经网络基础学习
注:本篇博客公式格式没有经过认真编辑,欢迎去我的博客:http://www.pinkman.tech/index.php/tech/2021/gnn-basic/ 或者知乎:https://zhuanlan.zhihu.com/p/356872702 获得更好的阅读体验。
本篇文章旨在通过最直白的语言解释一些GNN中的基础知识,涉及到的内容包括:
- GNN在现实中的应用
- 研究图问题的两个重要原则
- GNN是如何学习的
- GNN中信息如何传递?什么是卷积GNN,注意力GNN和信息传递GNN?
- 关于GNN的一些观点
本篇文章参考于Petar Veličković的教程,讲义位于:petar-v.com/talks/GNN-W。由于我刚接触这个领域,所以在书写过程中难免出错,欢迎在评论中指出。
一、现实世界中GNN的应用
判断分子特性
生物分子就是一个图结构,其中每一个原子是一个节点,连接原子的化学键就是一个边。关于分子有一些比较有趣的研究任务,比如判断一个分子是不是一种强烈的药物。此时,可以将该分子通过GNN来进行二分类。
GNN应用于化学领域这样训练以后,有一个好处是可以通过图神经网络发现各种各样的分子特性:将一个很大的候选分子库送入网络进行预测,可以选择GNN模型输出的候选100个分子集合,再进行化学测试。在这个领域还是非常有用的。
交通地图也是图结构
其中,每个十字路口可以是一个节点,每个道路就是一个边。
GNN应用在交通地图通过在交通地图上构建的GNN,可以用来回归预计抵达的时间(time to arrival, ETA)。
二、从CNN中观察
CNN的思想
第一个思想:只要图中出现某个信息,无论这个信息出现在哪里,都是有用的。比如检测某个物体,无论在图像中的哪里被检测到,只要被检测到就是成功的。所以才可以对整张图像进行扫描。这个思想叫做translational invariance。
第二个思想:离得近的图像像素之间的影响,远比离得远的像素的影响要大,因此才能够使用一个提取局部信息的卷积核。
我们接下来同样会利用这些思想,应用在图上。
图的特性
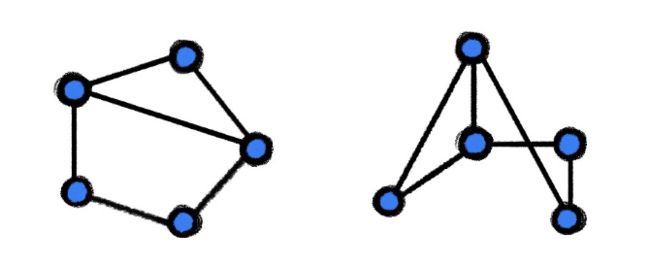
由于在图中不会指定任何的节点顺序,所以下面其实是一模一样的两幅图。我们需要图神经网络对这个输入,能够输出同样的信息。
两个相同的图三、排列不变性和排列相等性
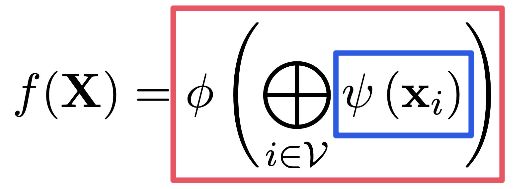
我们暂时先假设图中没有边,此时图是一个节点的集合。令(\boldsymbol{x}_i \in R^k) 表示节点 i 的 k 维特征。可以将所有的节点特征堆叠到一起,形成一个(n\times k)的特征矩阵。需要注意的是,在这里为节点指定了顺序,但是想要图的输出不会依赖于这个顺序。
为了研究组合方式的操作,定义如下的 (n\times n) 矩阵叫做排列矩阵。其中,每一行和每一列都只有一个1,其余都为0。这个矩阵的作用就是当左乘上述特征矩阵时,就将上述特征矩阵换了一个排列组合的方式。这个排列矩阵对于研究排列组合来说非常有用。
排列不变性 Permutation Invariance
我们的目标是:定义一个不依赖于输入节点顺序的函数(f(\boldsymbol{X})) 。
数学定义:如果 (f(\boldsymbol{X})) 是排列不变的,那么对于所有的排列矩阵P ,都有:(f(\boldsymbol{PX}) = f(\boldsymbol{X}) ) 。
排列相等性 Permutation Equivariance
但是,如果想要获得某一个节点的特征呢?此时就需要排列相等性了。它研究的是一个节点层面的排列性质。目标是找到不会改变节点顺序的函数。也就是说,如果我们改变节点的顺序,无论我们经过函数前改变,还是经过函数后改变,结果应该是一致的。
数学定义:如果 (f(\boldsymbol{X})) 是排列相等的,那么对于所有的排列矩阵P,都有:(f(\boldsymbol{PX}) = \boldsymbol{P}f(\boldsymbol{X}) ) 。
集合研究的基础
说到这里,大家也可以发现,排列相等性要求我们不能进行每个节点的特征交互,即特征矩阵的行与行之间的交互,所以我们只能够对每一个节点进行一个特征的映射。
其中的(\psi)是一个映射函数,独立地作用于对每个节点。将所有的 (\boldsymbol{h}_i) 堆叠起来,就得到了(\boldsymbol{H} = f(\boldsymbol{X}))。
另一方面,为了保证排列不变性,我们需要在最后添加一个聚集函数,例如求和,平均值,最大值等。这样我们就得到了最终的输出。
说了这么多,思想其实很简单,就是先单独对每个节点提取特征,然后将所有的特征整合起来,整合的过程要保证顺序不会影响到最终结果。
四、图中的学习
好了,现在可以研究图中有边的情况了。我们定义邻接矩阵 A,其中
这里为了便于表示,先忽略边的特征,比如距离,花费成本等。
将图中的节点进行排列时,由于节点的顺序变化会同时影响到连接它的所有边,在邻接矩阵中表示,就是邻接矩阵的行和列都要受到影响。具体来说,假如节点经过了 (\boldsymbol{P}) 的排列组合转换,那么邻接矩阵就会变为 (\boldsymbol{PAP}^T) 。
此时,排列不变性和排列相等性就变成了这样的表示:
图中的局部性:邻居节点
在前文提到的节点集合部分中,我们通过每个节点独立地提取特征保证了排列相等性。然而在图中,我们有一个非常有用的信息:一个节点的邻居节点。对于一个节点 i 来说,和它距离为1的节点集合可以表示为:
此时,我们可以在这个邻居节点的集合上提取特征,表示为
将这个提取特征的过程表示为函数 (g(\boldsymbol{x}i, \boldsymbol{X}{N_i})) 。
图神经网络
此时,我们终于可以了解到图神经网络是什么样的了。将上述的函数g作用于每一个节点及其邻居节点,得到最终的特征,这就是一个图神经网络的基础形式。
为了确保排列相等性,我们需要保证这里的函数g不依赖于邻居节点的顺序信息,因此,g应该是排列不变的。
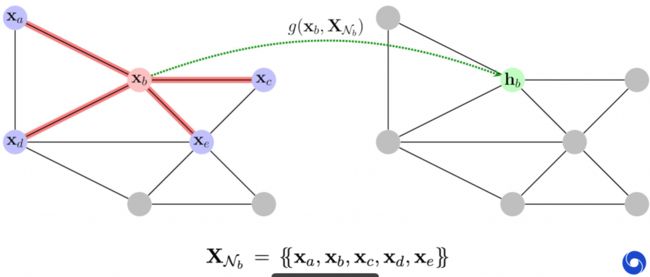
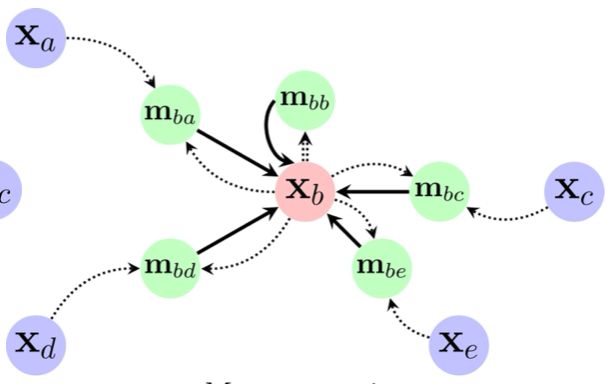
下图中是一个图神经网络提取特征的图示,通过输入一个节点b,及其周围的邻居节点给函数g,提取得到的隐向量,标记为 (\boldsymbol{h}_b)。
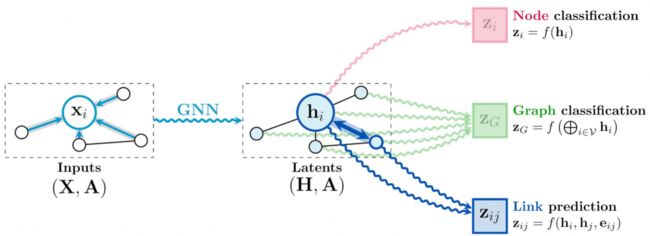
图神经网络提取特征图示得到了隐含向量以后,如何利用它们呢?这里给出几种常见的使用方式:
- 节点分类。得到某一个节点的的隐向量以后,利用该向量去对一个节点进行分类。
- 图分类。将所有节点的隐向量整合到一起,得到整个图的特征,然后利用这个特征去分类。比如上文提到的分子特性分类。
- 链接预测。输入两个节点的隐向量以及他们之间的边的信息,能够输出这两个节点之间相互作用的结果。这一点也非常有用,比如预测从一个节点到另一个节点的抵达时间。
以下图示表示了这一过程:
如何使用隐向量五、图中的信息传递
在GNN领域中,通常把前文中描述的 (f) 叫做GNN的一层, 叫做“扩散”、“传播”或者“信息传递”。如何定义函数 (g),是图神经网络中的重点,也是非常热门的研究领域。几乎所有提出的定义方式,可以按照空间偏好分为三类,分别是卷积(Convolutional),注意力(Attentional)和信息传递(Message-passing)。
卷积图神经网络
通过一个固定的权重 (c_{ij}) 来整合邻居节点的特征。通常来说,这里的权重通常直接依赖于节点之间边的信息(边的信息代表的是节点的相似度,比如两个节点距离越近,那么它们可能就越相似)。
卷积GNN示意图这种结构对于同质图来说很有用(同质图:图中的节点类型和关系类型都仅有一种),并且网络可以轻易扩展到很大的规模。
使用这类方法的经典模型包括:
- ChebyNet (Defferrard , NeurIPS’16) et al.
- GCN (Kipf & Welling, ICLR’17)
- SGC (Wu , ICML’19) et al.
注意力图卷积神经网络
注意力机制是近几年非常火的一个研究方向。应用在GNN中,就是将前文中固定的权重改为可学习的权重,以此来描述两个相邻节点之间的关系。用公式表示为:
注意力GNN示意图这种结构对于一些边中没有蕴含节点关系的图来说非常有效,适用于规模不是特别大的图,因为注意力机制会增加比较大的显存和计算量。
使用这类方法的经典模型包括:
- MoNet (Monti , CVPR’17) et al.
- GAT (Veličković , ICLR’18) et al.
- GaAN (Zhang , UAI’18) et al.
信息传递图神经网络
计算出一个向量(“信息”),通过边传递给其余节点。
用公式表示为:
信息传递GNN示意图其中 ,(m_{ij} = \psi)就是传递的信息。
因为有了信息的传递,这类模型可以拟合一些非常复杂的任务,但是可能会面临一些规模或者学习上的问题,因为需要计算和存储整个图中所有边计算出来的信息,而图中的边一般都比节点要多得多。
使用这类方法的经典模型包括:
- Interaction Networks (Battaglia ., NeurIPS’16) et al
- MPNN (Gilmer ., ICML’17) et al
- GraphNets (Battaglia ., 2018) et al
六、关于GNN的观点
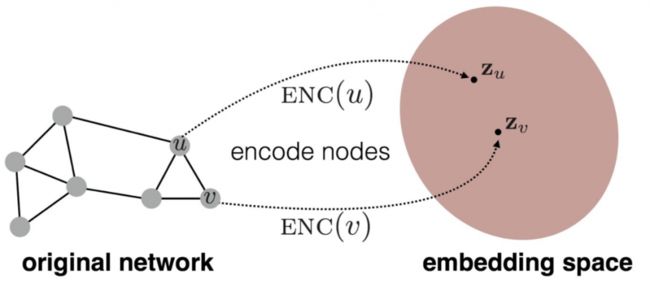
节点嵌入技术
这项技术的目的是,将图中的节点嵌入到隐空间中。
节点嵌入那么什么是一个好的嵌入表示呢?对于图来说,一个自然的想法就是,保留住图中的有用信息,而节点之间的有用信息,那就是边。所以就有了一个非常直接的目标:如果两个节点之间右边,那么他们在隐空间中应该是相近的,可以使用标准的二分类交叉熵损失函数来实现这个目标:
这个其实是一个更加广泛的方法簇——随机行走的一个特例。将上述损失函数中的 ,重新定义为 和 共同出现在一个随机行走的过程中。
这类方法在GNN面世前,是最主流的无监督图表示学习方法。有以下著名的算法:
- DeepWalk (Perozzi , KDD’14) et al.
- node2vec (Grover & Leskovec, KDD’16)
- LINE (Tang , WWW’15) et al.
值得注意的一点是,通过这种方法,能够学习到节点局部的相似性。因为在隐空间中距离比较近的节点,可能在原先的图结构中是存在边相连的,就是他们互相是邻居节点。这是随机行走方法的一个内在的特点。但是,这恰恰就是卷积GNN的设计思想:强迫邻居学习到相似的特征,这是因为两个图中相邻的节点,可能会有很多个共同的邻居节点,所以能够学习到相似的特征。关于此,有两个有用的推论:
- 随机行走的目标可能不能给GNN提供有用的信号
- 有时,DeepWalk能得到与未训练的卷积GNN相同的效果!(Veličković et al., ICLR’19)
与NLP的关系
节点嵌入技术,其实和NLP中的词向量技术如出一辙:
- 节点可以和词对应
- 随机行走和一个句子对应
- node2vec技术对应于word2vec技术
- 优化目标基本是一模一样的
并不单纯只有NLP可以嵌入到GNN的设计思想中,GNN其实也可以嵌入到NLP的设计思想中,两门技术是非常相通的。
在NLP领域中,一个句子中的不同单词,是会互相交互的,比如出现一个词,另外一个词的含义可能完全变了。我们可以使用图来表示这种交互,但是这个交互信息并不是直接提供的,此时,一个常见的假设就是去初始化一个完全图(完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连),然后让网络去学习相互之间的关系。而这,就是Transformers的思想!
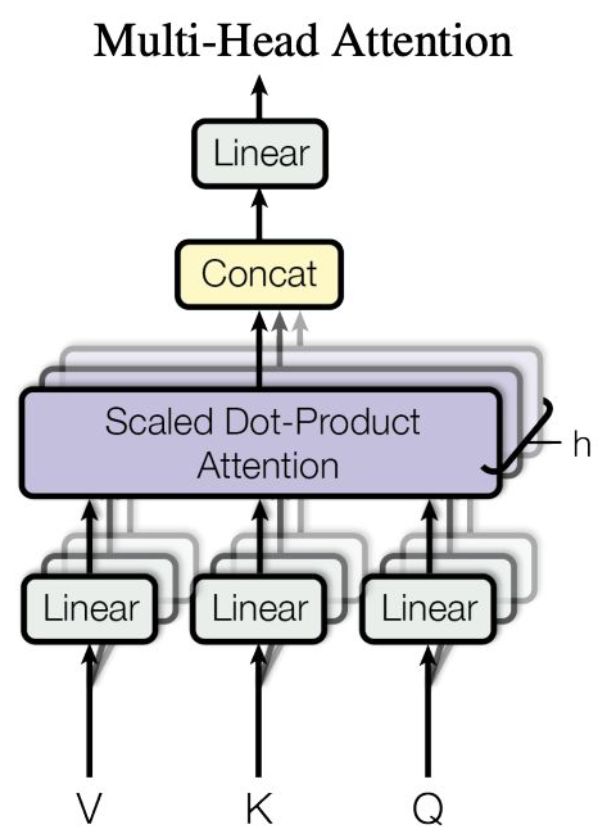
可以将Transformer视作GNN的一种,它是一个完全图,属于注意力图神经网络分类下。attention可以看做图中的一种软相邻。(Joshi (The Gradient; 2020).)
多头注意力机制感谢您的阅读,如果觉得这篇文章对您有帮助,欢迎分享收藏!最后附上教程的原始视频链接。