datawhale 6月学习——图神经网络：消息传递图神经网络

前情回顾

1. 图神经网络：图数据表示及应用

1 消息传递范式

消息传递范式是一种聚合邻接节点信息来更新中心节点信息的范式，它将卷积算子推广到了不规则数据领域，实现了图与神经网络的连接。
此范式包含三个步骤

1. 邻接节点信息变换
2. 邻接节点信息聚合到中心节点
3. 聚合信息变换

图相对于其他结构化数据，其节点间存在联系，但是节点和节点间的关系没有那么规则，因此需要专门的消息传递方式来实现节点间信息的相互传递。
这个消息传递方式的表述是：

用${\mathbf{x}}_i^{(k-1)}\in {\mathbb{R}}^F$表示$(k-1)$层中节点$i$的节点特征，${\mathbf{e}}_{j,i}\in {\mathbb{R}}^D$ 表示从节点$j$到节点$i$的边的特征，消息传递图神经网络可以描述为
$${\mathbf{x}}_i^{(k)}={\gamma }^{(k)}\left({\mathbf{x}}_i^{(k-1)},{\square }_{j\in \mathcal{N}(i)}{\varphi }^{(k)}\left({\mathbf{x}}_i^{(k-1)},{\mathbf{x}}_j^{(k-1)},{\mathbf{e}}_{j,i}\right)\right),$$
其中$\square$表示可微分的、具有排列不变性（函数输出结果与输入参数的排列无关）的函数。具有排列不变性的函数有，和函数、均值函数和最大值函数。$\gamma$和$\varphi$表示可微分的函数，如MLPs（多层感知器）。此处内容来源于CREATING MESSAGE PASSING NETWORKS。

2 PyG中的MessagePassing

2.1 MessagePassing简介

Pytorch Geometric(PyG)提供了MessagePassing基类，它实现了消息传播的自动处理，继承该基类可使我们方便地构造消息传递图神经网络，我们只需定义函数$\varphi$，即message()函数，和函数$\gamma$，即update()函数，以及使用的消息聚合方案，即aggr="add"、aggr="mean"或aggr="max"。
基于MessagePassing，我们可以实现诸多消息聚合方法。

2.2 基于MessagePassing实现GCNConv

2.2.1 GCNConv定义及实现代码

GCNConv的数学定义为
$${\mathbf{x}}_i^{(k)}=\sum _{j\in \mathcal{N}(i)\cup \{i\}}\frac{1}{\sqrt{\mathrm{deg}(i)}\cdot \sqrt{\mathrm{deg}(j)}}\cdot \left(\mathbf{\Theta }\cdot {\mathbf{x}}_j^{(k-1)}\right),$$
其中，相邻节点的特征首先通过权重矩阵$\mathbf{\Theta }$进行转换，然后按端点的度进行归一化处理，最后进行加总。这个公式可以分为以下几个步骤：

1. 向邻接矩阵添加自环边；
2. 实现节点特征矩阵的线性变换；
3. 对特征进行归一化；
4. 对邻居节点特征进行聚合操作；
5. 直接返回信息聚合的输出。

其源码如下：

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(GCNConv, self).__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm)

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j
    def update(self, aggr_out):
        # aggr_out has shape [N, out_channels]

        # Step 5: Return new node embeddings.
        return aggr_out

下面结合源码进行逐步理解，此部分参考了GNN Review，Torch geometric GCNConv 源码分析 。

2.2.2 代码分析

forward

forward方法是调用该类后默认执行的方法，因此，大部分的处理流程都在其中有所体现。

• 1、向邻接矩阵添加自环边

edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

• 2、实现线性变换

self.lin = torch.nn.Linear(in_channels, out_channels)
x = self.lin(x)

其中in_channels是节点特征的维度，out_channels是我们自己设定的降维维度。
这一步是实现该网络层中实现维度变化最主要的步骤。

• 3、特征归一化

row, col = edge_index
deg = degree(row, size[0], dtype=x_j.dtype)  # [N, ]
deg_inv_sqrt = deg.pow(-0.5)   # [N, ]
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

上述实现了，求取节点度，并进行归一化的操作。首先计算了row(target)的度。deg[0]表示编号为0的节点的度，因此deg的长度为N。而deg_inv_sqrt[row]返回了长度为E的度数组。norm最终保存了所有边的标准化系数。

message

• 4、对邻居节点特征进行聚合操作
  这一步由调用propagate，到了message 函数中

norm.view(-1, 1) * x_j

这里需要明确x_j的由来，GNN Review中给了比较清晰的讲解

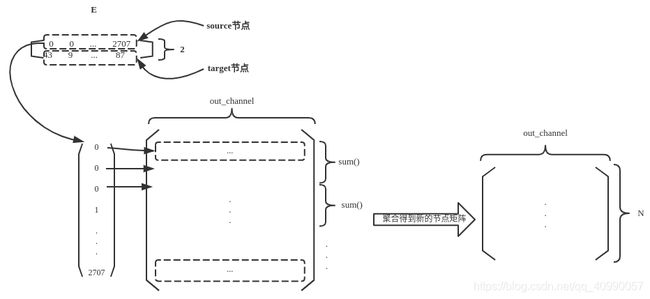
首先说明x_j的由来。这里E表示边的个数，
对边矩阵edge_index，形状为(2, E)，第一行表示边的source节点（在代码中是row，这两者在本文中等价），第二行表示边的target节点（在代码中是col，这两者在本文中等价），以target节点作为索引，从线性变换后的特征矩阵中索引得到target节点的特征矩阵，示意图如下

通过阅读源码可以发现，在具体的运行过程中，MessagePassing的内置方法，可以将输入的与x维度一致的矩阵变换为_i（源节点），_j（尾节点）的形式。而变换方式如上图所讲解的，是将节点信息根据edge_index中存储的连接关系，进行了变换，以方便信息的汇总计算。

update

• 5、直接返回聚合信息的输出
  这一部分主要通过update函数实现

def update(self, aggr_out):
    # aggr_out has shape [N, out_channels]

    # Step 5: Return new node embeddings.
    return aggr_out

2.3 MessagePassing的覆写及一层图神经网络的实现（作业）

2.3.1 作业任务及使用的数据集

作业具体任务如下

1. 请总结MessagePassing基类的运行流程。
2. 请复现一个一层的图神经网络的构造，总结通过继承MessagePassing基类来构造
   自己的图神经网络类的规范。

另一部分其实是前一版本的作业，需要实现以下任务

1. 请总结MessagePassing类的运行流程以及继承MessagePassing类的规范。
2. 请继承MessagePassing类来自定义以下的图神经网络类，并进行测试：
   1. 第一个类，覆写message函数，要求该函数接收消息传递源节点属性x、目标节点度d。
   2. 第二个类，在第一个类的基础上，再覆写aggregate函数，要求不能调用super类的aggregate函数，并且不能直接复制super类的aggregate函数内容。
   3. 第三个类，在第二个类的基础上，再覆写update函数，要求对节点信息做一层线性变换。
   4. 第四个类，在第三个类的基础上，再覆写message_and_aggregate函数，要求在这一个函数中实现前面message函数和aggregate函数的功能。

由于通过4个类的实现可以对MessagePassing的覆写有更好的认识，同时可以借助此构建一个自己的单层图神经网络，故结合两个版本的作业进行完成。
所有覆写的类均在以PyG内置的Planetoid数据集上进行测试，其详细介绍可见，torch_geometric.datasets.Planetoid
数据集调用如下：

from torch_geometric.datasets import Planetoid

dataset = Planetoid(root='/dataset/Cora', name='Cora')

data = dataset[0]

其维度属性如下

>>> data.x.shape
torch.Size([2708, 1433])
>>> data.edge_index.shape
torch.Size([2, 10556])

该数据集将在每一个网络层使用。

2.3.2 网络层的实现

网络层1：覆写message函数，要求该函数接收消息传递源节点属性x、目标节点度d

class Task1(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(Task1, self).__init__(aggr='add', flow='source_to_target')
        # "Add" aggregation (Step 5).
        # flow='source_to_target' 表示消息从源节点传播到目标节点
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        d = torch.tensor([deg[each] for each in col])

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm, d=d)

    def message(self, x_i, norm, d):
        # x_i has shape [E, out_channels]
        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_i * d.view(-1,1)

这部分任务的关键在于，需要理解x_i（源分量）及节点度计算维度。
在具体的数据集上实例化实现网络。

net = Task1(data.num_features,64) #降维到64
h_nodes = net(data.x,data.edge_index)

结果如下

>>> h_nodes
tensor([[ 0.2971,  0.1081, -0.0932,  ..., -0.2649, -0.0630, -0.1912],
        [ 0.3006, -0.2472,  0.2361,  ..., -0.7510,  0.1372,  0.6933],
        [-0.4272,  0.2311, -0.0678,  ..., -0.1067,  0.1662, -0.3736],
        ...,
        [-0.0975, -0.0159, -0.1837,  ..., -0.1785,  0.0262,  0.0722],
        [ 0.1165, -0.0020, -0.8961,  ..., -0.1192,  0.3227,  0.0175],
        [ 0.1090,  0.2917, -0.2882,  ..., -0.1695, -0.2707, -0.5407]],
       grad_fn=<ScatterAddBackward>)
>>> h_nodes.shape
torch.Size([2708, 64])

网络层2：在第一个类的基础上，再覆写aggregate函数，要求不能调用super类的aggregate函数，并且不能直接复制super类的aggregate函数内容

class Task2(Task1):
    def __init__(self, in_channels, out_channels):
        super(Task2, self).__init__(in_channels,out_channels)#aggr='add', flow='source_to_target')
        # "Add" aggregation (Step 5).
        # flow='source_to_target' 表示消息从源节点传播到目标节点
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def aggregate(self, inputs, index, ptr, dim_size):
        #print(scatter(inputs, index, dim=self.node_dim, dim_size=dim_size, reduce=self.aggr))
        result = torch.tensor([])
        for each in torch.arange(0,dim_size):
          re = inputs[index == each,:].sum(dim=self.node_dim,keepdims = True)
          result = torch.cat([result,re],dim = 0)
        return result

这部分主要是更改了aggregate函数，aggregate的super类里调用了scatter函数，此处不调用，只实现了加和的功能。
这部分任务有助于理解tensor的计算，需要注意维度的统一。
在具体的数据集上实例化实现网络。

net = Task2(data.num_features,64) #降维到64
h_nodes = net(data.x,data.edge_index)

结果如下

>>> h_nodes
tensor([[-0.1823, -0.2369,  0.0657,  ..., -0.3418,  0.1931, -0.1391],
        [-0.2718, -0.1814, -0.4894,  ..., -0.0500, -0.0139, -0.1708],
        [-0.4778, -0.4981,  0.3491,  ...,  0.1360, -0.0408, -0.2711],
        ...,
        [-0.1111, -0.0910, -0.1193,  ...,  0.0171,  0.2335,  0.1118],
        [-0.2256, -0.4605, -0.1228,  ..., -0.4107,  0.0388, -0.1020],
        [ 0.2963,  0.2233, -0.2384,  ..., -0.2396, -0.1495, -0.0926]],
       grad_fn=<CatBackward>)
>>> h_nodes.shape
torch.Size([2708, 64])

网络层3：在第二个类的基础上，再覆写update函数，要求对节点信息做一层线性变换

class Task3(Task2):
    def __init__(self, in_channels, out_channels):
        super(Task3, self).__init__(in_channels,out_channels)#(aggr='add', flow='source_to_target')
        # "Add" aggregation (Step 5).
        # flow='source_to_target' 表示消息从源节点传播到目标节点
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def update(self, input):
        lin = torch.nn.Linear(input.size(1), input.size(1))
        #print(input)
        return lin(input)

就是覆写了update函数，此部分有助于理解线性变换的实现，以及update的调用顺序。update于message及aggregate后调用。
在具体的数据集上实例化实现网络。

net = Task3(data.num_features,64) #降维到64
h_nodes = net(data.x,data.edge_index)

结果如下

>>> h_nodes
tensor([[-0.0444,  0.1647, -0.0913,  ..., -0.1520, -0.0345,  0.0860],
        [-0.2127,  0.0666,  0.0109,  ...,  0.1095, -0.0914,  0.1844],
        [-0.0642,  0.2746, -0.0437,  ..., -0.0793, -0.0684, -0.0082],
        ...,
        [-0.1104,  0.0154, -0.1064,  ...,  0.0940, -0.0353, -0.1686],
        [-0.3395,  0.2719,  0.0923,  ...,  0.0042, -0.1735, -0.1246],
        [-0.3156,  0.1010, -0.1129,  ...,  0.0511,  0.0072, -0.1393]],
       grad_fn=<AddmmBackward>)
>>> h_nodes.shape
torch.Size([2708, 64])

网络层4：在第三个类的基础上，再覆写message_and_aggregate函数，要求在这一个函数中实现前面message函数和aggregate函数的功能

from torch_sparse import SparseTensor 

class Task4(Task3):
    def __init__(self, in_channels, out_channels):
        super(Task3, self).__init__(in_channels,out_channels)#(aggr='add', flow='source_to_target')
        # "Add" aggregation (Step 5).
        # flow='source_to_target' 表示消息从源节点传播到目标节点
        self.lin = torch.nn.Linear(in_channels, out_channels)
    def forward(self, x, edge_index):
        # ....
        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)
        # Step 3: Compute normalization.
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        d = torch.tensor([deg[each] for each in col])

        adjmat = SparseTensor(row=edge_index[0], col=edge_index[1], value=torch.ones(edge_index.shape[1]))
        # 此处传的不再是edge_idex，而是SparseTensor类型的Adjancency Matrix
        return self.propagate(adjmat, x=x, norm=norm, d=d)
        
    def message_and_aggregate(self, edge_index, x_i, norm, d, dim_size, index):
        #print(index)
        #col = 
        inputs = norm.view(-1, 1) * x_i * d.view(-1,1)
        result = torch.tensor([])
        for each in torch.arange(0,dim_size):
            re = inputs[index == each,:].sum(dim=self.node_dim,keepdims = True)
            result = torch.cat([result,re],dim = 0)
        return result

这个任务有助于理解message和aggregate及message_and_aggregate间的相互替代关系，通过阅读MessagePassing的源码，我们可以发现，二者的相互替代是通过判断propagate函数的传入参数是否为SparseTensor实现的。

if (isinstance(edge_index, SparseTensor) and self.fuse and not self.__explain__):
    coll_dict = self.__collect__(self.__fused_user_args__, edge_index, size, kwargs)

    msg_aggr_kwargs = self.inspector.distribute(
                'message_and_aggregate', coll_dict)
            out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs)
...
elif isinstance(edge_index, Tensor) or not self.fuse:
...

因此，覆写关键在于，需要在调用propagate之前生成SparseTensor 对象，然后传入propagate
在具体的数据集上实例化实现网络。

net = Task4(data.num_features,64) #降维到64
h_nodes = net(data.x,data.edge_index)

结果如下

>>> h_nodes
tensor([[-0.1113, -0.0801, -0.2292,  ...,  0.0535,  0.1779, -0.1181],
        [ 0.0348, -0.0435, -0.1894,  ..., -0.0542,  0.0313, -0.1658],
        [ 0.2094,  0.1680, -0.4113,  ..., -0.1185,  0.4439,  0.3465],
        ...,
        [ 0.2054, -0.1037, -0.1079,  ..., -0.1217,  0.1056,  0.0740],
        [ 0.1576, -0.2716, -0.0894,  ...,  0.1226,  0.0324, -0.2275],
        [-0.1102,  0.1652, -0.2325,  ...,  0.0306, -0.0617, -0.0646]],
       grad_fn=<AddmmBackward>)
>>> h_nodes.shape
torch.Size([2708, 64])

2.3.3 小结MessagePassing基类的运行流程

通过上述案例，可以小结如下：

1. 默认调用forward方法
2. forward方法调用propagate方法实现前向传播
3. propagate为主要实现功能的函数，分为两种情况
   1. 传入对象为SparseTensor，则调用message_and_aggregate消息传递及聚合函数，然后调用update更新特征；
   2. 传入对象为Tensor，则依次调用message消息传递，aggregate聚合函数，然后调用update更新特征；

2.3.4 通过继承MessagePassing基类来构造自己图神经网络的规范

小结如下：

1. 可以通过改写forward，message_and_aggregate，message，aggregate，update等函数来构建自己的图神经网络。
2. forward是图神经网络类默认调用的方法，在forward中需要调用propagate。
3. propagate作为中间商，串起整个信息传递聚合及更新的核心流程，一般不需也不应覆写propagate，但要将需要的参数传入propagate。
4. 可以通过覆写message信息传递函数，改变需要传递的信息，需要理解_j，_i的含义（会默认计算），注意维度。
5. 可以通过覆写aggregate信息聚合函数，改变需要聚合的信息。
6. 可以通过覆写update信息更新函数，改变更新信息的方式。
7. 可以通过覆写message_and_aggregate函数，实现上述4及5点的功能，但需要注意，应生成SparseTensor对象传入propagate函数，来实现message_and_aggregate的运行。

在上述任务中，仍有许多基类参数未曾改变，如聚合方式aggr，信息传递方式flow等，有待进一步学习深入。

参考阅读

1. Datawhale组队学习
2. The “MessagePassing” Base Class
3. Torch geometric GCNConv 源码分析