KNN最近邻算法及其Python实现

转载：https://mp.weixin.qq.com/s?__biz=MzIzNDM2OTMzOQ==&mid=100000162&idx=1&sn=42ef091fc6974f3f57018c3dce8d8c9c#rd 

k-NN是一种基本的分类和回归方法，用于分类时，算法思路较简单：通过计算不同特征之间的距离方法来得到最近的k个训练实例，根据k个实例的类别采用多数表决等方式进行预测。而做回归分析时，则通过对k个实例取均值来做预测。因此我们可以看到k-NN的三个基本要素：k值选择、距离度量及分类决策规则。

一、算法分析

 

输入:训练集和类别的数据集表示为如下：

T={(x1,y1),(x2,y2),…,(xN,yN)}

其中，输出：实例x所属的类y。是实例的类别。

(1)    根据给定的距离度量，在训练集T中找出与x最邻近的k个点。

(2)    对k个点根据分类决策规则（如多数表决）决定x的类别y：

 

I是指示函数，即当时yi=cj时I为1，否则为0。直观表达如下图：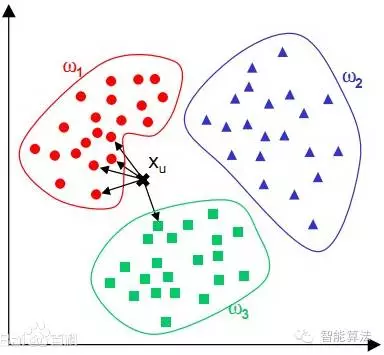
二、基本要素

距离度量：特征空间中的两个实例的距离是两个实例点相似程度的反映，k-NN模型通常使用的是欧氏距离，但也可以选用其它距离，如曼哈顿距离、切比雪夫距离和闵可夫斯基距离等。

k值的选择：k值的选择对于k-NN的结果有重大影响，如果选择较小的k值，相当于用较小的领域中的训练实例进行预测，此时预测结果对近邻的实例点非常敏感，如果实例点恰巧是噪声，预测就会出错，也就是说，k值越小，整体的模型越复杂，模型容易出现过拟合现象。k=1的情况被称为最近邻算法。如果选择较大k值，相当于用较大领域中的训练实例进行预测，此时容易出现一些较远的训练实例（不相似的）也会对预测起作用，k值得增大就意味着整体模型变简单了。k=N时会出现模型将输入实例简单的预测属于训练实例中最多的类。因此在应用中，k一般取较小的数值，通常采取交叉验证法选取最优的k值。

分类决策规则：k-NN中的分类决策规则一般选择多数表决，即输入实例的k个邻近的训练实例中多数类决定输入实例的类。

三、算法实现

算法步骤：

step.1---初始化距离为最大值

step.2---计算未知样本和每个训练样本的距离dist

step.3---得到目前K个最临近样本中的最大距离maxdist

step.4---如果dist小于maxdist，则将该训练样本作为K-最近邻样本

step.5---重复步骤2、3、4，直到未知样本和所有训练样本的距离都算完

step.6---统计K-最近邻样本中每个类标号出现的次数

step.7---选择出现频率最大的类标号作为未知样本的类标号

python代码实现如下：

四、算法优化

实现k-NN近邻时，主要考虑的问题是如何对训练数据进行快速搜索，这点对于维数大及训练数据容量大的特征空间尤为重要，k-NN最简单的实现方法是线性扫描，即计算每个输入实例和训练实例的距离，训练集很大时，非常耗时，也失去了本身的意义。为了提高k近邻的搜索效率，可以采用kd树，由于篇幅先不讨论kd树，以后再写，另外一点，我们在使用k-NN时可能会选择距离太远的近邻，这些与输入实例的相似性较低，因此一种补偿方法是根据距离的远近为其赋予相应的权重，有三种常用获取权重的方法。

1．  反函数

取距离的反函数作为权重，最简单的方式是取距离的倒数，但是存在一个问题，当出现完全一样或非常近的实例时，会使得权重非常的大，甚至无穷，基于此，对距离取导数前加上一个较小的常数。

2．  减法函数

用一个常数值减去距离，如果相减的结果大于0，则权重为相减的结果，否则，结果取0，该方法很好的克服了权重分配过大的问题，但也存在一些局限，由于权重限定一定距离的实例，因此可能我们找不到足够近的项视为近邻，即对于一些实例，无法做预测。

3．高斯函数

      该方法是根据高斯函数取权重，在距离为0的时候权重为1，并且权重随着距离的增加而减小，和减法函数不同的是，权重不会出现跌至到0，很好的克服了前两个函数的局限，不过相对复杂一些，使得执行速度没有前两个函数快。

五、算法的优缺点

k-NN能够利用复杂函数进行数值预测，同时又保持简单易懂的特点，它是一种在线（online）技术，也就是说，新的数据可以在任何时候不需要进行任何计算，直接将数据添加到集合即可。

k-NN主要的缺点是为了完成预测，所有的训练集数据都必须缺一不可，当面对百万样本的数据集，在空间上和时间上都存在着问题。