机器学习：朴素贝叶斯算法实现垃圾邮件分类

一.基于贝叶斯决策理论的分类方法

朴素贝叶斯：

优点：在数据较少的情况下仍然有效，可以处理多类别问题

缺点：对于输入数据的准备方式较为敏感

适用性数据类型：标称型数据

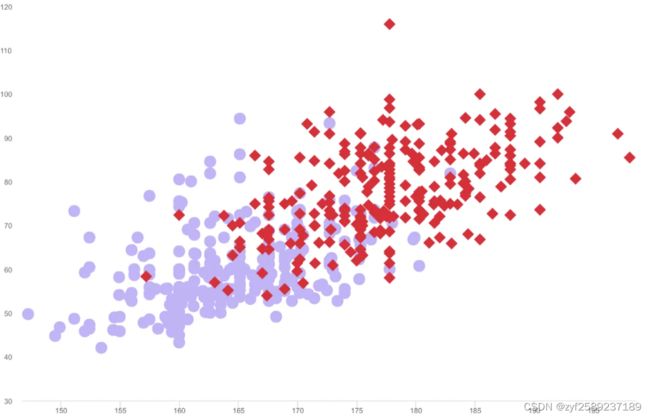
        朴素贝叶斯是贝叶斯决策理论的一部分，所以讲朴素贝叶斯之前有必要快速了解一下朴素贝叶斯决策理论。假设现在有一个数据集，它由两部分数据组成，如图所示：

现在我们用p1（x，y）表示数据点（x，y）属于类别1（图中用紫色的点表示的类别）的概率，用p2（x，y）表示数据点（x，y）属于类别2（图中用红色的点表示的类别）的概率，那么对于一个新数据点（x，y），可以用下面的规则来判断它的类别：

        如果p1（x，y）>p2（x，y），那么为类别1.

        如果p2（x，y）>p1（x，y），那么为类别2.

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。接下来，我们有必要详述p1和p2的概率计算方法。为了能够计算p1与p2，需要引入条件概率的概念。

二.条件概率

条件概率是指事件A在事件B发生的条件下发生的概率。条件概率表示为：P（A|B），读作“A在B发生的条件下发生的概率”。若只有两个事件A，B，那么

                        ​​​​​​​        ​​​​​​​        ​​​​​​​        

一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果，及如果知道P（x|c）,要求P(c|x)，呢么可以使用下面的计算方法：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

P(c) 称为”先验概率”，即在x事件发生之前，我们对c事件概率的一个判断。如：正常收到一封邮件，该邮件为垃圾邮件的概率就是“先验概率”
P(c|x)称为”后验概率”， 即在x事件发生之后，我们对c事件概率的重新评估。如：邮件中含有“中奖”这个词，该邮件为垃圾邮件的概率就是“后验概率”

接下来的问题就是将其应用到分类器中。

三.使用条件概率分类

前面提到贝叶斯决策理论要求计算两个概率p1（x，y）和p2（x，y）：

        如果p1（x，y）>p2（x，y），那么为类别1.

        如果p2（x，y）>p1（x，y），那么为类别2.

但这两个准则并不是贝叶斯决策理论的所有内容。真正需要计算和比较的是p（c1|x,y）和

p（c2|x,y）。注意这邪恶概率与刚才给出的概率p（x，y|c1）不一样，不过可以使用贝叶斯准则来交换概率中条件与结果。应用贝叶斯准则得到：

 

使用这些定义，可以定义贝叶斯分类为：

        如果p（c1|x，y）>p（c2|x，y），那么为类别c1.

        如果p（c1|x，y）

 使用贝叶斯准则，就可以通过已知的三个概率值来计算位置的概率值。

四.使用朴素贝叶斯进行分类

朴素贝叶斯的一般过程：

1.收集数据：可以使用任何方法。

2.准备数据：需要数值型或者布尔型数据。

3.分析数据：有大量特征时，绘制特征作用不大，此时使用直方图效果更好。

4.训练算法：计算不同的独立特征的条件概率。

5.测试算法：计算错误率。

6.使用算法：一个常见的朴素贝叶斯应用时文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器，不一定非要是文本。

五.实例

Python实现：（完整代码）

import os
import re
import string
import math

DATA_DIR = 'text'
target_names = ['ham', 'spam']

#数据读取
def get_data(DATA_DIR):
    subfolders = ['text%d' % i for i in range(1, 5)]
    data = []
    target = []
    for subfolder in subfolders:
        # spam
        spam_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'spam'))
        for spam_file in spam_files:
            with open(os.path.join(DATA_DIR, subfolder, 'spam', spam_file), encoding="latin-1") as f:
                data.append(f.read())
                target.append(1)
        # ham
        ham_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'ham'))
        for ham_file in ham_files:
            with open(os.path.join(DATA_DIR, subfolder, 'ham', ham_file), encoding="latin-1") as f:
                data.append(f.read())
                target.append(0)
    return data, target


X, y = get_data(DATA_DIR)

#数据预处理
class SpamDetector_1(object):

    # 清除空格
    def clean(self, s):
        translator = str.maketrans("", "", string.punctuation)
        return s.translate(translator)

    # 分开每个单词
    def tokenize(self, text):
        text = self.clean(text).lower()
        return re.split("\W+", text)

    # 计算某个单词出现的次数
    def get_word_counts(self, words):
        word_counts = {}
        for word in words:
            word_counts[word] = word_counts.get(word, 0.0) + 1.0
        return word_counts

#数据处理
class SpamDetector_2(SpamDetector_1):
    # X:data,Y:target标签（垃圾邮件或正常邮件）
    def fit(self, X, Y):
        self.num_messages = {}
        self.log_class_priors = {}
        self.word_counts = {}
        # 建立一个集合存储所有出现的单词
        self.vocab = set()
        # 统计spam和ham邮件的个数
        self.num_messages['spam'] = sum(1 for label in Y if label == 1)
        self.num_messages['ham'] = sum(1 for label in Y if label == 0)

        # 计算先验概率，即所有的邮件中，垃圾邮件和正常邮件所占的比例
        self.log_class_priors['spam'] = math.log(
            self.num_messages['spam'] / (self.num_messages['spam'] + self.num_messages['ham']))
        self.log_class_priors['ham'] = math.log(
            self.num_messages['ham'] / (self.num_messages['spam'] + self.num_messages['ham']))

        self.word_counts['spam'] = {}
        self.word_counts['ham'] = {}

        for x, y in zip(X, Y):
            c = 'spam' if y == 1 else 'ham'
            # 构建一个字典存储单封邮件中的单词以及其个数
            counts = self.get_word_counts(self.tokenize(x))
            for word, count in counts.items():
                if word not in self.vocab:
                    self.vocab.add(word)  # 确保self.vocab中含有所有邮件中的单词
                # 下面语句是为了计算垃圾邮件和非垃圾邮件的词频，即给定词在垃圾邮件和非垃圾邮件中出现的次数。
                # c是0或1，垃圾邮件的标签
                if word not in self.word_counts[c]:
                    self.word_counts[c][word] = 0.0
                self.word_counts[c][word] += count


MNB = SpamDetector_2()
MNB.fit(X[100:], y[100:])

#测试
class SpamDetector(SpamDetector_2):
    def predict(self, X):
        result = []
        flag_1 = 0
        # 遍历所有的测试集
        for x in X:
            counts = self.get_word_counts(self.tokenize(x))  # 生成可以记录单词以及该单词出现的次数的字典
            spam_score = 0
            ham_score = 0
            flag_2 = 0
            for word, _ in counts.items():
                if word not in self.vocab:
                    continue

                # 下面计算P(内容|垃圾邮件)和P(内容|正常邮件),所有的单词都要进行拉普拉斯平滑
                else:
                    # 该单词存在于正常邮件的训练集和垃圾邮件的训练集当中
                    if word in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log(
                            (self.word_counts['spam'][word] + 1) / (
                                        sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log(
                            (self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
                                self.vocab)))
                    # 该单词存在于垃圾邮件的训练集当中,但不存在于正常邮件的训练集当中
                    if word in self.word_counts['spam'].keys() and word not in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log(
                            (self.word_counts['spam'][word] + 1) / (
                                        sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log(1 / (sum(self.word_counts['ham'].values()) + len(
                            self.vocab)))
                    # 该单词存在于正常邮件的训练集当中,但不存在于垃圾邮件的训练集当中
                    if word not in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log(1 / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log(
                            (self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
                                self.vocab)))

                # 把计算到的P(内容|垃圾邮件)和P(内容|正常邮件)加起来
                spam_score += log_w_given_spam
                ham_score += log_w_given_ham

                flag_2 += 1

                # 最后，还要把先验加上去，即P(垃圾邮件)和P(正常邮件)
                spam_score += self.log_class_priors['spam']
                ham_score += self.log_class_priors['ham']

            # 最后进行预测，如果spam_score > ham_score则标志为1，即垃圾邮件
            if spam_score > ham_score:
                result.append(1)
            else:
                result.append(0)

            flag_1 += 1

        return result


MNB = SpamDetector()
MNB.fit(X[100:], y[100:])
pred = MNB.predict(X[:100])
true = y[:100]

accuracy = 0
for i in range(100):
    if pred[i] == true[i]:
        accuracy += 1
print("识别准确率为：",accuracy)

运行结果：

六.小结

        对于分类而言，使用概率有时要比使用应规则更有效。贝叶斯概率及贝叶斯准则提供了一种利用已知值来估计位置概率的有效方法。