PL-SLAM论文翻译

声明：该翻译不是我的工作，来自乔志健  https://github.com/qiaozhijian/PL_SLAM 

写在这里，感谢该作者。这个论文说了啥呢？就是说原来做ORB_SLAM一般都是采用特征点作为连续位姿变换的依据，PL_SLAM 增加了线特征，这样就在特征点少而有线特征的环境中具有了一定的稳健性!那个“鲁棒性”就是稳健性！在稀疏地图构建上也有了一些线特征。整体上这个论文工作很有意义，比单纯的点特征增加一维线特征，当然很有意义啦！真正的机器人应用肯定是双目的好啦，大家如果面向实际应用，还是研究双目的好。这里不粘贴图片了，原文在以上链接也有，再次谢谢这些传播者！同时引述分析一下SLAM所谓的特征点法语直接法优缺点：http://bat.sjtu.edu.cn/zh/shuangmu/

在视觉SLAM领域中按照误差方程的不同可以分为特征点法的视觉SLAM和直接法的视觉SLAM，比如PTAM(http://www.robots.ox.ac.uk/~gk/PTAM/) 和ORB-SLAM (http://webdiis.unizar.es/~raulmur/orbslam/)都是经典的特征点法SLAM，而DSO(https://vision.in.tum.de/research/vslam/dso)和LSD-SLAM(https://vision.in.tum.de/research/vslam/lsdslam)为经典的直接法SLAM。特征点法和直接法各有优缺点，具体如下表一所示

表一 特征点法和直接法优缺点对比表

	优点	缺点
特征点法	即使相邻帧运动过大，也能很好地tracking	计算特征点和描述子耗时
	原生支持回环检测	只能构建稀疏地图
	相机的自动曝光影响较少，并且对双目比较友好	场景要求高，需要大量不同角点
直接法	无需计算特征点和描述子	回环检测和全局优化较困难
	对场景要求宽松，只需要有梯度变化，无需角点	基于灰度不变的假设，相机的曝光会影响结果，并且对双目不友好
	可以构建半稠密或稠密地图	非凸性较强，相邻帧运动过大容易陷入局部最优

基于直接法的SLAM由于没有特征点的支持，因此无法实现SLAM中的回环检测功能，而回环检测功能又是SLAM中消除累计误差的一个重要功能，因此我们在DSO的基础上增加了回环检测方法。此外直接法多用于单目视觉的计算，没有实际的物理尺寸，我们添加了双目传感器，并基于双目实现了带有物理尺度的直接法SLAM。

PL-SLAM：a Stereo SLAM System through the Combination of Points and Line Segment

Ruben Gomez-Ojeda, David Zuñiga-Noël, Francisco-Angel Moreno,
Davide Scaramuzza, and Javier Gonzalez-Jimenez

  摘要——传统的立体视觉SLAM方法依靠点特征去估计相机轨迹和构建环境地图。然而在弱纹理环境里，找到足够多可靠点特征通常是一件很难的事，这导致传统方法的性能会降低。本文提出了PL-SLAM，一种结合点和线段特征的立体视觉SLAM系统，能够在鲁棒地在更多不同的场景里运行，比如特征点稀少或图像特征分布不均匀的场景。PL-SLAM在视觉里程计，关键帧选取，BA等所有的过程里利用点和线段特征。我们也充分利用了点线特征组合描述的优点，去设计了一种新型的词袋法，用于回环检测中。此外，由此得来的3D地图更加丰富并且多样，可被利用与测量有价值的高级的场景结果，比如面，空旷的空间，地面等（本文中没有提到）。我们的想法在数个公共数据集（KITTI和EuRoC）上进行了测试，并且和最先进的方法如ORB-SLAM进行了比较——我们可以在大部分环境里表现得更鲁棒的同时保证算法的实时性。并且，为了造福研究社区，我们发布了一个开源的用C++编写的PL-SLAM项目。

关键词——立体视觉SLAM，线段特征，光束平差法，回环检测

I. 介绍

  近年来，视觉实时同步定位与建图（SLAM）稳固地提升了需要这项技术的全自动车辆，例如移动机器人，自动驾驶骑车或无人机，的可靠性。简而言之，SLAM的问题在于给定一系列的位置和姿态作为车辆轨迹的估计，以及实时构建环境的地图。且不说自定位，地图就对避障，物体检测，任务规划等部分很有帮助【1】。

  SLAM系统首先可被分为两大类，基于拓扑（例如【2】-【5】）和度量的方法。本文，我们关注后者，并考虑环境的几何信息，构建一个有物理意义的地图【6】，【7】。这又能分为直接法和特征点法两种。第一种，直接法，假设空间的局部块的像素光度不变，然后最小化连续两帧间光度误差去估计相机的位姿（这个方法的例子可以在别处找到，如【8】-【10】）。虽然这种方法并没有利用一些中间变量而是直接利用输入图像的信息工作，但它对光照变化很敏感（这个现象在【11】中有提到），并且只能用于较小的运动（baseline？）里。相对地，基于特征的方法采用非直接的图像表示，尤其是以点特征的形式，去跟踪连续帧并通过最小化投影误差【12】【13】恢复位姿。

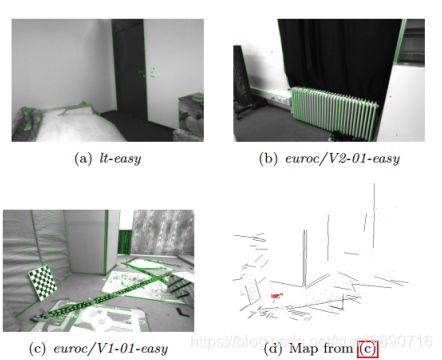
  显而易见，上述提到的任何一个方法都会由于难以发现足够多的关键点特征而在弱纹理环境中表现不佳。这些情况会导致精度的降低，甚至有时导致整个系统的崩溃。然而，许多弱纹理特征却包含线特征丰富的面，因此从中提取线段是可行的。我们认为，两种特征（点和线）相互补充，并且两者结合会构建一个更通用鲁棒稳定的SLAM系统。另外，其产生的地图同时包含3D点和线段，会比基于点特征构建的地图提供更多的环境结构信息，这在图一的（d）部分可以看到。因此，一些用于完成高水平任务，如位置识别，语义地图或任务规划的应用将从这种地图中提取更丰富的信息，从而受益于此。

  但是，伴随这些好处而来的是更高的计算成本，如检查和匹配图像中的线段特征【14】，又如处理一些如部分遮挡，线段断开等针对于线段的问题，这些都使特征的跟踪，匹配以及地图和位姿优化的残差计算复杂化。正是由于这些障碍，一些结合线特征的SLAM和SfM文献受限了。除此之外，我们也很少发现只在高结构化环境鲁棒在现实场景如KITTI或EuRoC数据集表现不佳的方法。在这项工作中，我们通过比较线段特征的长度和方向去丢弃不正确的特征，以此解决针对线段的特征跟踪和匹配问题。同时，对于残差计算，我们用线段的端点坐标去表示地图中的线段，通过计算线段端点在图像上的投影到被观测无限长线段的距离，去计算观测到的线段和与之对应的地图的线段的残差。通过这种方式，我们构建了一个包含点线特征的一致的误差函数。

 

图1 弱纹理环境对基于特征点的SLAM系统是很有挑战性的。相反，线段常常存在与人造环境中，它不仅会提升相机定位的效果，以次构建的地图也会拥有更有丰富更有意义的信息（3D线段）。

 

  通过一种新型的结合点线特征优势去进行位置识别的词袋法，这两种特征在机器人导航里被应用于鲁棒地检测回环。总的来说，我们基于我们之前做过的视觉里程计方法【20】，提出了一种新型通用的几何点线特征名为PL-SLAM的SLAM系统，并用于实时机器人定位和地图构建。我们工作的主要贡献如下：

  1. 第一次给出了可实时运行的开源的联合点线特征双目视觉SLAM系统，不同于其他传统仅仅基于点特征的方法，该系统能够稳定地在弱纹理环境中运行。同时，该系统也能在其他环境场景中取得与传统方法精度相当的结果。由于联合考虑了点线特征，本文提出的方法所创建的地图包含更为丰富的几何特征。

  2. 提出了关于光束平差过程的一种新的实现途径，即在优化关键帧位姿时不间断地对两种特征进行说明。

  3. 通过同时考虑点线特征的描述，对文献【21】提出的词袋方法进行了拓展，从而进一步改善回环检测过程。

讲解视频见http://mapir.uma.es，开源项目见https://github.com/rubengooj/pl-slam。

 

II. RELATED WORK

III. PL-SLAM OVERVIEW

  PL-SLAM大体结构由图二描述，同时主要模块由以下的小节描述。正如其他SLAM系统一样（当今最流行的方案ORB-SLAM【13】），我们方案也基于三个不同的线程：视觉里程计，局部建图和回环检测。这种高效的分配方式使得VO模块能（对相机位姿和地图）进行连续跟踪，同时当关键帧插入时，对回环检测和局部地图线程进行处理。

 

图2. PL-SLAM结构图

  地图。地图由i)一系列关键帧（KFs），ii）被检测到的3D路标（点和线段），iii）一个共视图和iv）一个生成树构成。

  关键帧包含被观测的立体特征和他们的描述子，一个左图与之对应的通过一个视觉词典（在VI-A小节会讲到）计算的的视觉描述子，和相机3D位姿。

  关于路标，我们为每个路标储存一系列的观测（观测到该路标的帧？）以及最典型的描述子。除此之外，针对点，我们保存它被估计的3D位置，针对线，我们保存它的方向和端点的3D坐标。

  最后，可视信息，如【38】，被一个图建模：每个节点代表一个关键帧，两个关键帧之间的边仅当两帧至少看见一定数目（我们的研究默认为20个，例如图3）的路标点才建立，这允许我们能实时用BA处理局部地图。

  同样地，为了实现更快的回环检测优化，我们也用了所谓的essential graph，它仅在两帧间共视地标点超过100个时才在两帧间建立边，因此没有共视图稠密。最后，地图也包含一个生成树，它是包含所有关键帧的最小的一个图。

 

图3 lt-first序列的共视图，绿线代表两帧间的边

  特征跟踪。在我们先前的工作中，我们基于双目视觉里程计算法完成了特征跟踪【20】。简而言之，我们从一系列的双目帧里跟踪图像特征（点和线），并计算他们的3D位置和用协方差矩阵表示的不确定性。然后，3D路标被投影到新的相机位姿下，接着最小化投影误差以获得相机位姿增量和此次估计的不确定性。直到一个新的关键帧被插入之前，这个过程在每个新的帧到来时都重复一遍，执行者简易的帧到帧的VO过程。更深的特征跟踪过程会被第IV小节正式描述。一旦关键帧被插入地图，局部建图和回环检测将同时进行。

  局部建图。局部地图线程会去查找新的关键帧和上一个关键帧以及共视图中与上一个关键帧连接的帧之间的新的特征匹配。通过这种方式，我们构建当前关键帧所谓的局部地图，其中报告当前关键帧以及所有与其共视至少20个路标的关键帧，以及被它们观测到的所有路标。最后，局部地图中的所有元素（关键帧和路标）一起参与优化。第V小节会展示详细过程。

  闭环检测。闭环检测线程平行于局部地图线程进行，它通过基于词袋法（第VI小节会描述）提取视觉特征而执行。在相机移动过程中，所有被捕获帧的视觉描述子都会存储在一个数据库里，用来和当前帧进行比较，从而选出一系列相似的帧。仅当围绕该KF的局部序列也是相似的（？），我们才把最佳匹配帧作为回环检测的一个候选。最后，我们估计匹配帧和当前帧的相对位姿SE（3），如果估计是合理的，那么所有的关键帧都将参与位姿图（PGO）而进行优化。

  我们需要注意，双目视觉里程计在每个帧都在运行，而回环检测和局部建图（分离的两个线程）则是仅当关键帧插入时才在后台运行的，这是很重要的，因为这保证了我们系统的实时性。万一局部地图线程正在进行时，一个关键帧突然插入，那么这个关键帧将被临时保存，知道局部建图线程结束，我们再开启一个新的局部建图命令。

  这些建图和回环检测方法和下文提到的ORB-SLAM里的是一样的，它们都旨在降低一般BA（还有近年来的稀疏代数技术的合并？）带来的高计算成本。在BA框架里，我们的方案属于可替代运算成本较高的全局方法（例如【24】，【42】）的所谓的相对（relative）技术（例如【39】-【41】）。

 

IV. 特征跟踪

  这个部分综述了我们先前工作【20】最重要的几个部分，包括连续帧间的视觉里程计和关键帧选取策略。基本上，点和线段通过一系列双目帧进行跟踪（见图一），然后相机的3D运动（以及它的不确定性）通过最小化投影误差而被计算。

 

A. 点特征

  本次工作中，鉴于ORB【27】方法优秀的关键点检测性能，以及它所提供的二进制描述子能更高效地完成关键点匹配，我们选用这个著名的点特征方法。为了减少异常点的数量，我们仅考虑那些同时在左右图像都是最有匹配的点，换句话说，他们互相为最有匹配。最后，我们也过滤掉那些与第二最有匹配在描述子空间的距离小于与最有匹配的距离的两倍的匹配以保证匹配足够有意义。（？）

B. 线段特征

  线段特征检测器（LSD【37】）用于提取线段，这种方法精度高，重复性好。为了双目匹配和帧间跟踪，我们使用线带描述器（LBD【43】）额外加入了线段的二进制描述子，这帮助我们在他们的局部外形基础上进行线段匹配。同样对于这些点，我们也会检查它们是否互相为最佳匹配以及是否有意义。最后，我们利用线段提供的有用的几何信息去过滤掉那些不同方向和长度或者端点不一致的线匹配。要注意，这个滤波器帮助系统去保持更多的结构线，有利于基于点线的地图的一致性（见图一（d））。

 

C. 运动估计

  一旦我们建立了两个双目帧之间的匹配关系，我把点线特征从第一帧反投影到下一帧上。然后，我们基于高斯牛顿迭代法，最小化特征点和特征线的投影误差去求得帧间运动。为了处理异常点，我们使用Pseudo-Huber损失函数并执行一个两步最小化（？），正如【44】所提到的那样。最后，我们得到了连续两帧间被估计位置的增量，这可用下式建模：

 

这里是从帧t到帧t+1的一个六维相机位姿向量，并且代表被估计运动的协方差矩阵，以代价函数最后一次迭代的海塞矩阵H的逆来近似。

 

D. 关键帧选取

  为了决定一个新的关键帧何时被插入到地图里，我们遵从【45】中的方法，采用了有关运动估计的不确定性。因此，紧接着等式（1），我们把不稳定性从协方差矩阵转换成一个叫做熵的标量，通过下面的表达式：

 

然后，对于一个被给定的关键帧i，我们会去计算当前帧Fi+u与关键帧i的熵的比值，再与关键帧i与它下一个帧i+1的熵的比值比较，例如：

 

如果α的值小于被预先设定好的阈值（我们的实验里设置为0.9），那么当前帧Fi+u会被作为一个新的关键帧插入到系统里。并且注意到，为了计算表达式（2），我们需要知道非连续帧的位姿增量的不确定性，但等式（1）值估计了连续帧间的位姿增量的不确定性。这一系列的估计由一阶高斯传播法（？）完成，以得到非连续关键帧间的不确定性。

 

V. 局部建图

  这部分描述了当一个关键帧被插入时的系统行为。本质上说，就是说执行了所谓的局部地图的BA，进一步说，局部地图是指当前帧和共视图上与其连接的帧以及所有被这些局部帧观测到的路标。

 

A. 关键帧插入

  每当视觉里程计选择一个关键帧，我们把它插入到SLAM系统里并优化局部地图。首先，我们改善了当前帧和之前关键帧的位姿变化估计，因为由VO提供的帧是通过组合中间帧的相对运动而被估计的。为此，我们构建关键帧之间的数据关联，考虑第IV部分描述的几何约束，并得到一个系列被他们观测的公共特征。然后，我们执行一个类似的优化，就像我们在IV-C部分展示的那样，并且，我们把VO部分提供的位姿作为高斯牛顿最小化方法的初始值。一旦我们计算出关键帧之间的相对位姿变化，我们把当前帧插入系统中，包括：

  1）关键帧索引。

  2）3D位姿的信息，包含一个绝对位姿，相对于上一个关键帧的位姿以及不确定性。

  3）新的3D路标，并以储存对应的2D像素坐标和描述子的形式初始化。已存在的路标的新观测也会被加入到地图里。

最后，我们也在当前帧的未匹配的特征观测和局部地图的路标点里里寻找新的对应关系。

 

B. 局部光束平差法

  在插入关键帧之后，下一步就是进行局部地图的BA。正如前文所说，局部地图是由当前帧和共视图上与其连接的帧（共视至少20个路标）以及所有被这些局部帧观测到的路标组成。为此，我们定义向量ψ为所有要优化的量的集合，其中包含se（3）形式关键帧位姿量，3D点位置，以及每条线段的3D端点坐标。（w应该代表世界坐标系，i，j，k代表索引，）然后，我们最小化观测和路标投影到观测它们的帧上的坐标的投影误差，如下所示：

 

其中分别代表关键帧组，路标点组，路标线组。

  在下面表达里，投影误差eij描述了第j个地图点在第i个关键帧的投影与实际观测的2D距离，能被如下表达式描述：

 

其中，π代表世界坐标系下的第j个3D坐标点坐标在局部参考系第i个关键帧的坐标Xij，然后在投影到像素坐标系。对于线段而言，有些许不同，我们不能简单地比较端点坐标的不同，因为在一帧到另一帧的过程中，他们很可能出现在线上的不同位置或者被挡住。为此，我们去计算3D线段在图像上的端点到与之对应的直线在图像平面上投影的距离，以此作为误差函数。这样，第i个帧观测的第k个线段的误差eik就可以被给定为：

 

其中P和Q代表世界坐标系中的3D端点坐标，lik是第i个关键帧观测的第k个线段所对应的直线方程，这可以由齐次坐标系下的线段2D端点的叉乘得到，例如。

  （4）中的问题能够通过以下的L-M方法迭代被解决，为此我们需要同时估计雅可比矩阵和海塞矩阵：

 

其中，误差向量e包含所有投影误差eij和eik。下面的等式展示了更新过程：

 

通过迭代，我们会收敛到最优ψ，由此更新局部关键帧和路标。注意，由于ψ的变量的不同性质，更新式不是直接应用于整个向量的。

  值得一提的是，每个观测误差eij和eik仅仅去取决于一个单独的关键帧位姿和一个单独的路标。因此，海塞矩阵能够通过附加每个观测对它对应的矩阵区块的影响而构成，正如等式（9）展现的那样。注意，对于剩余的不属于局部地图的关键帧，他们的雅克比矩阵为0，因为我们只优化局部地图，而认为其他的关键帧的位姿是固定的。

  同时也需要强调，在（4）中，点和线的误差的影响分别被各自不稳定性的协方差矩阵的逆和加权了。实际上，把这些协方差矩阵直接设置成单位矩阵，相对于IV-C部分提出的方法是更有效的。因为它引进了鲁棒的权重，同时也处理了异常点观测。（？）

  最后，我们把地图上少于三个观测的路标移除，因为它们的意义并不是很大。