A Robust Fuzzy Local Information C-means Clustering Algorithm

鲁棒的模糊局部信息C均值聚类算法

摘要

本文提出了一种模糊c均值（FCM）算法的变体，该算法可提供图像聚类。该算法以一种新颖的模糊方式融合了局部空间信息和灰度信息。新算法称为模糊局部信息C均值（FLICM）。 FLICM可以克服已知的模糊c均值算法的缺点，同时可以提高聚类性能。 FLICM的主要特征是使用模糊局部（空间和灰度）相似性度量，旨在确保对噪声不敏感并保留图像细节。此外，所提出的算法完全没有经验调整的参数（α，λg，λs等）并入文献中提出的所有其他模糊c均值算法中。对合成和真实世界图像进行的实验表明，FLICM算法是有效且高效的，可为嘈杂的图像提供鲁棒性。
索引词-模糊c均值，聚类，图像分割，空间约束，灰度约束，模糊约束。

一，引言

图像分割是图像分析和计算机视觉中最重要的任务之一。在文献中，已经提出了用于对象分割和特征提取的各种方法，在[1]，[2]中进行了描述。然而，由于图像的多样性和复杂性，鲁棒和高效的分割算法的设计仍然是一个非常具有挑战性的研究课题。图像分割被定义为将图像划分为在某些特性（例如强度，颜色，色调，纹理等）方面相同的非重叠，一致的区域。图像分割可以分为四类：阈值处理，聚类，边缘检测和区域提取。在本文中，将考虑一种用于图像分割的聚类方法。
聚类是一种以这样一种方式对对象或模式进行分类的过程，即与属于不同聚类的样本相比，同一聚类的样本彼此之间更加相似。主要有两种聚类策略：硬聚类方案和模糊聚类方案。常规的硬聚类方法仅将数据集的每个点分类为一个聚类。结果，结果通常非常清晰，即在图像聚类中，图像的每个像素仅属于一个聚类。但是，在许多实际情况下，诸如空间分辨率有限，对比度差，强度重叠，噪声和强度不均匀性之类的问题降低了硬（脆性）聚类方法的有效性。模糊集理论[3]引入了部分隶属度的概念，用隶属度函数描述。模糊聚类作为一种软分割方法，已经得到了广泛的研究，并成功地应用于图像聚类和分割[4]，[5]，[6]，[7]，[8]，[9]。在模糊聚类方法中，模糊c均值（FCM）算法[10]是图像分割中使用最广泛的方法，因为它具有较强的歧义性，并且比硬分割法[11]保留更多的信息。尽管常规FCM算法在大多数无噪声的图像上都能很好地工作，但是它对噪声和其他成像伪影非常敏感，因为它不考虑有关空间上下文的任何信息。
为了弥补FCM的这一缺点，在[9]，[12]，[13]中提出了预处理图像平滑步骤。但是，通过使用平滑滤镜，可能会丢失重要的图像细节，尤其是边界或边缘。而且，没有办法控制平滑和聚类之间的折衷。因此，许多研究人员已经将局部空间信息纳入原始FCM算法中，以提高图像分割的性能[5]，[11]，[14]。
Tolias和Panas [5]开发了一种基于模糊规则的方案，称为基于规则的邻域增强系统，通过对FCM聚类结果进行后处理来施加空间约束。
Noordam等人[6]提出了一种几何指导的FCM（GG-FCM）算法，一种半监督的FCM技术，其中通过考虑每个像素的局部邻域来确定几何条件。
Pham [15]修改了FCM目标函数，包括对隶属函数进行空间惩罚。惩罚项导致了一个迭代算法，该算法与原始FCM非常相似，并允许估计空间平滑的隶属函数。
Ahmed等人[9]提出了FCM_S，其中对经典FCM的目标函数进行了修改，以补偿强度的不均匀性，并允许像素的标记受到其紧邻像素的影响。 FCM_S的一个缺点是在每个迭代步骤中都要计算邻域标签，这非常耗时。
Chen和Zhang [12]提出了FCM_S算法的两个变体FCM_S1和FCM_S2，以减少计算时间。这两种算法分别引入了额外的均值和中值滤波图像，这些图像可以预先计算，以代替FCM_S的邻域项。因此，FCM_S1和FCM_S2的执行时间都大大减少了。
Szilagyi等人[13]提出了增强的FCM（EnFCM）算法来加速图像分割过程。 EnFCM的结构不同于FCM_S及其变体。 首先，由原始图像和每个像素的局部邻域平均灰度级形成线性加权和图像。 然后，基于灰度直方图而不是求和图像的像素执行聚类。 由于图像中的灰度级数通常比其像素数小得多，因此减少了EnFCM算法的计算时间，而分割后的图像的质量可与FCM_S相比[13]。
最近，Cai等人[16]提出了一种快速通用的FCM算法（FGFCM），该算法结合了空间信息，局部像素邻域的强度和图像中的灰度级数。该算法从原始图像及其局部空间和灰度邻域形成非线性加权和图像。由于基于灰度直方图进行聚类，因此FGFCM的计算时间非常短。分割图像的质量得到了很好的增强[16]。
但是，EnFCM和FGFCM具有相同的关键参数a（或λ）。此参数用于控制原始图像及其对应的均值或中值滤波图像之间的折衷。它对这些方法的性能具有至关重要的影响，但是通常很难选择它，因为它应该在对噪声的鲁棒性和保留细节的有效性之间保持平衡。换句话说，必须选择足够大的a值以容忍噪声，另一方面，必须选择足够小的a值以保持图像的清晰度和细节[13]。因此，我们可以得出结论，a的确定实际上在某种程度上取决于噪声。由于图像噪声的种类通常是先验未知的，因此，在实践中通常通过反复试验[9]，[12]，[13]通过实验来选择a（或λ）。而且，对于图像上的所有像素邻域，a（或λ）的值是固定的。
本文处理上述问题。它提出了一种新颖的鲁棒的模糊局部信息cmeans聚类算法FLICM，该算法可以处理参数a（或λ）选择的缺陷，并提高图像分割性能。在FLICM中，定义了一种新颖的模糊因子来替换EnFCM和FCM S及其变体中使用的参数a和FGFCM及其变体中使用的参数λ。新的模糊局部邻域因子可以自动确定空间和灰度关系，并且完全不需要任何参数选择。因此，FLICM具有以下吸引人的特征：1）它相对独立于噪声的类型，因此，在没有先验噪声知识的情况下，它是进行聚类的更好选择； 2）模糊局部约束以模糊方式同时合并了局部空间和局部灰度关系； 3）可以自动确定模糊局部约束，因此不需要任何参数确定； 4）通过模糊的局部约束自动实现图像细节和噪点之间的平衡，同时增强了聚类性能。所有这些特性使FLICM变得更加通用，适合图像聚类算法。
在本文的其余部分安排如下。第二部分简要介绍了具有空间约束的模糊c均值聚类算法（FCM S，FCMS1和FCMS2），然后介绍了EnFCM和FGFCM算法。第三节介绍了FLICM算法。实验结果在第四节中给出，结论在第五节中得出。

二。 初步理论

A.模糊C均值（FCM）算法

模糊c均值（FCM）聚类算法由Dunn [17]首次提出，后来由Bezdek [10]扩展。 该算法是一种迭代聚类方法，它通过最小化平方误差目标函数Jm [10]的组和内的加权来产生最佳c分区：

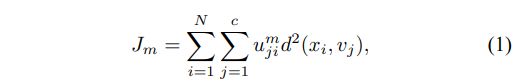
其中X = {x1，x2，。 。 。 ，xN}⊆IRm，是m维向量空间中的数据集，N是数据项的数量，c（2≤c 1）设定c，m和ε的值，
2）初始化模糊分区矩阵U（0），
3）设置循环计数器b = 0，
4）用U（b）计算c个聚类中心v（b）j：

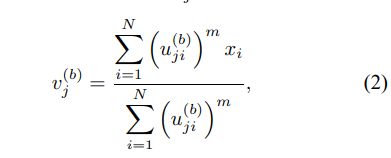
5）计算隶属度矩阵U（b + 1）：

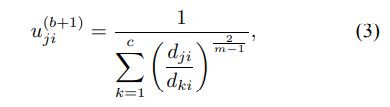
6）如果max {U(b)-U(b + 1)}<ε则停止，否则，设置b=b+1并转到步骤4。

B.带约束的模糊聚类（FCM S）及其变体

Ahmed等[9]提出了对标准FCM的修改，引入了一个项，该项允许像素的标记受到其紧邻像素的影响。 邻域效应充当正则化器，并使解决方案偏向分段均质标记。 FCM_S的修改后的目标函数定义如下：

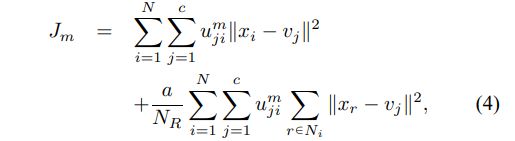
其中xi是第i个像素的灰度值，N是像素总数，vj是第j个中心的原型值，uji表示第i个像素相对于聚类j的模糊隶属关系，NR是 其基数,xr代表xi的邻居，Ni代表落入像素xi周围窗口的邻居集合。 参数a用于控制邻居项的效果。 根据定义，每个采样点xi满足SUMc(uji) = 1的约束。
隶属度划分矩阵和聚类中心的计算如下：

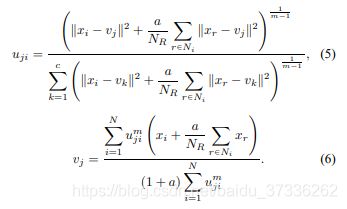
（6）的分子中的第二项1 / NR *r∈Ni（xr）实际上是窗口内xi附近的邻居平均灰度值。 由图像像素周围的所有相邻平均值组成的图像形成所谓的均值滤波图像。
Chen和Zhang [12]提出了FCM_S1，它是FCM_S，其中邻域项的表示更加简化。 目标函数编写如下：

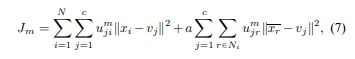
其中，xr_average是位于xr周围窗口内的相邻像素的平均值。 与（4）不同，由于将（4）中的1 / NR *r∈Ni|| xr-vj || 2替换为|| xr_average-vj || 2，因此可以预先计算xr，从而减少了整个计算时间。 关于μij和vj最小化（7）的迭代算法可以类似于FCM_S，其导出如下：


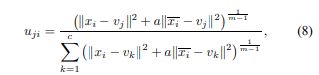
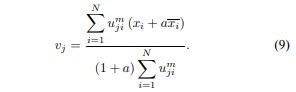
FCM_S1的本质是使原始图像和相应的均值滤波图像具有相同的原型或聚类结果。 此外，FCM_S1不仅大大减少了执行时间，而且提高了对高斯噪声的鲁棒性[12]。
但是，FCM_S1不适合被脉冲噪声破坏的图像[12]。 为了克服这个问题，Chen和Zhang [12]设计了FCM_S2，这是FCM_S1的一种变体，其中均值滤波后的图像被中值滤波后的图像代替。
解决FCM_S，FCM_S1和FCM_S2的目标函数的迭代算法与经典FCM算法中使用的迭代算法大致相同。 应该只替换相应的函数，并且应该在第一次迭代之前计算均值和中值滤波的图像（仅对于FCM S1和FCM S2）。

C.增强的模糊C均值聚类（EnFCM）

Szilagyi等人[13]提出了EnFCM算法来加快灰度图像的聚类过程。 为了加速FCMS，预先从原始图像及其局部邻域均值图像形成线性加权和图像ξ。

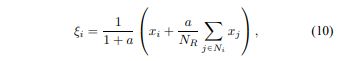
其中ξi表示图像ξ的第i个像素的灰度级值，Ni代表落入xi周围的窗口的一组邻居（xj）。 参数a起到与以前相同的作用，即控制邻居项的效果。 然后，对新生成的图像ξ的灰度直方图执行聚类方法[13]。 因此，在这种情况下，目标函数定义为：

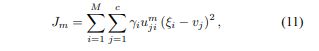
其中vj表示第j个聚类的原型，uji表示相对于聚类j的灰度值i的模糊隶属关系，M表示图像ξ的灰度级数量，通常比N小得多，而γi为 灰度值等于i的像素数。 因此，sum（γk）= N且在任何i的sum（uji）= 1的约束下，使用以下等式计算隶属度分配矩阵和聚类中心，将Jm（11）最小化：

EnFCM算法的迭代过程类似于FCM，但是通过使用（12）和（13）将其应用于新图像ξ（10）。
由于像素的灰度级值通常以8位分辨率（256灰度级）进行编码，因此灰度级数M通常比图像的大小N小得多。 因此，执行时间显着减少。
EnFCM可以提供与FCM S相当的分割结果，但是分割质量取决于所选的窗口大小，参数a和过滤方法。 如果将参数a选择得足够大，则该方法具有抗噪性，但是，另一方面，如果将a选择得足够小，则分割后的图像将保持其清晰度和细节。 但是，当没有关于图像噪声的先验知识时，参数a的选择不是一件容易的事，必须根据经验或使用试错法进行选择。

D.快速广义模糊C均值聚类（FGFCM）

Cai等[16]提出了一种快速广义模糊c均值（FGFCM）算法，以改善聚类结果，并方便选择相邻的控制参数。 为了改善聚类结果，FGFCM利用局部相似性度量将空间和灰度图像信息结合在一起，包括：

其中第i个像素是局部窗口的中心，第j个像素表示在第i个像素周围落入窗口的邻居的集合。 （pi，qi）是像素i的坐标，而xi是像素的灰度值。 λs和λg是两个比例因子，其作用类似于EnFCM中的因子a，σi定义为：

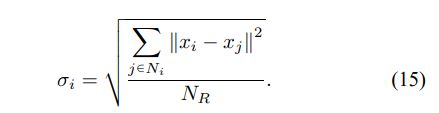
FGFCM将局部和灰度级信息（14）合并到其目标函数中，从而预先生成新图像ξ，如下所示：

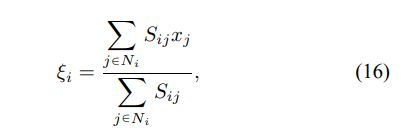
其中ξi表示图像ξ的第i个像素的灰度值，xj表示xi（窗口中心）的邻居的灰度值，Ni是落入局部窗口的邻居的集合，Sij是局部的 第i个像素和第j个像素之间的相似性度量。
此外，Cai等人[16]提出了FGFCM算法的两个变体，即FGFCM S1和FGFCM S2，它们在目标功能上纳入了改进的相似性度量。 FGFCM S1对所有i和j使用Sij = 1，并且自然ξi等于指定窗口（包括第i个像素）内邻居的均值。 另一方面，FGFCM S2使用Sij = median {xj}作为相似性度量，即ξi是指定窗口（包括第i个像素）内邻居的中位数。
FGFCM算法可以总结如下：
1）设定c，m和ε的值，
2）根据（16）计算新图像ξ，
3）初始化模糊分区矩阵U
（0），并设置循环计数器b = 0，
4）使用（13）更新聚类中心v（b）j：
5）使用（12）更新隶属度矩阵U（b + 1）：
6）如果max {U（b）− U（b + 1）} <ε，则停止，否则设置
b = b +1并转到步骤4。
与EnFCM算法一样，执行时间的显着减少归因于考虑了给定图像的灰度级分布范围。
FGFCM及其变体可提供足够好的分割结果，但分割质量取决于所选的窗口大小以及参数λs和λg。 参数λs可以固定为3 [16]。 因此，参数λg控制算法。如果λg的被选择足够大的，则该方法是将抗噪声，但在另一方面，当被选择λg的足够小的分段图像保持其锐度和细节。 但是，由于没有关于图像噪声的先验知识，因此选择参数λg并非易事，必须根据经验或通过试错法进行选择。

三， 模糊局部信息C均值（FLICM）聚类算法

基于FCM S1，FCM S2，EnFCM和FGFCM及其变体的个体优势，在本文中，我们提出了一种新颖而强大的图像聚类FCM框架，称为模糊局部信息C均值（FLICM）聚类算法。

A.介绍模糊因子G

上一节中描述的所有方法都对图像[12]，[13]，[16]产生了有效的聚类结果，但是仍然存在一些缺点：1）尽管引入了局部空间信息在一定程度上增强了它们对噪声的不敏感度 ，它们仍然缺乏足够的鲁棒性[18]，[19]，[20]来抵抗噪声和离群值，尤其是在缺乏对噪声的先验知识的情况下； 2）在它们的目标函数中有一个关键参数a（或λ），用于在对噪声的鲁棒性和保留图像细节的有效性之间取得平衡。 通常，必须通过经验或反复试验来选择它。 3）它们都应用在静态图像上，必须事先计算。 原始图像的细节可能会丢失，具体取决于生成新图像的方法。
为了克服上述缺点，需要FCM目标函数中的新因素。 新因素应具有一些特殊特征：
•以模糊方式合并本地空间和本地灰度信息，以保持鲁棒性和对噪声不敏感。
•根据邻近像素与中心像素的距离来控制邻近像素的影响。
•使用原始图像，以避免可能导致细节丢失的预处理步骤。
•没有任何参数选择。
因此，我们介绍了新颖的模糊因子Gki，其定义为：

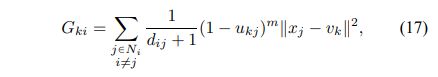
其中第i个像素是局部窗口的中心（例如3×3），k是参考簇，第j个像素属于落入第i个像素周围的窗口的邻居集合 （Ni）。 di，j是像素i和j之间的空间欧几里得距离，ukj是第k个聚类中第j个像素的隶属度，m是每个模糊隶属度的加权指数，而vk是像素的原型群集k的中心。
不难看出，因子Gki完全不使用任何控制图像噪声和图像细节之间平衡的参数。通过定义每个图像像素（空间和灰度）的模糊性，可以自动实现对这种平衡的控制。另外，通过使用dij，因数Gki使局部窗口内的像素的影响根据其距中心像素的距离灵活地变化。因此，可以使用更多的局部空间信息。值得指出的是，在我们的实验中使用的局部窗口的形状是正方形，但是，其他形状（例如菱形或圆形）的窗口也可以轻松地应用于算法。总体而言，Gki反映了邻居的衰减程度以及与中心像素的空间距离。相反，将FCM_S，EnFCM，FGFCM及其变体中的参数a（或λ）全局取为常数，因此很难随不同的空间位置或距中心像素的距离而自适应地变化。而且，不需要预处理步骤来应用该算法，如下所示。在下面的小节中还将显示Gki在算法应用中的重要作用。

B. FLICM的总体框架

通过使用Gki的定义，我们现在为图像聚类提出了一个健壮的FCM框架，称为模糊局部信息C均值（FLICM）聚类算法。 它将本地空间和灰度信息合并到其目标函数中，该函数的定义如下：

对于uki和vk，Jm处于其局部极小值的两个必要条件如下：

因此，FLICM算法如下所示：
步骤1.设置聚类中心的数量c，模糊化参数m和停止条件ε。
步骤2.随机初始化模糊分区矩阵。
步骤3.设置循环计数器b = 0。
步骤4.使用（20）计算聚类原型。
步骤5.使用（19）计算成员资格值。
步骤6.如果max（U（b）-U（b + 1））<ε，则停止，否则，设置b = b + 1并转到步骤4。
当算法收敛时，进行去模糊处理，以将模糊分区矩阵U转换为明快分区。 最大隶属度过程是已开发的对分区矩阵U进行去模糊处理的最重要方法。此过程将像素i分配给具有最高隶属度的C类：

它用于将所提出的算法获得的模糊图像转换为清晰的分割图像。
FLICM目标函数（18）中使用的度量仍然是FCM中的欧几里得度量，其计算简单。 此外，与FCM不同，FLICM具有鲁棒性，因为引入了因子Gki，可以分析如下：
耐噪声性和离群值抗性完全依赖于Gki的定义，如在（18）中所见。 即使没有任何先验的噪声知识，也会自动确定Gki而不是人为设置。 下面将介绍两个基本情况，这些情况描述了窗口中存在异常值时的算法性能。 如将显示的那样，忽略噪声的影响，窗口内受噪声破坏的像素的Gki值将保持与中心像素相似的值。 Gki值将在每次迭代中自适应地变化，收敛到中心像素的值，从而保持对噪声和离群值的不敏感度：

• 情况1：中心像素不是噪点，其局部窗口内的某些像素可能会被噪点破坏。图1所示的示例描述了这种情况，其中使用了3×3的窗口。该窗口是从图1顶行左侧所示的嘈杂图像（标有矩形）中提取的。清楚地显示，经过五次迭代，算法收敛，并且相应的嘈杂成员值以及无噪声像素的收敛到一个相似的值，忽略了有噪声像素（图1（a）-1（d））。还检查了相邻像素，在这些像素中相应的窗口被相互覆盖。通常，在这种情况下，带噪像素的灰度值与窗口内的其他像素相差很大，因此因子Gki平衡了它们的隶属度值。因此，合并在Gki中的空间和灰度约束的组合抑制了噪点像素的影响，因此该算法对异常值变得更加健壮。
• 情况2：中心像素被噪声破坏，而其局部窗口内的其他像素是同质的，未被噪声破坏。 在图2中清楚地展示了这样的示例。再次使用了3×3窗口，该窗口是从图2顶部左侧所示的嘈杂图像（标有矩形）中提取的。 经过5次迭代，有噪（中央）像素的隶属度值收敛到与相邻像素相似的隶属度值，从而忽略了噪声的潜在影响，如图2（d）所示。 通常，在这种情况下，因数Gki以模糊的方式平衡考虑了空间以及无噪声相邻像素的灰度级的中心像素的隶属度。 因此，由于中心像素的隶属度值不受噪声影响，因此所提出的方法对异常值变得更加鲁棒。