dbscan算法中 参数的意义_DBSCAN算法及sklearn实现
基本概念:(Density-Based Spatial Clustering of Application with Noiso)
1.核心对象:
若某个点的密度达到算法设定的阈值则其为核心点。(即r领域内的点数量不小于minPts)
2.ε-领域的距离阈值:
设定的半径r
3.直接密度可达:
若某点p在点q的r领域内,且q是核心点则p-q直接密度可达
4.密度可达:
若有一个点的序列q0、q1、 ...qk,对任意qi-qi-q是直接密度可达的,则称从q0到qk密度可达,这实际上是直接密度可达的"传播"。
5.密度相连:
若从某核心点p出发,点q和点k都是密度可达的,则称点q和点k是密度相连的
6.边界点:
属于某一类的非核心点,不能发展下线了
7.直接密度可达:
若某点p在点q的r领域内,且q是核心点则p-q直接密度可达
8.噪声点:
不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
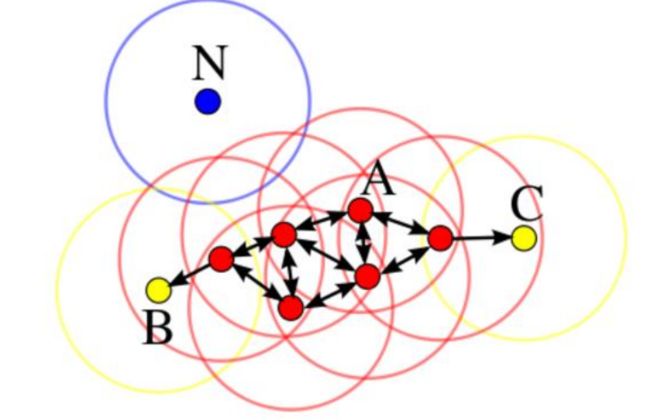
9.可视化展示:
A:核心对象
B,C:边界点
N:离群点
工作流程:
参数D:
输入数据集
参数ε:
指定半径
MinPts:
密度阈值
半径ε,可以根据K距离来设定:找突变点
K距离:
给定数据集P={p(i);i=0,1...n},计算点P(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。
MinPts:
k-距离中的k值,一般取得小一些,多次尝试,这儿有个聚类可视化好玩的网址点击这里,可以感受下,挺好玩的。
优势:
不需要指定簇个数
可以发现任意形状的簇
擅长找到离群点(检测任务)
劣势:
高维数据有些困难(可以做降维)
参数难以选择(参数对结果影响非常大)
Sklearn中效率很慢(数据消减策略)
kmeans-dbcan聚类对比
#beer dataset
importpandas as pd
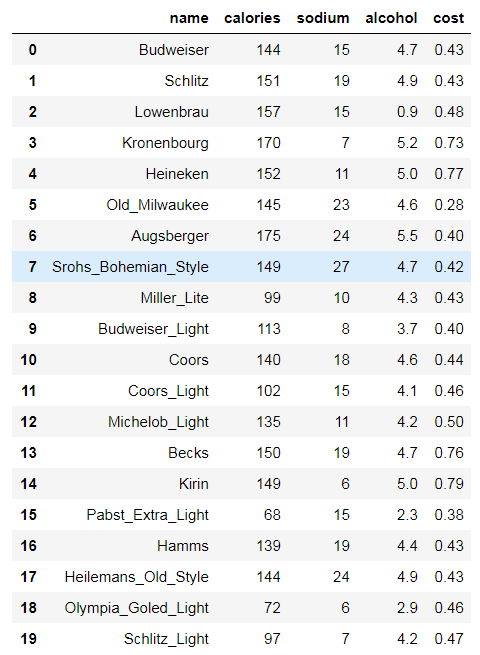
beer= pd.read_csv('data.txt', sep=' ')
beer
X = beer[["calories","sodium","alcohol","cost"]]
# K-means clustering
from sklearn.cluster importKMeans
km= KMeans(n_clusters=3).fit(X)
km2= KMeans(n_clusters=2).fit(X)
km.labels_
array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 2, 0, 0, 2, 1])
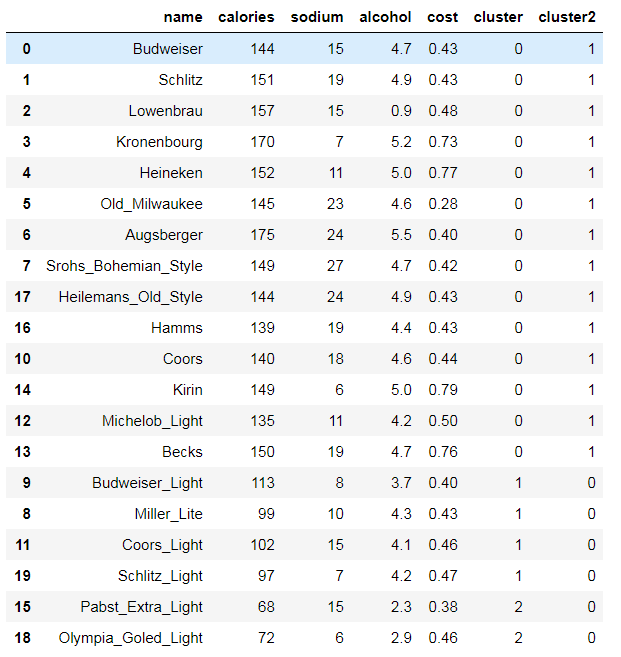
beer['cluster'] =km.labels_
beer['cluster2'] =km2.labels_
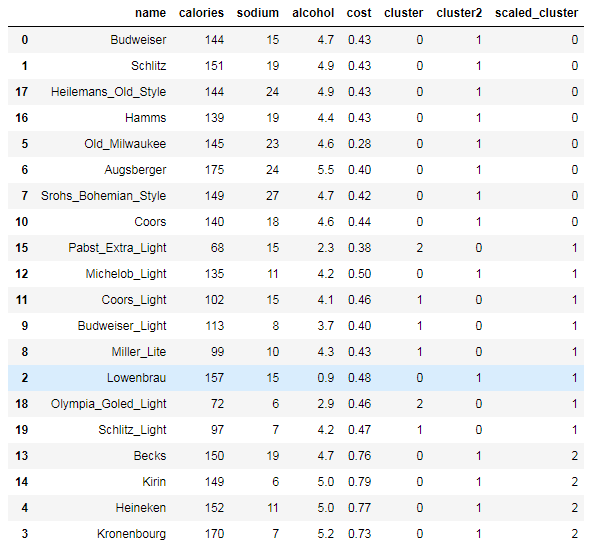
beer.sort_values('cluster')
from pandas.tools.plotting importscatter_matrix%matplotlib inline
cluster_centers=km.cluster_centers_
cluster_centers_2= km2.cluster_centers_
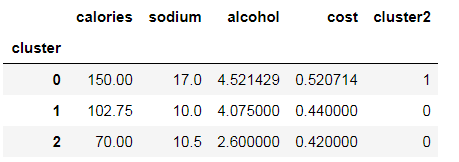
beer.groupby("cluster").mean()
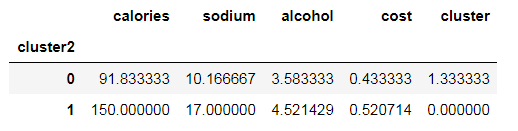
beer.groupby("cluster2").mean()
centers = beer.groupby("cluster").mean().reset_index()
%matplotlib inlineimportmatplotlib.pyplot as plt
plt.rcParams['font.size'] = 14
importnumpy as np
colors= np.array(['red', 'green', 'blue', 'yellow'])
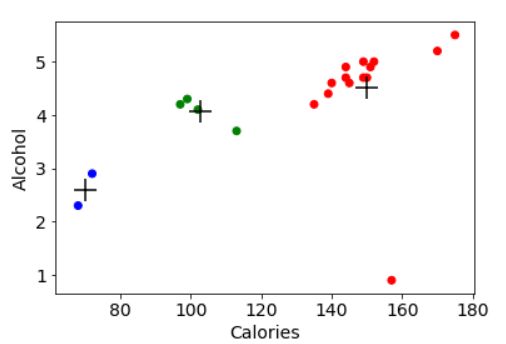
plt.scatter(beer["calories"], beer["alcohol"],c=colors[beer["cluster"]])
plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')
plt.xlabel("Calories")
plt.ylabel("Alcohol")
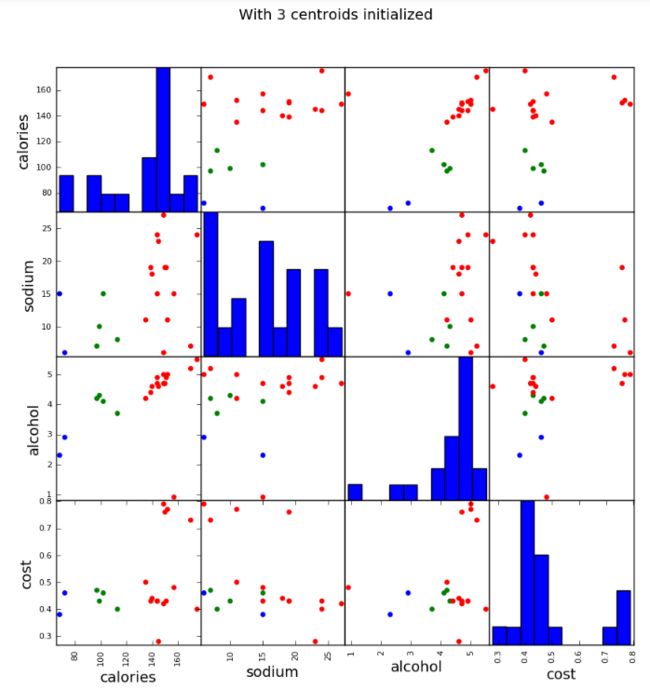
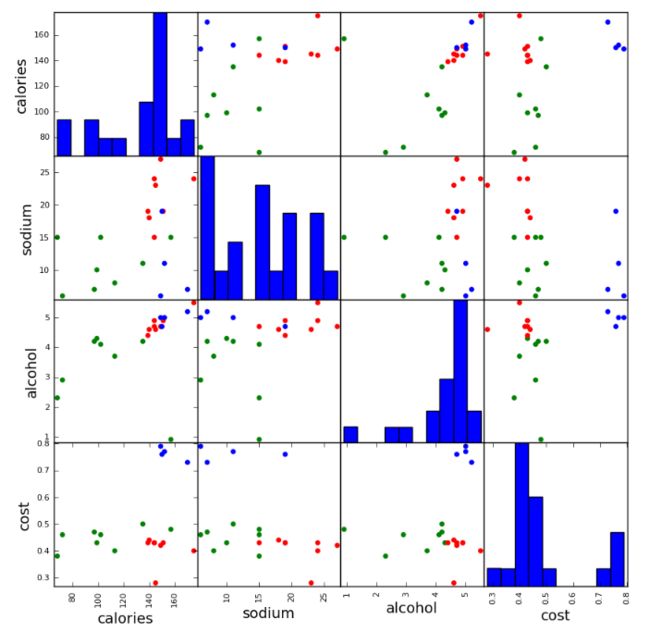
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster"]], figsize=(10,10))
plt.suptitle("With 3 centroids initialized")
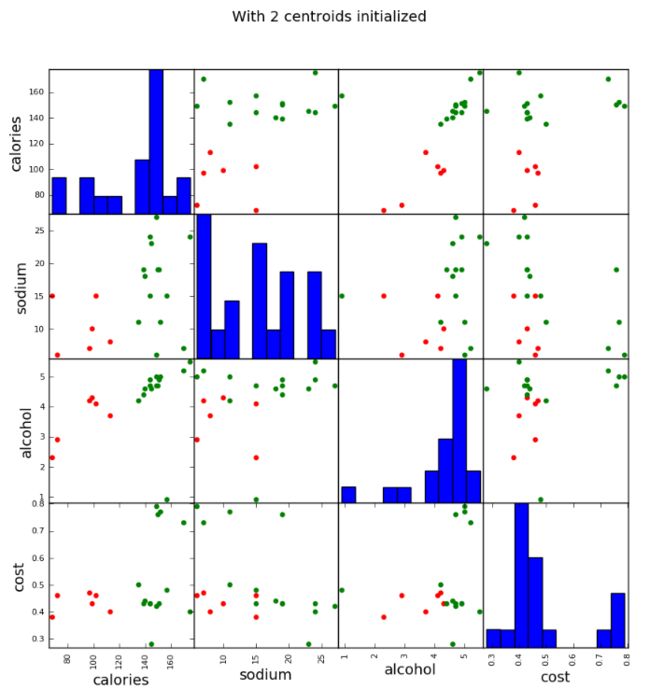
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster2"]], figsize=(10,10))
plt.suptitle("With 2 centroids initialized")
from sklearn.preprocessing importStandardScaler
scaler=StandardScaler()
X_scaled=scaler.fit_transform(X)
X_scaled
array([[ 0.38791334, 0.00779468, 0.43380786, -0.45682969],
[ 0.6250656 , 0.63136906, 0.62241997, -0.45682969],
[ 0.82833896, 0.00779468, -3.14982226, -0.10269815],
[ 1.26876459, -1.23935408, 0.90533814, 1.66795955],
[ 0.65894449, -0.6157797 , 0.71672602, 1.95126478],
[ 0.42179223, 1.25494344, 0.3395018 , -1.5192243 ],
[ 1.43815906, 1.41083704, 1.1882563 , -0.66930861],
[ 0.55730781, 1.87851782, 0.43380786, -0.52765599],
[-1.1366369 , -0.7716733 , 0.05658363, -0.45682969],
[-0.66233238, -1.08346049, -0.5092527 , -0.66930861],
[ 0.25239776, 0.47547547, 0.3395018 , -0.38600338],
[-1.03500022, 0.00779468, -0.13202848, -0.24435076],
[ 0.08300329, -0.6157797 , -0.03772242, 0.03895447],
[ 0.59118671, 0.63136906, 0.43380786, 1.88043848],
[ 0.55730781, -1.39524768, 0.71672602, 2.0929174 ],
[-2.18688263, 0.00779468, -1.82953748, -0.81096123],
[ 0.21851887, 0.63136906, 0.15088969, -0.45682969],
[ 0.38791334, 1.41083704, 0.62241997, -0.45682969],
[-2.05136705, -1.39524768, -1.26370115, -0.24435076],
[-1.20439469, -1.23935408, -0.03772242, -0.17352445]])
km = KMeans(n_clusters=3).fit(X_scaled)
beer["scaled_cluster"] =km.labels_
beer.sort_values("scaled_cluster")
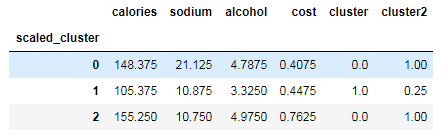
beer.groupby("scaled_cluster").mean()
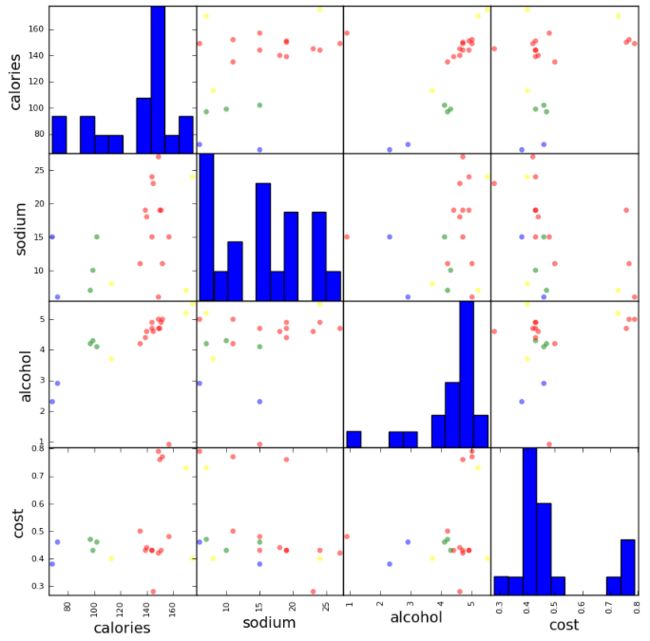
pd.scatter_matrix(X, c=colors[beer.scaled_cluster], alpha=1, figsize=(10,10), s=100)
from sklearn importmetrics
score_scaled=metrics.silhouette_score(X,beer.scaled_cluster)
score=metrics.silhouette_score(X,beer.cluster)print(score_scaled, score)
scores =[]for k in range(2,20):
labels= KMeans(n_clusters=k).fit(X).labels_
score=metrics.silhouette_score(X, labels)
scores.append(score)
scores
[0.69176560340794857,0.67317750464557957,0.58570407211277953,0.42254873351720201,0.4559182167013377,0.43776116697963124,0.38946337473125997,0.39746405172426014,0.33061511213823314,0.34131096180393328,0.34597752371272478,0.31221439248428434,0.30707782144770296,0.31834561839139497,0.28495140011748982,0.23498077333071996,0.15880910174962809,0.084230513801511767]
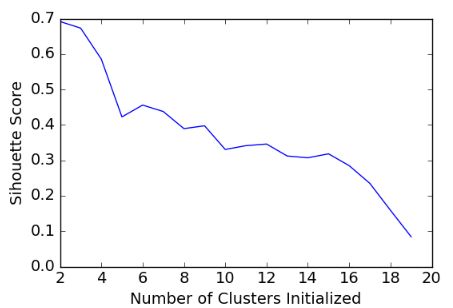
plt.plot(list(range(2,20)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")
# DBSCAN clustering
from sklearn.cluster importDBSCAN
db= DBSCAN(eps=10, min_samples=2).fit(X)
labels = db.labels_
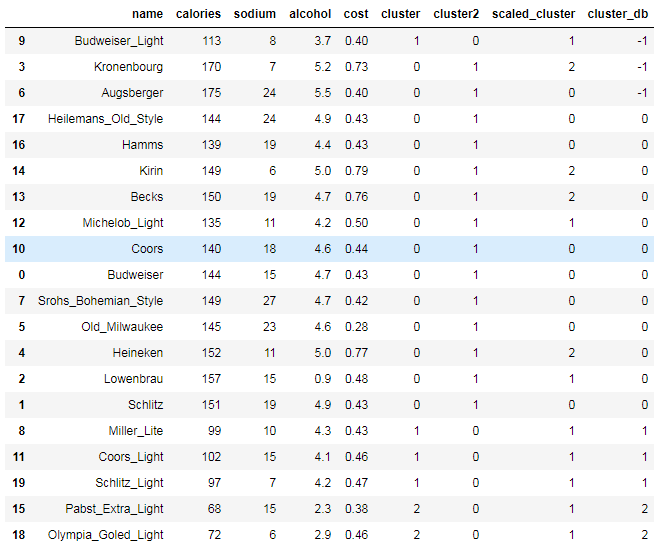
beer['cluster_db'] =labels
beer.sort_values('cluster_db')
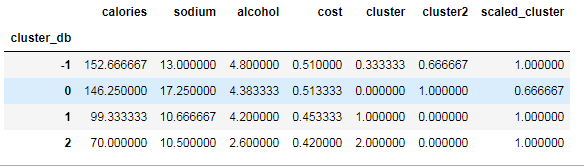
beer.groupby('cluster_db').mean()